石以砥焉，化钝为利——突破《平行线的性质》学习难点的教学探索

福建省厦门一中海沧分校(361026) 王旭辉 ●

石以砥焉，化钝为利
——突破《平行线的性质》学习难点的教学探索

福建省厦门一中海沧分校(361026) 王旭辉 ●

《平行线的性质》是初中几何学习中的一个基础内容，也是重要内容．但因此节内容中公理、定理较多，且学生刚刚接触“几何说理”，更增加了学习的难度．但在教学中，只要能够从学生的兴趣入手，在课堂教学中，始终把握新课程精神，充分运用“小组合作”、“主动探究”等教学方法，就能突破《平行线的性质》学习难点，取得良好的教学成效．

平行线的性质;合作;探究

一、知之不如好之——兴趣导入，激发求知

俗话说:兴趣是最好的老师．要想在难度相对大一些的内容教学中，取得较好的教学效果，激发起学生的兴趣，是很重要的一步．初中数学新课程标准中也指出:“学生的数学学习内容应当是现实的、有意义的、富有挑战性的，这些内容要有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动．”由此可见，以兴趣导入新课教学，以激发学生主动进行学习，对提高课堂教学效果有着重要意义．

例如，在新课导入环节，笔者结合学生的生活实际，进行了如下的教学设计:

已知:公路c分别与两条互相平行的公路a，b相交，两辆汽车在公路a，b上同向行驶拐弯后上公路c又同向行驶．

(1)如果公路c与公路a的交角为70°，那么公路c与公路b的交角是多少度呢?

(2)如果两条直线平行，同位角，内错角，同旁内角各有什么关系呢?

这样利用生活中的实际问题导入，引出新问题，为学生将新知识纳入自己的认知体系做好铺垫，使学生认识到数学知识来源于生活，应用于生活，激发他们的求知欲望．

二、在分享中学习——主动参与，探究合作

初中数学新课程标准提倡“探索并主动参与特定的数学活动，通过观察、实验、推理等活动发现对象的某些特征或与其他对象的区别和联系．”因此，在教学实践中，要充分发挥学生的主体作用，让他们主动参与课堂活动，通过小组合作等方式进行探究．这也符合新课标提出的“学会与人合作”的要求．在平行线性质的教学中，平行线性质的探索过程是这节内容中最突出的环节．

(一)小组探究，学习重点

笔者事先让学生准备好白纸，三角板，在上课时学生通过自主画图进行探索，得到猜想，再通过验证发现的．即在学生充分活动的基础上，由学生自己发现问题的结论，让学生感受成功的喜悦，增强学习的兴趣和学习的自信心．在探究“两直线平行，同位角相等”时，要求全体学生参与，体现了新课程理念下的交流与合作．

笔者先让同学利用手中的方格纸，任意选取其中的两条线作直线，再随意画一条直线与这两条平行线相交，并标注一些角．如图．

然后，组织学生开展小组活动．

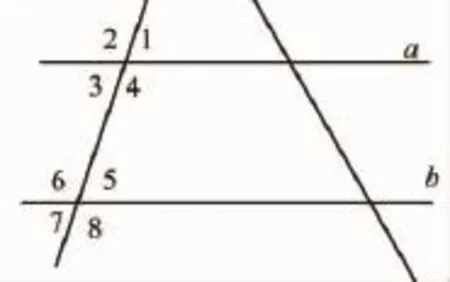
数学新课标提出:“经历观察、操作、归纳等学习数学的过程，感受数学思考过程的合理性．”为了让学生亲历数学活动过程，提高教学的实效性，笔者让其中一个小组对上图中的八个角进行度量，并把度量结果填入下表:

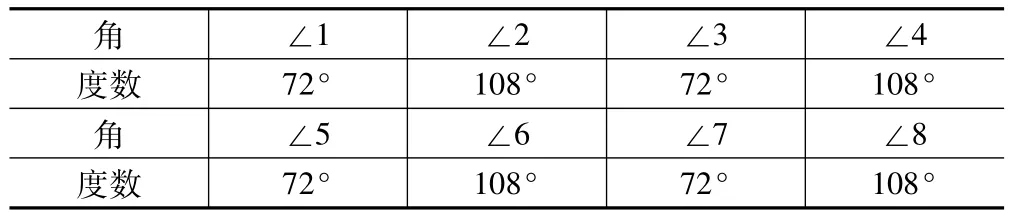
_____角∠1 ∠2 ∠3 ∠4____ ____度数___ _________72° 108° 72° 108° _____角∠5 ∠6 ∠7 ∠8____ ____度数 72° 108° 72° 108°

新课标提出，“在独立思考的基础上，积极参与对数学问题的讨论，敢于发表自己的观点”．所以，为了让学生能够积极参与到数学问题讨论中来，笔者让学生根据上述表中数据进行讨论:各对角的度数有什么关系?写出猜想:两平行线被第三条直线所截，同位角___、内错角___、同旁内角___．

在此基础上，为了使得出的结论得到进一步强化，让各小组同学再任意画一条截线同样度量并计算各角的度数，表达猜想．

在这样的教学活动中，学生通过动手实践，观察分析，合理猜想，合作交流，解决以上三个问题，体验并感悟平行线性质，使学生感受到学习的快乐，真正成为学习的主人，这对于发展学生的空间观念理解平行线性质是十分重要的，也达到突出重点、突破难点的目的．

(二)展开讨论，突破难点

初中数学新课程标准提出:“对不懂的地方或不同的观点有提出疑问的意识，并愿意对数学问题进行讨论．”要想使学生对知识能够在短时间内熟练掌握，其中一个重要方法，就是让学生充分讨论．对于平行线的性质定理与判定定理，是初学者最容易混淆的内容，学生难以分清哪是判定定理，哪是性质定理．为了让学生能够区分平行线的性质定理与判定定理，提出了如下问题:平行线性质与前面所学的判定定理有什么不同?经过同桌之间、小组内讨论交流之后，学生发言踊跃，纷纷举手表达结论，从而使得此节内容的难点内容得以突破．

三、熟读而精思——巩固创新，理性升华

初中数学新课程标准提出，对学生的培养目标是“具有初步的创新精神和实践能力”．而要实现这一目标，就需要把知识内化为学生的能力，还需要进一步的练习．只有让学生在练习中思考，在思考中进步，学生的创新思维才能得到发展，学生的创新能力也才能得到培养．

(一)引导思考，发展思维

说理、推理是本章的教学重点，也是本节的一个教学难点．为突破难点我先有意识地留一些空白，让学生填写推导出的结论，填出得出结论的理由，这样安排也是循序渐进地引导学生思考，使学生初步养成言之有理的习惯，从而能逐步进行简单的推理．

例如，在学完平行线性质定理后，笔者设计了如下几个小问题:

(1)你能根据性质1，说出性质2、性质3成立的道理吗?

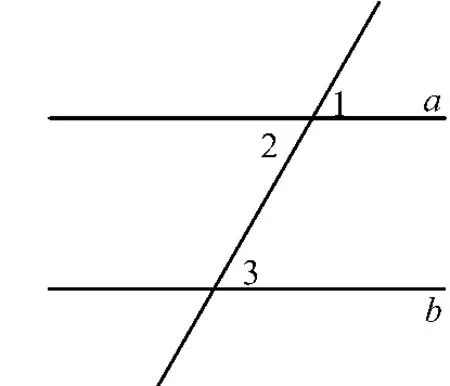
(2)如图，因为a∥b，所以∠1 =∠3( )．

又∠1=___( )，

所以∠2=∠3( )．

(3)类似地，对于性质3，你能说出道理吗?

(二)例题学习，培养能力

为了进一步培养学生的能力，在学习了平行线的性质定理后，笔者精心选择了下面两个例子:

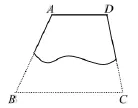
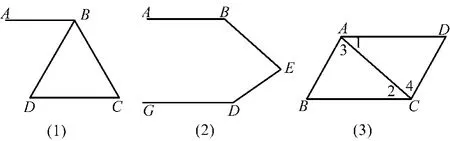
例1 如图是一块梯形铁片的残余部分，量得∠A= 115°、∠D=100°，梯形另外两个角是多少度?

先由教师引导提问:

1，由梯形定义能得出哪两条线段平行?(AD∥BC)

2，由平行线的性质能得出什么结论?(∠A+∠B=180°，∠D+∠C=180°)

再由学生用几何语言进行表达，初次计算格式不一定很完整，要给学生一定的鼓励和肯定．

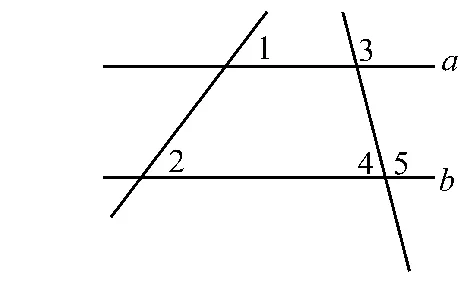
例2 如图，∠1=50°、∠2 =50°、∠3=100°，求∠4的度数．分析时，笔者采用的是从问题入手:求∠4←求∠5←a∥b←∠1=∠2．

让学生初步体会几何题的推理方法，逐渐提高他们的推理能力，接下来引导学生写出推理过程．

(三)巩固练习，知识升华

学习离不开练习，学习离不开强化．为了不断强化所学知识，做到让学生对所学知识记忆长久，需要坚持“循序渐进”的原则，不断加以练习．

一方面，可以设计趣味练习，寓教于乐，进一步让学生感受知识来源于实践．选取练习题目时，要以紧扣基础，提高灵活运用定理的能力为原则，以突出重点、突破难点，并进一步提高用符号语言进行推理的能力．

例如，一辆汽车在公路上行驶，在两次转弯后，仍在原来的方向上平行行驶，那么这两次转变的角度可以是( )．

A．先右转80°，再左100° B．先左转80°，再右转80°

C．先左转80°，再左转100°D．先右转80°，再右80°

另一方面，可以设计强化练习．例如:

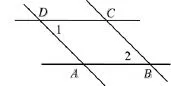
1．如图，已知AB∥CD，AD∥BC，判断∠1与∠2是否相等，并说明理由．

2．如图，已知∠ABC+∠C=180°，BD平分∠ABC，∠CBD与∠D相等吗?请说明理由．

3．如图，已知AB∥CD，∠B=140°，∠D=150°，求∠E的度数．

4．如图，已知AB∥CD，下列解答过程是否正确:

解 ∵ AB∥CD(已知)，

∴∠1=∠2(两直线平行，内错角相等)．

∠BAD+∠B=180°(两直线平行，同旁内角互补)．

总之，在《平行线的性质》教学中，只要教师能够从学生的兴趣入手，始终把握新课程精神，充分运用“小组合作”、“主动探究”等教学方法，就能突破《平行线的性质》学习难点，实现“石以砥焉，化钝为利”，从而取得良好的教学成效．

［1］教育部．全日制义务教育数学课程标准［M］．北京:北京师范大学出版社，2001．

［2］陈明华．中学数学课堂教学如何改革与创新［M］．成都:四川大学出版社，2004．

G632

B

1008－0333(2017)02－0027－02