特殊位置作用大

江苏省淮安市淮阴区开明中学(223300) 马先龙 ●

特殊位置作用大

江苏省淮安市淮阴区开明中学(223300) 马先龙 ●

解几何最值问题时，若能捕捉图形的特殊位置，利用特殊位置时的图形解题，往往能化难为易，事半功倍．

一、与三角形有关的问题

例1 如图1，在△ABC中，∠ACB=90°，∠ABC= 30°，将△ABC绕顶点C顺时针旋转，旋转角为α(0°＜α＜180°)，得到△A'CB'．设AC中点为M，A'B'中点为N，AC= 2，连接MN，则线段MN 的最大值为___．

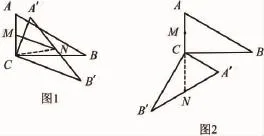
分析 如图2，当△ABC绕顶点C顺时针旋转到M、C、N三点共线时，即是本题的特殊位置图形．此时，CM+ CN就是MN的最大值．

解 如图1，在Rt△ABC中，∵∠ACB=90°，∠ABC= 30°，AC=2，∴AB=4．连结 CN，在 Rt△A'B'C中，∵∠A'CB'=90°，N为A'B'中点，∴此时CM、CN不共线，有MN＜CM+CN;如图2，当CM、CN共线时，有MN=CM+CN，∴MN≤CM+CN．∵M为AC的中点，∴3，∴MN的最大值为3．

二、与四边形有关的问题

例2 如图3，正方形ABCD中，AB=2，动点E从点A出发向点B运动，同时，动点F从点B出发向点C运动，点E、F运动的速度相同，当它们到各自终点时停止运动．设运动过程中AF与DE相交于点M，P是边CD上任意一点，则PB+PM 的最小值为___．

分析 如图4，当动点E运动到点B，动点F运动到点C，即是本题的特殊位置图形．此时，作点B关于CD的对称点B'，连接B'M交CD于点P，则B'M就是PB+PM的最小值．

解 如图4，当点E、F分别运动到点B、C时，M是正方形ABCD的对角线AC、BD的交点，作点B关于CD的对称点B'，连接B'M与CD相交于点P，则B'M就是PB+ PM的最小值．过点M作MN⊥BC于点N，在Rt△B'MN中，∵∠B'NM=90°，MN=1，B'N=2+1=3，∴B'M=PB+PM的最小值为

三、与圆有关的问题

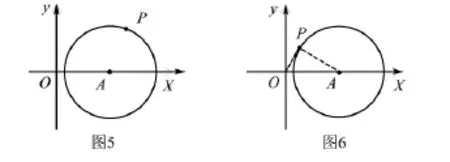
分析 如图6，当OP与⊙A相切时，即是本题的特殊位置图形．此时，∠POA最大，从而tan∠POA最大，而tan∠POA，故此时最大，据此即可求出的最大值．，故此时最大．连接AP，∵OP是⊙A的切线，∴∠OPA=90°．∵A(2，0)，∴OA=2．在Rt△AOP中，∠OPA=90°，OA=2，AP=

解 如图6，连接OP，当OP与⊙A相切时，∠POA最大，从而tan∠POA最大．∵的最大值为的最大值为

例4 如图7，△ABC是边长为3的等边三角形，M是边BC上的一个动点，以AM为直径画⊙O分别交AB，AC于点P，Q，连结PQ，则线段PQ 的最小值为____．

解 如图7，作直径PR，连接QR，则∠PQR=90°，∠PRQ=∠BAC=60°．在Rt△PRQ中，∠PQR=90°，．过点A作AH⊥BC，垂足为点H，则AH就是AM的最小值．在Rt△ABH中，∠AHB=90°，∠ABH=60°，AB的最小值为线段PQ的最小值为线段PQ的最小值为

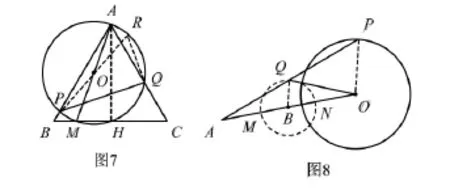
例5 如图8，已知A是⊙O外一点，P是⊙O上的动点，线段AP的中点为Q，连接AO，OQ．若⊙O的半径为2，OA=5，则线段OQ 的最大值是___．

分析 如图8，取OA的中点B，连接BQ，OP，易知BQ =1，点Q是半径为1的⊙B上的动点．设AO与⊙B相交于M、N，则OM就是OQ的特殊位置图形，据此可求出OQ的最大值．

解 如图8，取OA的中点B，连接BQ，OP．∵Q、B分别为AP、AO的中点，∴BQ为△AOP的中位线OP．∵OP=2，∴BQ=1．以点B为圆心，作半径为1的⊙B，则点Q是⊙B上的动点．设AO与⊙B分别相交于点M、 N，则当点Q运动到点M时，OQ最大线段OQ的最大值是

从以上几例可以看出，认真审题，把握图形本质，弄清运动对象的路径并捕捉到图形的特殊位置是解题成功的关键．一旦捕捉到图形的特殊位置并画出特殊位置时的图形，问题则立刻变得简单了．

G632

B

1008－0333(2017)02－0026－02