半广群C*-代数的一个同构问题

靖杨萍

(杭州电子科技大学理学院，浙江 杭州 310018)

半广群C*-代数的一个同构问题

靖杨萍

(杭州电子科技大学理学院，浙江 杭州 310018)

半广群是范畴的推广，半广群C*-代数不仅包括Cuntz-Krieger代数，而且还包括图C*-代数、高阶图C*-代数等.对于给定的半广群，利用半广群C*-代数的生成元，构造一个新的半广群，并证明2个半广群C*-代数同构.

半广群；半广群C*-代数；同构

0 引 言

Exel R.介绍了半广群C*-代数[1]，其中半广群是范畴的推广.由于半广群C*-代数既包括Cuntz-Krieger代数[2]，也包括图C*-代数、高阶图C*-代数[3-6]、超图C*-代数[7]等，因此半广群C*-代数的研究引起了广大学者的广泛关注.

C*-代数的同构问题是C*-代数相关研究的一个重要内容，本文利用同构理论研究了半广群C*-代数，具有重要的意义.

1 预备知识

定义1.1[1]半广群是一个三元组(Λ,Λ(2),·)，其中Λ是一个集合，Λ(2)是Λ×Λ的子集，·：Λ(2)→Λ是满足以下结合律的运算：如果f,g,h∈Λ使得下列条件之一成立，

(ⅰ)(f,g)∈Λ(2)并且(g,h)∈Λ(2)；

(ⅱ)(f,g)∈Λ(2)并且(fg,h)∈Λ(2)；

(ⅲ)(g,h)∈Λ(2)并且(f,gh)∈Λ(2)；

则(f,g),(g,h),(fg,h),(f,gh)∈Λ(2)并且(fg)h=f(gh).此外，对所有的f∈Λ，设Λf={g∈Λ:(f,g)∈Λ(2)}.

定义1.2[1](1)设f,g∈Λ，若下列条件之一成立：

(ⅰ)f=g；

(ⅱ)存在h∈Λ使得fh=g；

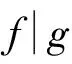
(3)设X是Λ的任意子集，称子集H⊆X是X的一个覆盖，如果对任意f∈X，存在h∈H，使得h∩f.

定义1.3[1]设Λ是一个半广群，B是一个有单位元的C*-代数.映射s:Λ→B被称为Λ在B中的表示，如果对任意的f,g∈Λ，以下4个结果成立：

(ⅰ)sf是一个部分等距；

(ⅲ)如果f⊥g，PfPg=0；

(ⅳ)如果(f,g)∈Λ(2)，QfPg=Pg.

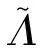
2 主要结果

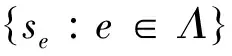
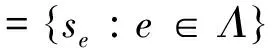
因为(sf,sg)∈Λ′(2)当且仅当(f,g)∈Λ，所以Λ′满足半广群的定义.下面仅证明定义1.1的(ⅰ)，(ⅱ)、(ⅲ)情况类似可证.事实上，如果满足定义1.1的(ⅰ)∶(sf,sg)∈Λ′(2),(sg,sh)∈Λ′(2),由Λ′(2)的定义，可得(f,g)∈Λ(2)，(g,h)∈Λ(2).因为Λ是一个半广群，由定义1.1的(ⅰ)，有(f,g),(g,h),(fg,h),(f,gh)∈Λ(2)并且(fg)h=f(gh).再由Λ′(2)的定义可知，(sf,sg),(sg,sh),(sfg,sh),(sf,sgh)∈Λ′(2).因(sfsg)sh=sf(sgsh)，由定义1.3(ⅱ)可得sfgsh=sfsgh，于是满足定义1.1的结论.

此外，对每一个sf∈Λ′，有

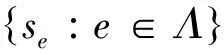
证明 对每一个e∈Λ，设Qe,Pe分别是se的初始投影和终值投影.令

tse=se,Qse=tse*tse,Pse=tsetse*.

容易看出tse是部分等距，且Qse=Qe，Pse=Pe.如果(sf,sg)∈Λ′(2)，则有(f,g)∈Λ(2)，所以，tsftsg=sfsg=sfg=tsfg=tsfsg.

如果(sf,sg)∉Λ′(2)，则有(f,g)∉Λ(2)，所以tsftsg=sfsg=0.

如果(sf,sg)∈Λ′(2)，则有(f,g)∈Λ(2)且QsfPsg=QfPg=Pg=Psg.

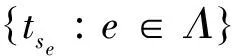
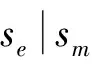
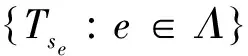
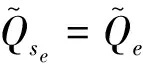
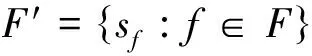
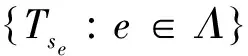
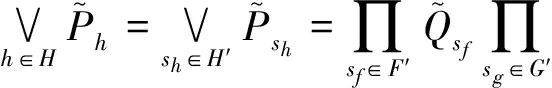
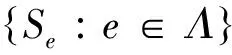
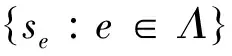
3 结束语

本文介绍了半广群以及半广群C*-代数的概念，此外，对于给定的半广群，利用半广群C*-代数的生成元，构造了一个新的半广群，并证明2个半广群C*-代数是同构的.

[1]EXEL R. SemigroupoidC*-algebras[J]. Journal of Mathematical Analysis and Applications, 2011,377(1):303-318.

[2]EXEL R, LACA M. Cuntz-Krieger algebras for in?nite matrices[J].Reine Angew. Math. 1999,512:119-172.

[3]KUMJIAN A, PASK D. Higher rank graphC*-algebras[J]. New York Journal of Mathematics, 2000,6(1):104-113.

[4]RAEBURN I, SIMS A, YEEND T. Higher-rank graphs and theirC*-algebras[J]. Proceedings of the Edinburgh Mathematical Society, 2003,46(1):99-115.

[5]KUMJIAN A, PASK D, SIMS A. Homology for higher-rank graphs and twistedC*-algebras[J]. Journal of Functional Analysis, 2011,263(6):1539-1574.

[6] HAZLEWOOD R, RAEBURN I, SIMS A, et al. On some fundamental results about higher-rank graphs and theirC*-algebras[J]. Proceedings of the Edinburgh Mathematical Society, 2013,56(2):575-597.

[7]JING Y P. SemigroupoidC*-algebras and ultragraphC*-algebras[J]. Israel Journal of Mathematics, 2015,209(2):593-610.

An Isomorphism of SemigroupoidC*-algebras

JING Yangping

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

SemigroupoidsC*-algebra is a generalization of a category, which include not only theC*-algebras of Cuntz-Krieger, but also the higher-rank graphC*-algebras. Given a semigroupoid, using the generators of SemigroupoidC*-algebra, this paper constructs a new semigroupoid and proves that the two semigroupoidC*-algebras are isomorphic.

semigroupoids; semigroupoidsC*-algebras; isomorphic

10.13954/j.cnki.hdu.2017.02.020

2016-10-18

浙江省教育厅科研资助项目(Y201432224)

靖杨萍(1980-)，女，河南唐河人，讲师，数学.

O177.1

A

1001-9146(2017)02-0092-03