|x|α在调整的Chebyshev结点组的有理插值

许江海,赵 易,蒋银停

(杭州电子科技大学数学研究所，浙江 杭州 310018)

|x|α在调整的Chebyshev结点组的有理插值

许江海,赵 易,蒋银停

(杭州电子科技大学数学研究所，浙江 杭州 310018)

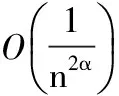
调整的第二类Chebyshev结点；有理插值；Newman-α型有理算子；逼近阶

0 引 言

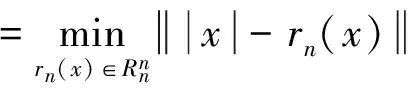
从文献[3]中发现，当所取结点组向零点稠密时，逼近效果更佳.本文用满足这一性质的结点组对|x|α(1≤α<2)做有理函数的逼近，并讨论了逼近阶的大小.

1 rn-1,α(X;x)对|x|α的有理逼近

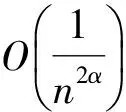
得到了所要讨论的结点组.

根据上述构造的结点组，可以把Newman-α型有理算子定义为

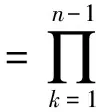
本文得到以下主要结论.

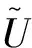
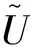
要证明定理1需要如下基本引理.

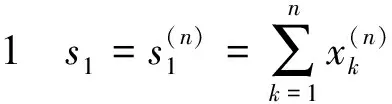
HPLC法同时测定四味姜黄汤散中7种成分的含量…………………………………………………… 赵 娅等（1）： 29

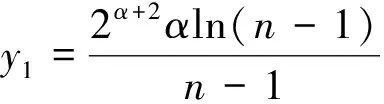
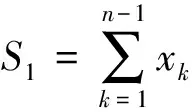
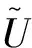
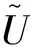
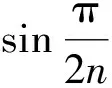
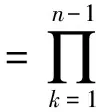
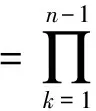
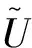
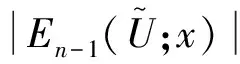
其中C为与n无关的正常数.

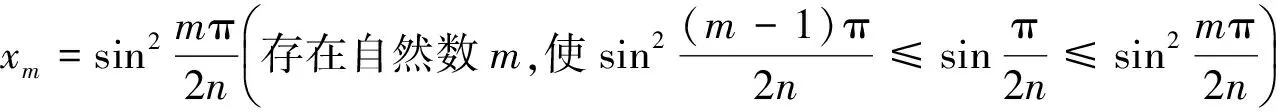
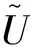
上述不等式中的c为与n无关的正常数，不同位置值可能有所不同.所以有

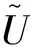
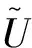
定理1得证.

可以证明定理1中的逼近阶为最优，本文得到以下定理：

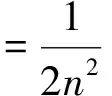
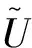
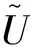
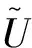
定理2得证.即说明，定理1中的逼近阶不可改进.

2 结束语

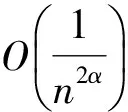
[1]BERNSTEINS.Quelquesremarquessurlinterpolation[J].MathematischeAnnalen, 1918,79(1):1-12.

[5]张慧明，李建俊，段生贵.|x|α在第二类Chebyshev结点的有理插值[J].四川师范大学学报(自然科学版)，2015，38(6):889-892.

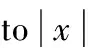
[7]XIA M. On Lagrange interpolation to |x|α(1≤α<2) with equally spaced nodes[J]. Analysis in Theory & Applications, 2004.20(3):281-287.

第37卷第2期

On Rational Interpolation to |x|αat the Adjusted Chebyshev Nodes

XU Jianghai, ZHAO Yi, JIANG Yinting

(InstituteofMathematics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

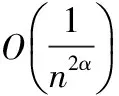
adjusted Chebyshev nodes of the second kind; rational interpolation; Newman-αtype rational operators; order of approximation

10.13954/j.cnki.hdu.2017.02.019

2016-05-25

国家自然科学基金资助项目(11601110)

许江海(1992-)，男，安徽安庆人，硕士研究生，函数逼近论.通信作者：赵易副教授，E-Mail：zhaoyi@hdu.edu.cn.

O174.41

A

1001-9146(2017)02-0089-03