严格半正长方形张量互补问题解的估计

于 雯，凌 晨

(杭州电子科技大学理学院，浙江 杭州 310018)

严格半正长方形张量互补问题解的估计

于 雯，凌 晨

(杭州电子科技大学理学院，浙江 杭州 310018)

针对长方形张量，定义了一个连续正齐次算子和一个常量，证明了长方形张量为严格半正的充要条件是此常量为正.在此基础上，得到了严格半正长方形张量互补问题解的上下界.

张量；长方形张量；严格半正张量；张量互补问题；解的估计

0 引 言

张量互补问题是线性互补问题[1]的推广和非线性互补问题的特例，n人非合作博弈问题可被转化成张量互补模型表述并求解[2].自2014年文献[3]首先提出张量互补问题概念以来，此问题已得到广泛研究，其中，文献[4]讨论了对称正定张量、协正定张量互补问题解的存在性以及可对角化张量互补问题解的唯一性，文献[5]证明了在一定条件下，求解Z-张量互补问题稀疏解可转化成求解一类目标函数为线性的多项式规划问题，文献[6]研究了P-张量互补问题解的性质.长方形张量是更一般的张量，其应用更为广泛.长方形张量的奇异值概念和求解非负长方形张量最大奇异值的交替型算法已由文献[7]给出.与方形张量互补问题相比，长方形张量互补问题需要求两个不同向量，所以其求解更困难.本文研究严格半正长方形张量互补问题解的估计问题.

1 问题描述及预备知识

本文考虑一类长方形张量互补问题:求x∈Rn和y∈Rm，使得:

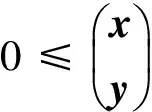
(1)

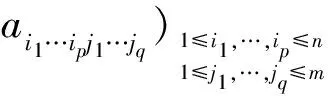
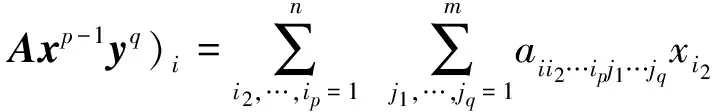
和

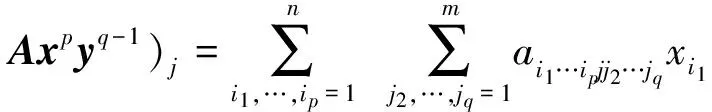
称满足式(1)的(x,y)为长方形张量互补问题的解.

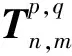
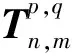
xi(Axp-1yq+c)i+yj(Axpyq-1+d)j>0

(2)

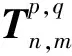
(3)

显然，算子TA连续且为正齐次.进一步，定义TA的无穷范数如下:

(4)

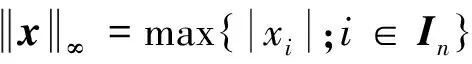
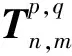
(5)

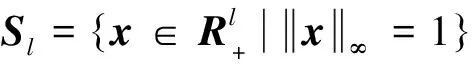
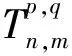
其中dij≥0，则:

1)β(A)≤β(A+D)

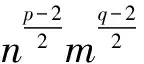
证明 1)因A是严格半正，易知A+D也是严格半正.进一步，由β(A)的定义，知:

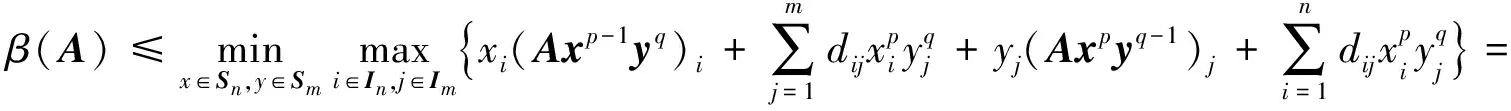
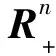
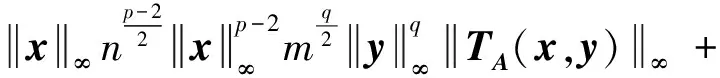
从而有:

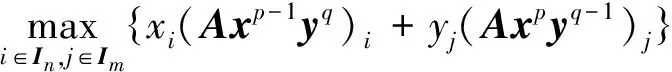
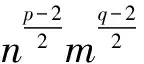
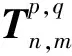
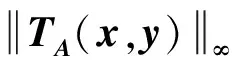
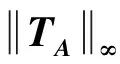
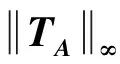
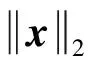
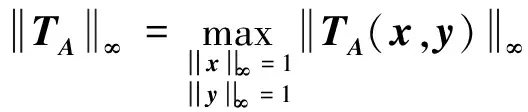
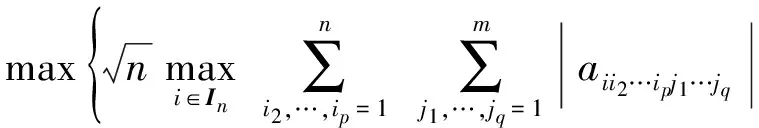
定理1证毕.

2 解的估计

长方形张量互补问题比方形张量互补问题更复杂，其求解更困难.本节研究式(1)解的估计.

2.1 解的上界

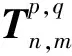
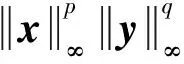
(6)

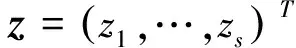
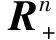
进一步，由于(x,y)是式(1)的解，有:

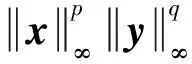
定理2证毕.

2.2 解的下界

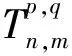
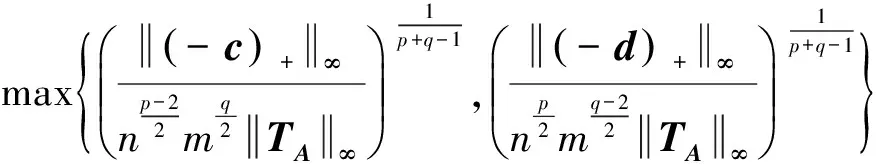
(7)

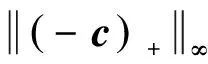
进一步，由TA的定义和定理1，知:

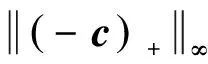
由此，得:

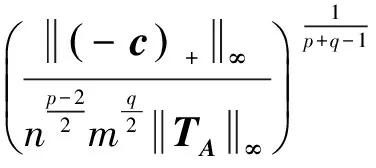
(8)

类似地，可得:

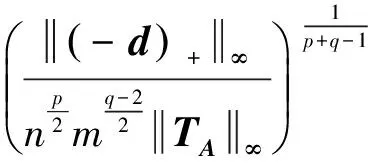
(9)

结合式(8)和式(9)，证得式(7).定理3证毕.

由定理1的2和定理3，可证得如下推论.

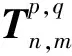
3 结束语

本文利用严格半正张量的相关算子和β(A)，得到了严格半正长方形张量互补问题解的上下界.当m=n且x=y时，本文所考虑问题即为方形张量互补问题，此时所得结论退化为文献[8]中已有的结果.

[1]COTTLERW,PANGJS,STONERE.Thelinearcomplementarityproblem[M].Boston:AcademicPress, 2009:1-37.

[2]HUANGZH,QIL.Formulatingann-personnoncooperativegameasatensorcomplementarityproblem[J].ComputationalOptimizationandApplications, 2016:1-20.

[3]SONGY,QIL.Propertiesoftensorcomplementarityproblemandsomeclassesofstructuredtensors[L/OL].[2016-06-14].http://arxiv.org/abs/1412.0113.

[4]CHEM,QIL,WEIY.Positive-DefiniteTensorstoNonlinearComplementarityProblems[J].JournalofOptimizationTheoryandApplications, 2016,168(2):475-487.

[5]LUOZ,QIL,XIUN.TheSparsestSolutionstoMYMZMYM-TensorComplementarityProblems[L/OL]. [2016-06-14].http://arxiv.org/abs/1505.00993.

[6]DINGW,LUOZ,QIL.P-Tensors,PMYM_0MYM-Tensors,andTensorComplementarityProblem[L/OL]. [2016-06-14].http://arxiv.org/abs/1507.06731.

[7]CHANGK,QIL,ZHOUG.Singularvaluesofarealrectangulartensor[J].JournalofMathematicalAnalysisandApplications, 2010,370(1):284-294.

[8]SONGY,QIL.Onstrictlysemi-positivetensors[L/OL].[2016-07-07].http://arxiv.org/abs/1509.01327.

Estimation of Solutions for Complementarity Problem with Strictly Semi-positive Rectangular Tensor

YU Wen, LING Chen

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

For rectangular tensors, define a continuous positively homogeneous operator and a constant, and prove that the considered rectangular tensor is strictly semi-positive if and only if this constant is positive. On this basis, present some upper and lower bounds of solutions for the complementarity problem with strictly semi-positive rectangular tensor.

tensor; rectangular tensor; strictly semi-positive tensor; tensor complementarity problem; estimation of solutions

10.13954/j.cnki.hdu.2017.02.016

2016-06-20

国家自然科学基金资助项目(11571087)；浙江省自然科学基金重点资助项目(LZ14A010003)

于雯 (1990-),女,辽宁葫芦岛人,硕士研究生，非线性优化.通信作者：凌晨教授，E-mail：macling@hdu.edu.cn.

O221.2

A

1001-9146(2017)02-0077-04