一种用于模拟车辆冲击试验的铁路货车纵向连接模型

杨亮亮，罗世辉，傅茂海，马卫华，冯　征

(1.西南交通大学 牵引动力国家重点实验室，四川 成都　610031；2.西南交通大学 机械工程学院，四川 成都　610031；3.中车南京浦镇车辆有限公司 技术中心，江苏 南京　210031；4.中车青岛四方机车车辆股份有限公司 技术中心，山东 青岛　266111)

大轴重化、长编组化是重载铁路的发展趋势。但随着货车轴重的提高和列车编组数量的增加，势必会加剧车辆之间以及车辆各零部件之间的冲击振动。尽管大冲击行为在车辆服役期间的发生频率并非最高，但却是导致车辆结构及其零部件损坏的主要原因之一，尤其是调车作业时的纵向冲动，一直以来都是车辆运行环境下最恶劣的工况[1]。因此，很有必要通过车辆冲击试验的方法对车辆受关注部位的力、应力、位移、速度、加速度等动态参数进行测量，从而检验车辆及其零部件在大冲击过程中的极限承受能力。

国内外对铁路货车冲击试验的研究主要分为现场试验和数值模拟。前者的试验条件几乎就是驼峰编组作业环境的再现，其分析结果具有极高的真实性，有利于得到正确的结论；后者是利用理论推导、数值积分以及试验修正的方法建立简化的数学模型进行计算机模拟仿真，其分析结果的准确性主要取决于仿真模型的合理性以及现场试验和运用的不断反馈。出于冲击试验成本的考虑，国内外学者更热衷于针对车辆冲击仿真模型进行研究。基于车辆冲击的铁路货车纵向连接模型，通常采用单自由度多质点串联系统来模拟车辆之间的碰撞过程。其中，对缓冲器力学特性多采用查表法[2]、线性阻尼带宽法[3]、迟滞回路修正法[4]、线性与非线性刚度叠加法[5]、多参数刚度阻尼法[6-8]以及斜楔—弹簧推导法[9]等进行数学表达；对于车体结构变形的影响则多采用在缓冲器力学模型中进行补偿，如过渡曲线延伸法[10]、并联刚度阶段作用法[11]等；对于车体与转向架之间的动作用力一般不予关注，即将整个车辆仅视为1个质量块。通过上述仿真分析能够获得车钩力、缓冲器行程、车体速度及加速度等动态参数，并具有较好的预测性。

但由铁路货车运用实践可知，除钩缓装置的结构破坏外，牵引梁的下垂和涨鼓、罐体的挤压、心盘立棱的凹坑和裂纹等也是由大纵向冲击引起的典型破坏现象[12]，而传统连接模型对这些问题并不能较好地进行预测。因此，本文基于车辆及其零部件的纵向力传递细节，提出一种新的货车纵向连接模型。在钩缓组成子模型中考虑缓冲器各摩擦部件之间的几何和力学关系；在心盘组成子模型中考虑上、下心盘之间的黏着、滑动和碰撞行为；此外，还通过在车体结构虚拟体之间加入虚拟弹簧以模拟车体自身的结构变形，使缓冲器的做功环境更接近实际情况。

1　铁路货车纵向连接模型

1.1　纵向冲击微分方程

为了兼顾计算需要与成本，模型中将各车辆的车体和转向架均简化为沿纵向振动的质点系。每个车体由2个串联的分段质量块通过与车体底架结构刚度等效的虚拟弹簧系统进行连接，相邻车体之间由钩缓组成中的弹簧—摩擦系统进行连接，车体与转向架之间由心盘组成中的弹簧—摩擦系统进行连接，从而构成了由有限个质点串并联下的刚度—阻尼振动系统。若不考虑系统外力，编组车辆中任意一个车辆的纵向受力状态如图1所示。图中：mci，mbi分别为第i辆车的车体和转向架质量；Fci，Fci-1分别为第i辆车的车体前、后端车钩纵向作用力；Fpfi，Fpri分别为第i辆车的车体与前、后转向架之间的心盘纵向作用力；Fki为第i辆车的车体底架结构虚拟弹簧力。

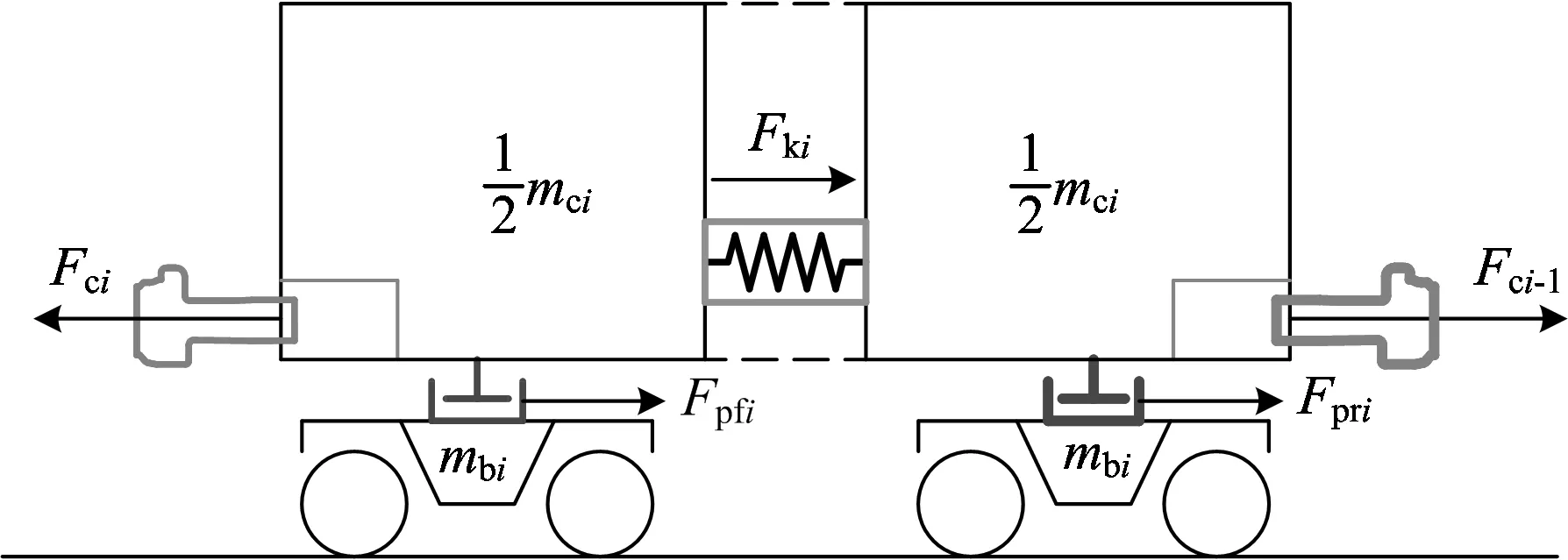
图1　编组车辆中第i辆车的受力示意图

对于编组车辆总数为N的车辆冲击系统而言，其纵向冲击微分方程可描述为

(1)

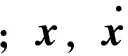
由式(1)可知，该纵向冲击微分方程不仅可以研究各车辆之间的纵向振动问题，还可以研究车体与转向架之间的纵向振动以及车体结构的纵向变形等问题，从而拓展了列车纵向动力学研究的应用领域。

1.2　钩缓组成子模型

以大秦铁路重载货车常用的由17型车钩和MT-2型缓冲器组成的钩缓系统为例，其弹簧阻尼力主要由缓冲器内部的摩擦楔块部件、减振弹簧部件以及复原弹簧部件提供。根据MT-2型弹簧摩擦缓冲器的结构特点及其各零部件的几何装配关系，可将缓冲器的工作过程简化为4个阶段进行分析，即加载Ⅰ阶段、加载Ⅱ阶段、卸载Ⅰ阶段和卸载Ⅱ阶段，其工作原理如图2所示。

1—从板；2—中心楔块；3—楔块；4—动板；5—复原弹簧；6—中心弹簧座；7—外弹簧； 8—内弹簧；9—固定斜板；10—外固定板；11—铜条；12—箱体

由图2可知：在加载Ⅰ阶段中，从板连同中心楔块一起受压运动，但还未触及动板，此时缓冲器能量的耗散主要由楔块分别与中心楔块、固定斜板、中心弹簧座之间的摩擦作用提供；在加载Ⅱ阶段中，随着从板继续压缩至动板处，从板、中心楔块和动板将一起运动，最长可保持到最大压缩状态，此时缓冲器内部的摩擦作用除了上述的楔块摩擦外，还包括动板与固定外板和固定斜板之间的相对摩擦；卸载过程中缓冲器的作用机理与加载过程类似，只是各弹簧及摩擦部件相对加载阶段的运动方向相反。

若假设缓冲器内部各摩擦面的相对运动始终处于缓慢、稳定的滑动摩擦状态，则可通过力的平衡条件对缓冲器的中心楔块、楔块、中心弹簧座和动板进行准静态分析。根据缓冲器在4个阶段的几何位置和受力状态特点，经推导可得出缓冲器在准静态下做功的力学特性，如图3所示。

图3　缓冲器准静态示功图

在准静态下，缓冲器的阻抗力Fr主要表现为弹簧力和滑动摩擦力的合力Fsf，其与纵向位移x、弹簧刚度k、摩擦倾角θ及摩擦系数μ参数有关，可以表示为

Fr=Fsf(x,k,θ,μ)

(2)

上述表达式是基于缓冲器处于准静态的理想情况，其力学特性中的加载、卸载及过渡曲线仅描述了主弹簧、复位弹簧的弹力以及各摩擦面的动摩擦力随位移的变化情况，并未考虑各摩擦面运动状态的改变。实际调车或列车工况中，缓冲器在加载结束阶段和卸载开始阶段均会出现尖峰效应[13-14]，这是由于该阶段下的各摩擦面相对滑动速度较低，即摩擦运动处于弱锁定状态，且锁定后的摩擦系数明显大于滑动时的摩擦系数，从而引起了缓冲器阻抗力的局部突变。为了较准确地描述相对速度对摩擦阻力的影响，引入附加摩擦系数表示动态摩擦向静态摩擦转换时的黏滞补偿，以速度为自变量并线性化为

(3)

式中：μa为附加摩擦系数；μs为等效静态摩擦系数；μk为等效动态摩擦系数；Δv为摩擦相对速度；ver为动、静摩擦之间转换速度的阈值。

在动态下，缓冲器的阻抗力Fr相当于缓冲器的弹簧力、滑动摩擦力的合力Fsf以及摩擦锁定后的附加摩擦力Faf的总和，即

Fr=Fsf(x,k,θ,μ)+Faf(x,v)

(4)

通过计算可以得到典型弹簧摩擦缓冲器的动态阻抗特性，如图4所示。由图4可知，加载曲线末端和卸载曲线始端均出现了不同程度的尖峰效应，前者会引起车钩力的陡然增大，产生瞬间的刚性冲击，后者则易引起弹簧回复力不足，导致缓冲器卡死。

图4　缓冲器动态示功图

于是，单个缓冲器的力学特性可以描述为

Fr(xt,vt)=

(5)

式中：xt和xt-Δt分别为当前时间t和上一个时间t-Δt(Δt为时间步长)缓冲器的位移；vt和vt-Δt分别为对应的缓冲器速度；Fr(xt,vt)和Fr(xt-Δt,vt-Δt)分别为对应的缓冲器阻抗力；FLsf和FUsf分别为弹簧和滑动摩擦引起的加、 卸载力；FLaf和FUaf分别为附加摩擦引起的加、 卸载力；kr为过渡刚度函数。

若将钩缓组成简化为1对连挂车钩和2个缓冲器的串联体，随着车端相对位移的正负变化，车钩表现为拉伸与压缩的转换，但缓冲器始终都是处于受压缩的状态。由于钩缓组成的质量远小于车体的，可视2个缓冲器的受力过程完全一致，从而可将车钩力和缓冲器阻抗力的关系表示为

(6)

式中：Fc为车钩力；Δxc为钩缓组成端部串联的2个刚体之间相对位移。

1.3　心盘组成子模型

考虑车体上心盘与转向架下心盘之间的纵向力传递过程，可将两者之间的纵向连接关系简化为1个两自由度体的摩擦碰撞振动系统[15-16]，如图5所示。图中：Fpin为中心销接触力；Ffri为心盘切向摩擦力；Frim为边缘接触力。

图5　车体与转向架之间纵向受力示意图

1次完整的摩擦碰撞过程存在3种运动状态，即黏着、滑动和碰撞，当上、下心盘的相对位移小于装配间隙且相对速度小于黏滑摩擦转换速度时，心盘组成处于黏着状态；当上、下心盘的相对速度大于黏滑摩擦转换速度时，心盘组成处于滑动状态；当上、下心盘的相对位移大于装配间隙时，心盘组成处于碰撞状态。因此，车体与转向架之间的纵向作用力为上、下心盘间的纵向黏滑摩擦力和纵向接触力的总和。

黏滑摩擦状态下，车体上心盘面与转向架下心盘面之间的均向摩擦力可以表示为

Ffri(Δxp,Δvp)=

(7)

式中：Fn为心盘垂向接触力；Δxp和Δvp分别为车体上心盘与转向架下心盘之间的纵向相对位移和速度；vep为黏滑摩擦转换速度；k0和c0分别为黏滑摩擦状态下的等效刚度和阻尼，一般与材料的特性和表面状态有关；μp为滑动摩擦系数。

车体上心盘边缘与转向架下心盘立棱之间的接触力可以表示为

Fcon(Δxp)=

(8)

式中：Fcon为心盘纵向接触力；r1为上心盘边缘与下心盘立棱之间的间隙；r2为上心盘中心孔与中心销之间的间隙；kp1为心盘衬垫的压缩刚度；kp2为摇枕的弯曲刚度。

需要指出的是，车体和摇枕之间的点头运动关系对心盘纵向力的影响较小，这是由于纵向冲动下车体与转向架连接处的最大冲击力主要来源于接触力，而非摩擦力，因此可忽略由心盘垂向载荷的变化而引起的动摩擦力改变量，即视心盘平面为1个仅考虑纵向载荷变化的集中力元。于是，心盘组成的刚度阻尼系统可简化为车体与转向架纵向伸缩的弹簧和摩擦运动，心盘纵向力Fp可以描述为

(9)

式中：fp为心盘组成的非线性黏滑—碰撞函数。

1.4　车体结构子模型

车体在承受纵向拉伸或压缩作用时会发生结构变形，在车体额定承载范围内，变形量与作用力大小基本呈比例关系，即车体的纵向刚度可近似为线性。需要指出的是，车体刚度并非只在缓冲器处于全压缩状态时才起作用，而是始终与缓冲器刚度串联并共同缓和纵向冲击力，尤其是当车体刚度接近某个时刻的缓冲器刚度时，其结构缓冲效应的影响将更显著。

车体刚度受车体结构参数的影响非常大，由于货车车体底架结构模式的多样化、纵向载荷传递路径的差异、结构中材料属性的不统一等，使得车体的纵向刚度也存在差别。因此，本文采用有限元方法获取不同车体结构的纵向位移随纵向力的变化规律[17]。其中，拉伸为正，约束和载荷的参考点为前从板座；压缩为负，约束和载荷的参考点为后从板座。

从纵向力在车体底架中的承载模式角度，可分为中边梁承载式、中梁承载式以及边梁承载式3种底架结构模式，如图6所示。

图6　纵向力作用下的车体底架承载模式

分别以采用这3种车体底架承载模式的敞车为例，得到不同车体底架承载模式下从板座处产生的纵向位移随纵向力的变化曲线，如图7所示。由图7可知：由于型材截面的几何尺寸和厚度不同，一般中梁承载式底架的车体拉压和弯曲刚度要比边梁大，中、边梁共同承载式底架的车体纵向刚度最大，中梁承载式底架的车体次之，边梁承载式底架的车体最小。

图7不同车体底架承载模式下从板座处产生的纵向位移随纵向力的变化

由纵向力引起的车体变形，可以分为拉压型和弯曲型2种类型，如图8所示。

一般而言，中部呈凹或凸型的车体结构在纵向力作用下将产生附加偏心弯曲变形，从而引起更大的纵向累积变形。因此，图8中无底架罐车的车体纵向刚度比有底架罐车低，如图9所示。

需要指出的是，由上述有限元方法得到的车体纵向刚度是车体结构在伸缩和弯曲方向的单位纵向力变形总和。此外由图9可知，在车体额定承载范围内，从板座处产生的纵向位移与施加的纵向力基本呈线性关系。因此，复杂的车体结构刚度可通过在前、后2个车体结构虚拟体间加入虚拟弹簧进行模拟，即假设整个车体结构的纵向累积变形都集中到虚拟弹簧处发挥作用，如图10所示。该虚拟弹簧力相当于车体结构的纵向作用力，可描述为

图8　纵向力作用下的车体变形类型

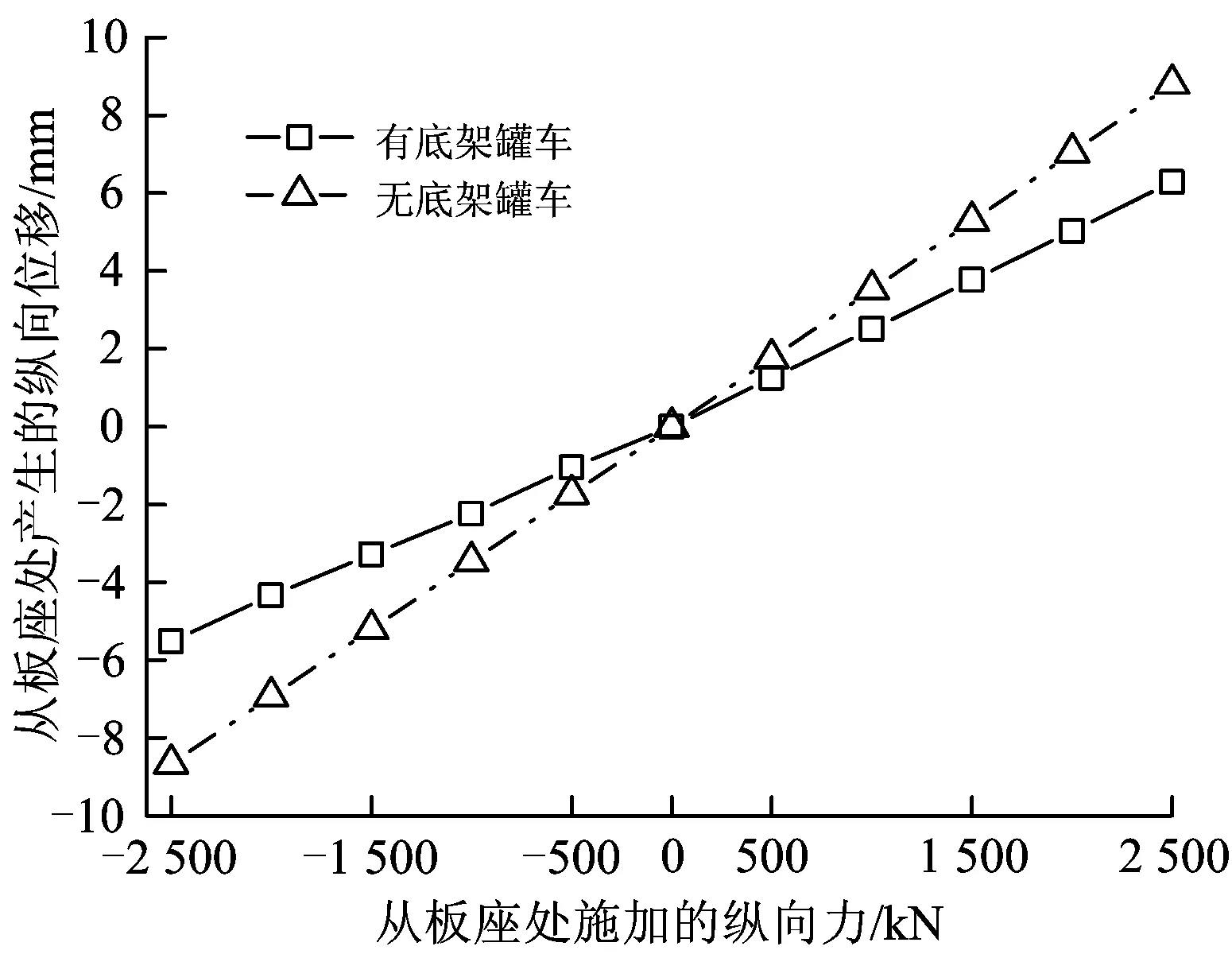
图9不同车体变形类型下从板座处产生的纵向位移随纵向力的变化

Fk=fk(Δxk)

(10)

式中：fk为车体底架结构的虚拟弹簧等效刚度函数，一般而言，拉伸刚度要略小于压缩刚度；Δxk为前、后2个车体结构虚拟体之间的相对位移。

图10　考虑结构变形的车体纵向连接示意图

2　仿真结果的输出和验证

根据车辆冲击微分方程及车辆纵向连接函数表达式，采用MATLAB软件编制了用于车辆冲击仿真试验的纵向动力学计算程序。以C80型运煤专用敞车为例，设冲击速度为8 km·h-1，冲击重量均为100 t，车钩间隙为9.5 mm，上、下心盘径向间隙为2.5 mm，经仿真计算可以获得车辆纵向冲击响应，即各刚体在冲撞瞬间力、速度和位移等的变化情况，如图11—图14所示。

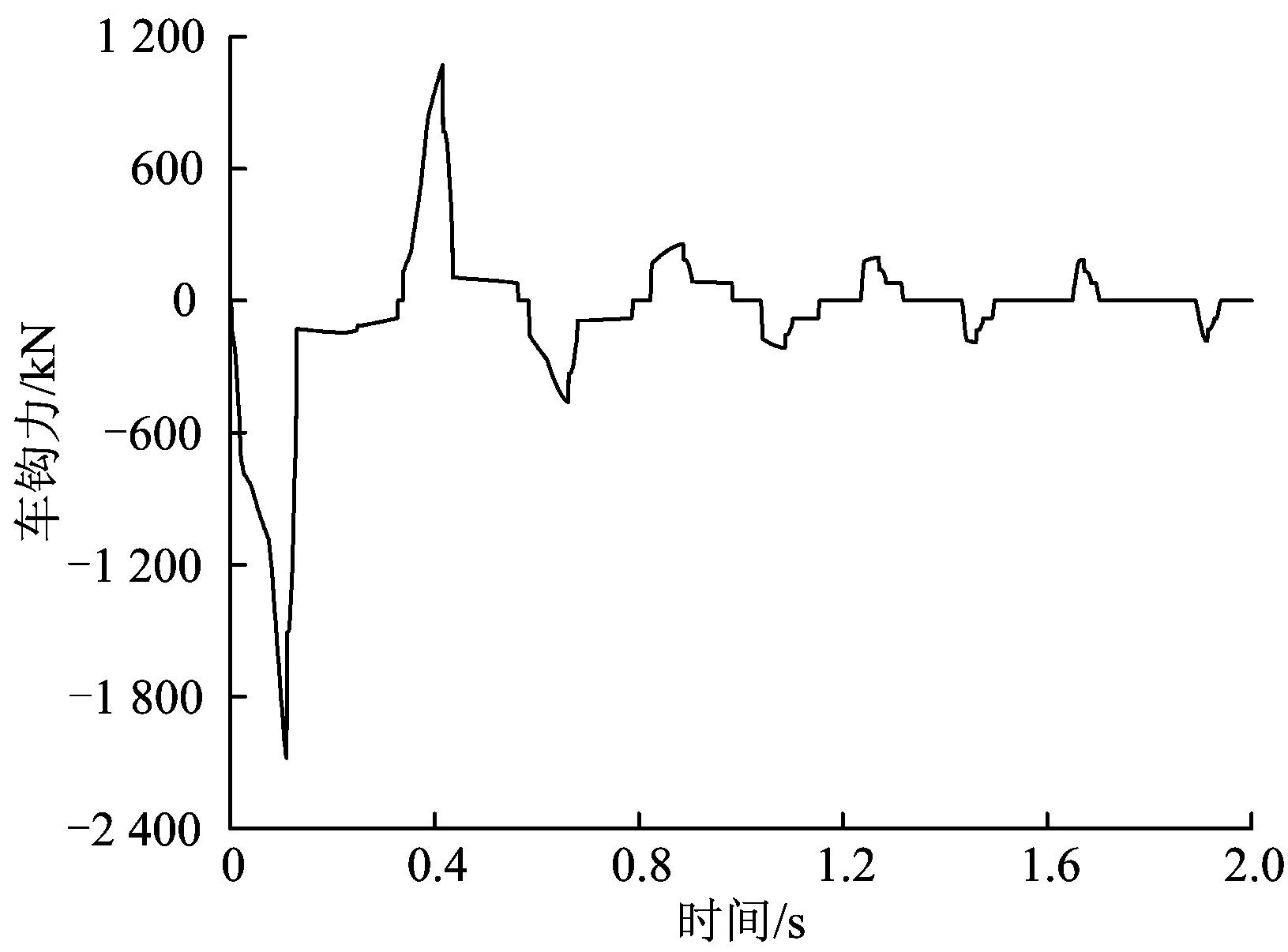
图11　车钩力随时间变化

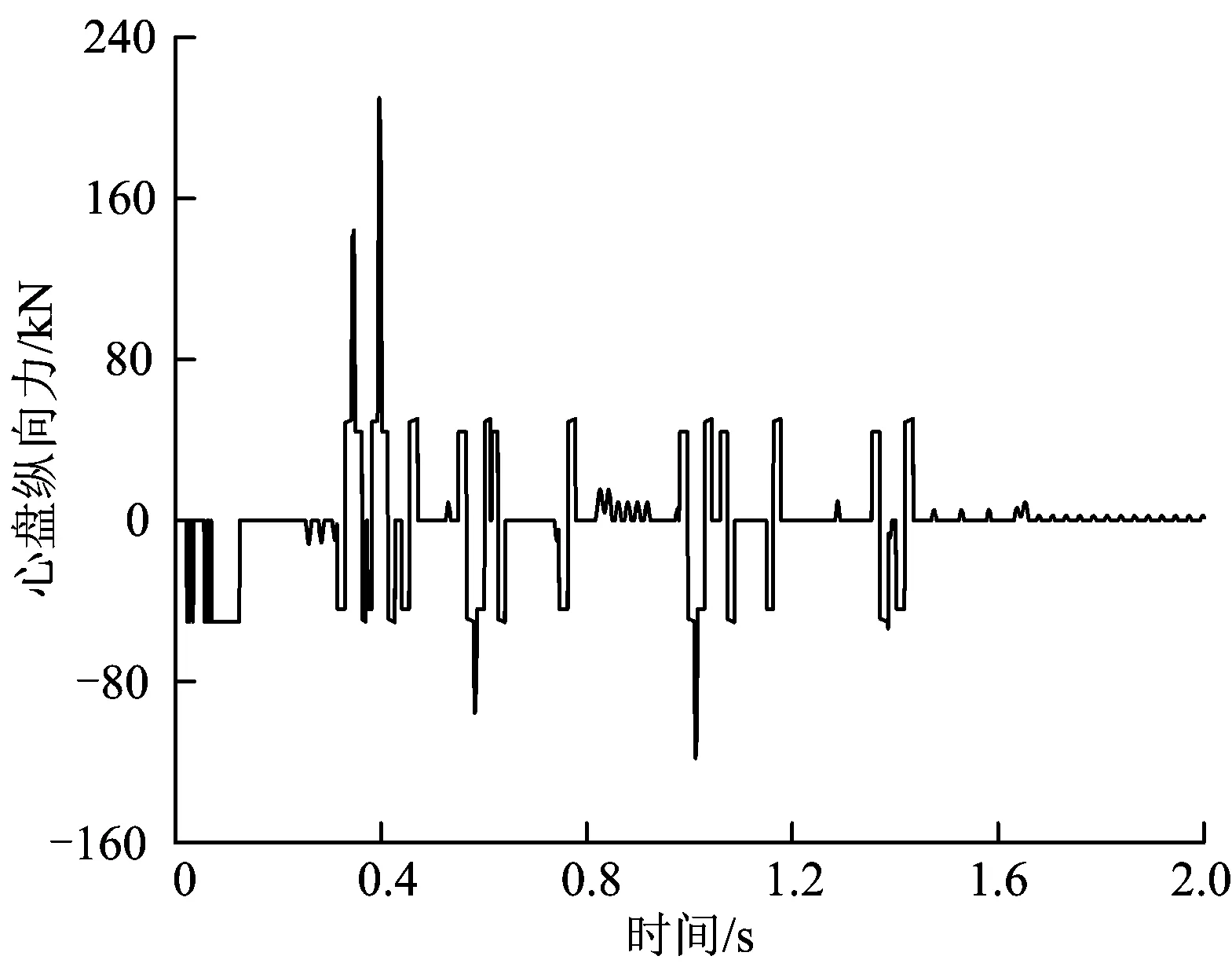
图12　心盘纵向力随时间的变化

由图11和图12可知：计算结果很好地反映了调车冲击过程中缓冲器的阻抗特性、心盘组成的摩擦—碰撞特性；其中，车钩力随时间变化的波形具有一定的规律性，各极值均未超出MT-2型缓冲器的允许范围，最大车钩力出现在第1个振动半周期内，并在2个振动周期后衰减至10%以下；而心盘纵向力随时间变化的波形则呈现脉冲波形，与车钩力不同，其最大值并未出现在车辆撞击后的第1个振动半周期内，而是出现在第2个振动半周期内，此时车钩处于拉伸状态，且车体与转向架的运动方向相反。

图13　车体、转向架速度随时间的变化

由图13可知：由于车体与转向架的质量不等，导致了碰撞后各自振动特性的差异，转向架速度的变化波形相当于是在车体速度交替变化的基础上叠加了由转向架惯性冲击引起的速度变化。

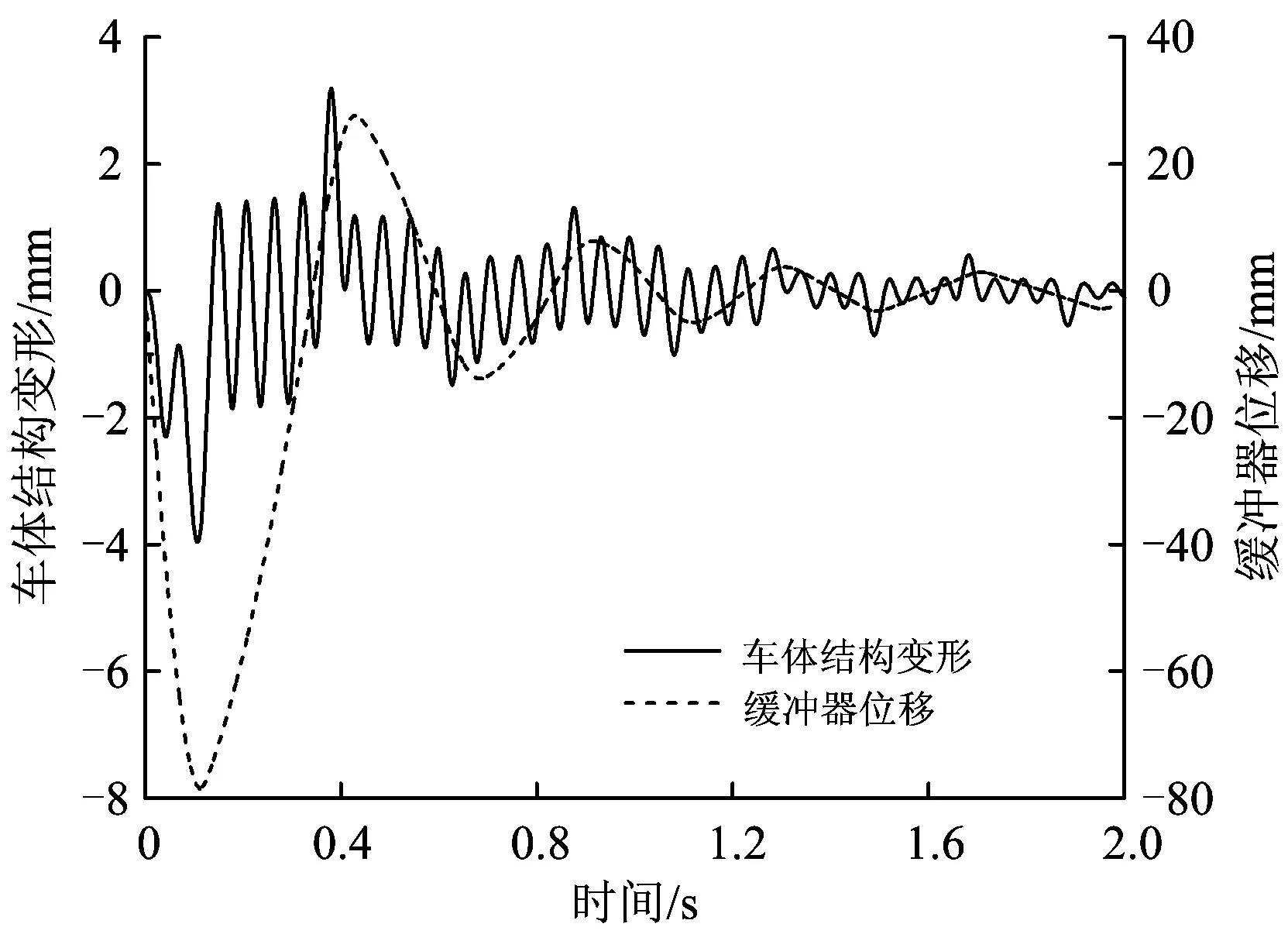
图14　缓冲器位移和车体结构变形随时间的变化

由图14可知：车辆在调车冲击过程中，车体结构的最大变形量约为4 mm，尽管仅相当于缓冲器最大位移量的5%左右，但该微小变形仍一定程度地延长了力作用时间，起到了缓和纵向冲击的效果。

为了比较仿真和试验下的车辆冲击结果，两者采用相同的冲击条件和采样频率，且测试点均取在被冲击车的冲击端处。其中，现场冲击试验细节主要参考标准TB/T 2369—2010《铁道车辆冲击试验方法》，车钩、摇枕载荷采用贴电阻应变片法进行测量，缓冲器行程采用贴差动式位移传感器法进行测量，冲击速度采用轨道贴片法进行测量；冲击和被冲击货车的冲击质量均为100 t；采样频率为100 Hz。对比结果如图15和图16所示。

图15　仿真和试验下的缓冲器示功图

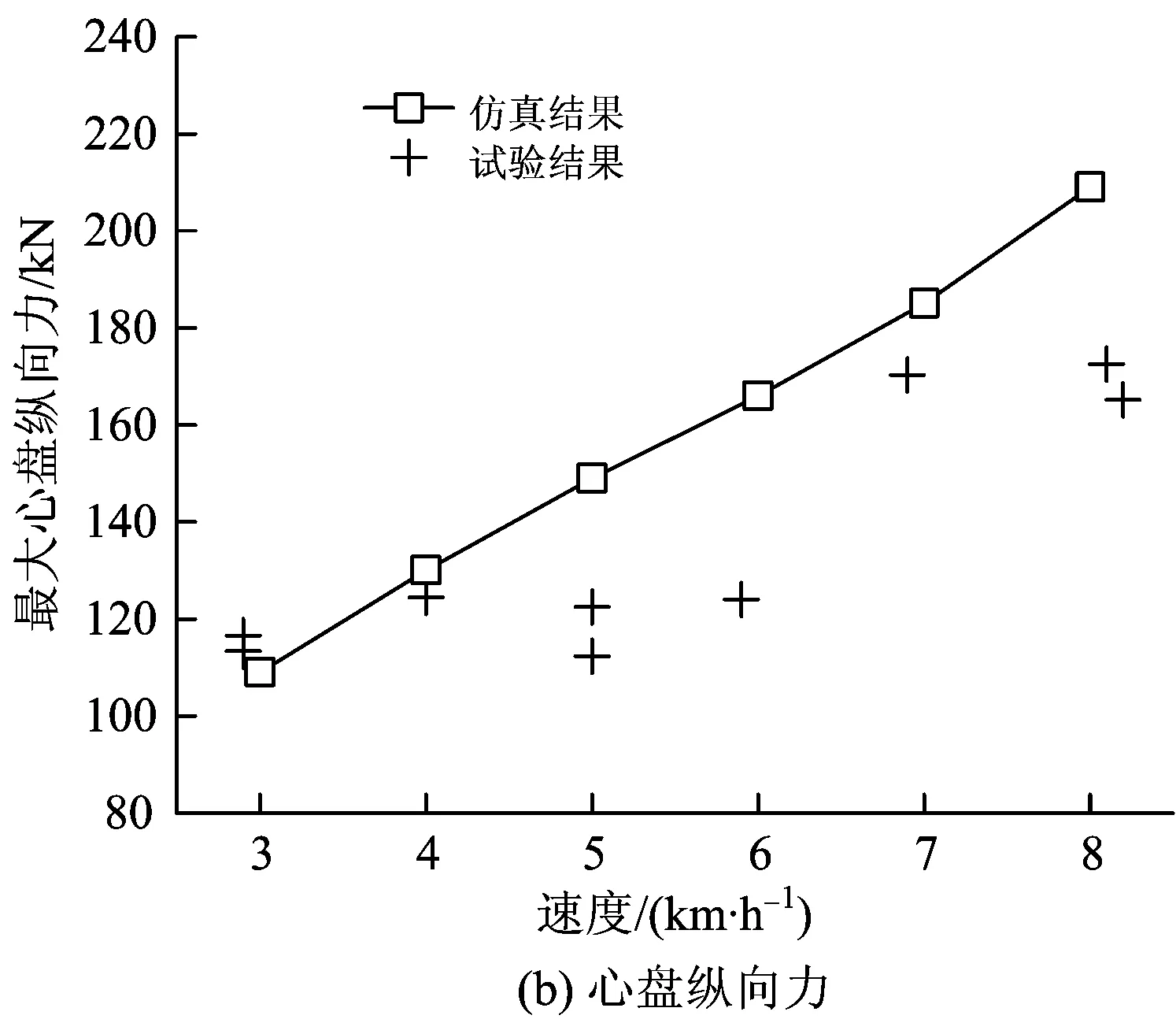
图16　仿真和试验下最大的车钩力和心盘纵向力

由图15和图16对比可知：仿真和试验下的缓冲器示功图基本吻合，较好地体现了缓冲器在受冲击作用下的加、卸载过程；缓冲器最大位移、阻抗力及做功量的仿真值与其试验值虽具有一定的偏差，但相对误差均在10%以内；对于仿真结果和试验结果存在一些差异，尤其是在加载Ⅰ阶段与加载Ⅱ阶段之间的过渡处，试验结果的间断突变现象并不像仿真结果那样明显，这可能与仿真时忽略各摩擦部件质量有关；因此，该缓冲器的力学模型还有待进一步完善，应结合缓冲器内部各摩擦面的工作状态，如表面粗糙度、温度、湿度等参数影响规律综合考虑。此外，仿真和试验下最大车钩力和心盘纵向力随速度的变化趋势基本一致，其中，车钩力的差异性较小，摇枕横向载荷(心盘纵向力)的差异性较大，这主要是受仿真模型的简化以及试验条件不确定性的影响，包括货物内部耗散、车辆悬挂系统、测试仪器和天气状况等。因此，提高仿真模型的模拟精度、采集更多试验样本是缩小车辆冲击仿真与试验结果的有效途径；需要指出的是，调车冲击是典型的瞬态过程，属于非线性冲击力学的研究范畴，但仅从工程应用的角度考虑，上述仿真结果的误差是可以接受的。

3　结　论

(1)基于车辆及其零部件的纵向力传递细节，提出了一种用于模拟车辆冲击试验的铁路货车纵向连接模型。其中，车端连接子模型考虑了缓冲器各摩擦部件之间的几何和力学关系；车体与转向架连接子模型考虑了上、下心盘之间的黏着、滑动和碰撞行为；此外，还通过在车体离散体之间加入虚拟弹簧模拟车体自身的结构变形影响。

(2)提出的铁路货车纵向连接模型更符合车辆的实际运用状态，且车辆冲击试验的仿真结果也非常贴近现场试验结果。利用该模型不仅可以研究各车辆之间的纵向振动问题，还可以研究车体与转向架之间的纵向振动以及车体结构纵向变形等问题，从而拓展了列车纵向动力学研究的应用领域。

(3)提出的铁路货车纵向连接模型仅是基于一维列车的纵向振动系统，各连接子模型的模拟方法具有一定的局限性，仿真输出结果也存在一些偏差，但对车辆冲击试验的前期预测提供了有价值的理论参考。

[1]严隽耄,傅茂海.车辆工程[M].北京:中国铁道出版社, 2008.

[2]GOGINENI B R, GARG V K. A Dynamic Model for Longitudinal Train Action [R]. Washington DC: The Association of American Railroads, 1978.

[3]XU Z Q, MA W H, WU Q, et al. Analysis of Coupler Rotation Angle in Heavy Haul Locomotives [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2014, 228(8): 835-844.

[4]常崇义,王成国,马大炜,等. 2万t组合列车纵向力计算研究[J].铁道学报, 2006, 28(2): 89-94.

(CHANG Chongyi, WANG Chengguo, MA Dawei, et al. Study on Numerical Analysis of Longitudinal Forces of the T20 000 Heavy Haul [J]. Journal of the China Railway Society, 2006, 28(2): 89-94. in Chinese)

[5]金星,罗运康.摩擦型缓冲器特性的数学描述[J].铁道车辆, 2011, 49(6): 1-4.

(JIN Xing, LUO Yunkang. The Mathematic Description of Features of the Friction Type Draft Gears [J]. Rolling Stock, 2011, 49(6): 1-4. in Chinese)

[6]WARD E D, LEONARD R G. Automatic Parameter Identification Applied to a Railroad Car Dynamic Draft Gear Model [J]. Transactions of the ASME, 1974: 460-465.

[7]ГРЕБЕНЮК П Т. 超重列车制动动力学[M]. 陈方昌,樊连波,译. 北京:中国铁道出版社, 1984.

[8]魏伟,赵连刚.两万吨列车纵向动力学性能预测[J].大连交通大学学报, 2009, 30(2): 39-43.

(WEI Wei, ZHAO Liangang. Prediction of Longitudinal Dynamic Coupler Force of 20 000 Ton Connected Train [J]. Journal of Dalian Jiaotong University, 2009, 30(2): 39-43. in Chinese)

[9]COLE C. Longitudinal Train Dynamics: Characteristics, Modelling, Simulation and Neural Network Prediction for Central Queensland Coal Trains [D]. Rockhampon：Central Queensland University, 1999.

[10]黄运华,李芾,傅茂海.车辆缓冲器特性研究[J].中国铁道科学, 2005, 26(1): 95-99.

(HUANG Yunhua, LI Fu, FU Maohai. Research on the Characteristics of Vehicle Buffers [J]. China Railway Science, 2005, 26(1): 95-99. in Chinese)

[11]ANSARI M, ESMAILZADEH E, YOUNESIAN D. Longitudinal Dynamics of Freight Trains [J]. International Journal of Heavy Vehicle Systems, 2009, 16(1/2):102-131.

[12]铁道部运输局装备部.铁路货车典型故障汇编[M].北京:中国铁道出版社, 2008.

[13]COLE C, SUN Y Q. Simulated Comparisons of Wagon Coupler Systems in Heavy Haul Trains [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit， 2006,220(6):535-546.

[14]WU Q, SPIRYAGIN M, COLE C. Advanced Dynamic Modelling for Friction Draft Gears [J]. Vehicle System Dynamics， 2015,53(4):475-492.

[15]SIMSON S A, PEARCE M. Longitudinal Impact Forces at 3 Piece Bogie Center Bearings [C]//Proceedings of the 2005 ASME/IEEE Joint Rail Conference: Research and Testing for Industry Advancement. Pueblo: American Society of Mechanical Engineers,2005:45-50.

[16]杨亮亮,罗世辉,傅茂海,等.三大件转向架摇枕纵向载荷的数值模拟研究[J]. 中国铁道科学, 2014, 35(5): 62-69.

(YANG Liangliang, LUO Shihui, FU Maohai, et al. Numerical Simulation of Longitudinal Load on Bolster of Three-Piece Bogie [J]. China Railway Science, 2014, 35(5): 62-69. in Chinese)

[17]杨亮亮,罗世辉,傅茂海,等. 基于纵向冲动的混编货物列车编组方案研究[J]. 中国铁道科学, 2015, 36(4): 108-114.

(YANG Liangliang, LUO Shihui, FU Maohai, et al. Marshalling Scheme of Mixed Formation Freight Train Based on Longitudinal Impulse [J]. China Railway Science, 2015, 36(4): 108-114. in Chinese)