基于改进的PESP模型编制高速铁路周期性列车运行图的研究

李得伟，丁世顺

(北京交通大学 轨道交通控制与安全国家重点实验室，北京　100044)

列车运行图是高速铁路行车组织的基础，其编制质量直接影响行车的安全和效率。周期性列车运行图是指在每个周期时段内，列车运行线都具有相同的模式[1]。与非周期列车运行图相比，周期性列车运行图具有便于旅客记忆、行车组织有规律、有利于合理组织列车衔接等优点。因此，国外高速铁路发达国家如日本、法国、德国等均广泛采用周期性列车运行图。

国外学者对周期性列车运行图的编制问题进行了大量的研究。Serafini等[2]首次提出了周期事件规划问题(Periodic Event Scheduling Problem，PESP)模型，并将PESP模型应用在机车调度等计划的编制中。Voorhoeve[3]首先采用PESP模型解决荷兰铁路周期性列车运行图的编制问题。Lindner[4]综合研究了列车开行方案和列车运行图编制的问题，开发了求解PESP模型的分支定界算法。Peeters[5]在PESP模型的基础上提出CPF(Cycle Periodicity Formulation)模型，通过在CPF模型中加入车站通过能力约束，从而提高了周期性列车运行图的编制质量。

国内也有学者对编制适合我国铁路运营特点的周期性列车运行图问题进行了研究。汪波等[6]在PESP模型的基础上利用约束图建立了周期势差模型，并应用周期势差模型编制了京津城际高速铁路不同列车开行方案下的周期性列车运行图。谢美全等[7]提出定序的周期性列车运行图编制模型，该模型考虑了列车对到发时刻的特殊要求，使得编制的列车运行图的适应性更高。聂磊等[8]研究了计算机编制周期性列车运行图的关键技术，为计算机自动编制周期性列车运行图提供了技术支撑。

既有研究为解决我国铁路周期性列车运行图的编制问题奠定了基础，而且基于PESP模型编制周期性列车运行图已经成为业界共识。由于我国铁路的列车数量多、运行线路长、停站多而复杂，国外的研究成果无法直接应用到我国铁路；而我国的既有研究大多针对的是较简单的小规模场景。对于求解大规模周期性列车运行图模型时无解的问题，国内外的研究还不多。作者通过研究发现，当求解问题规模较大时导致无解的主要原因是PESP传统模型中的固定列车区间运行时间约束较为严格。基于这一发现，本文在PESP传统模型[5]的基础上，提出1种改进的PESP模型，用于编制适合我国高速铁路的周期性列车运行图。

1　PESP改进模型

1.1　目标函数

为了最大化企业利益，提高动车组的运用效率，在用于编制高速铁路周期性列车运行图的PESP改进模型中以列车的总运行时间t总最小为目标函数，可以表示为

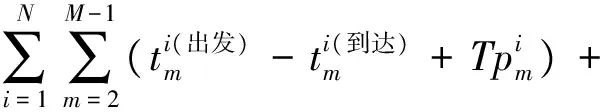
(1)

1.2　约束条件

1)可变区间运行时间约束

在PESP传统模型中列车的区间运行时间约束是严格的等式约束，如式(2)所示，由于解空间受限，求解大规模问题时易出现无解的情况。为了解决这一问题，本文提出可变的区间运行时间约束，即允许列车的区间运行时间在一定范围内变动，改进的区间运行时间约束如式(3)所示。

i=1，2，…，N；m=2，3，…，M

(2)

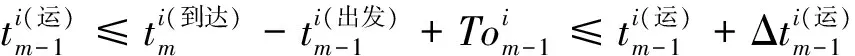
i=1，2，…，N；m=2，3，…，M

(3)

其中，

i=1，2，…，N；m=2，3，…，M

(4)

2)可变停站时间约束

列车在车站的停站时间约束可以表示为

i=1，2，…，N；m=2，3，…，M-1

(5)

3)列车运行安全间隔时间约束

当列车在区间内的运行时间可变后，由于PESP传统模型的列车运行安全间隔时间约束中包含列车的区间运行时间，因此，原有约束不再适用。为解决这一问题，需要将PESP传统模型的列车运行安全间隔时间约束分解为2个与列车的区间运行时间无关的约束：列车出发安全间隔时间约束和列车到达安全间隔时间约束，如式(6)和式(7)所示。

i和j=1，2，…，N；j>i；m=1，2，…，M-1

(6)

i和j= 1，2，…，N；j>i；m=1，2，…，M-1

(7)

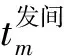
4)同类列车服务均衡性约束

(8)

5)列车到达和出发时间范围约束

根据运输组织的要求，某些列车在车站的出发和到达时间需要固定在特定的时间范围内，可以表示为

(9)

(10)

1.3　模型求解

本文给出的PESP改进模型为单目标线性混合整数规划模型，可以利用数学优化软件如ILOG CPLEX进行求解，但有以下2个关键问题需要解决。

1)模型的求解效率问题

2)模型的一般性问题

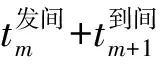
图1　区间运行时间之差大于或等于

2　实例验证

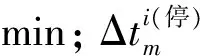
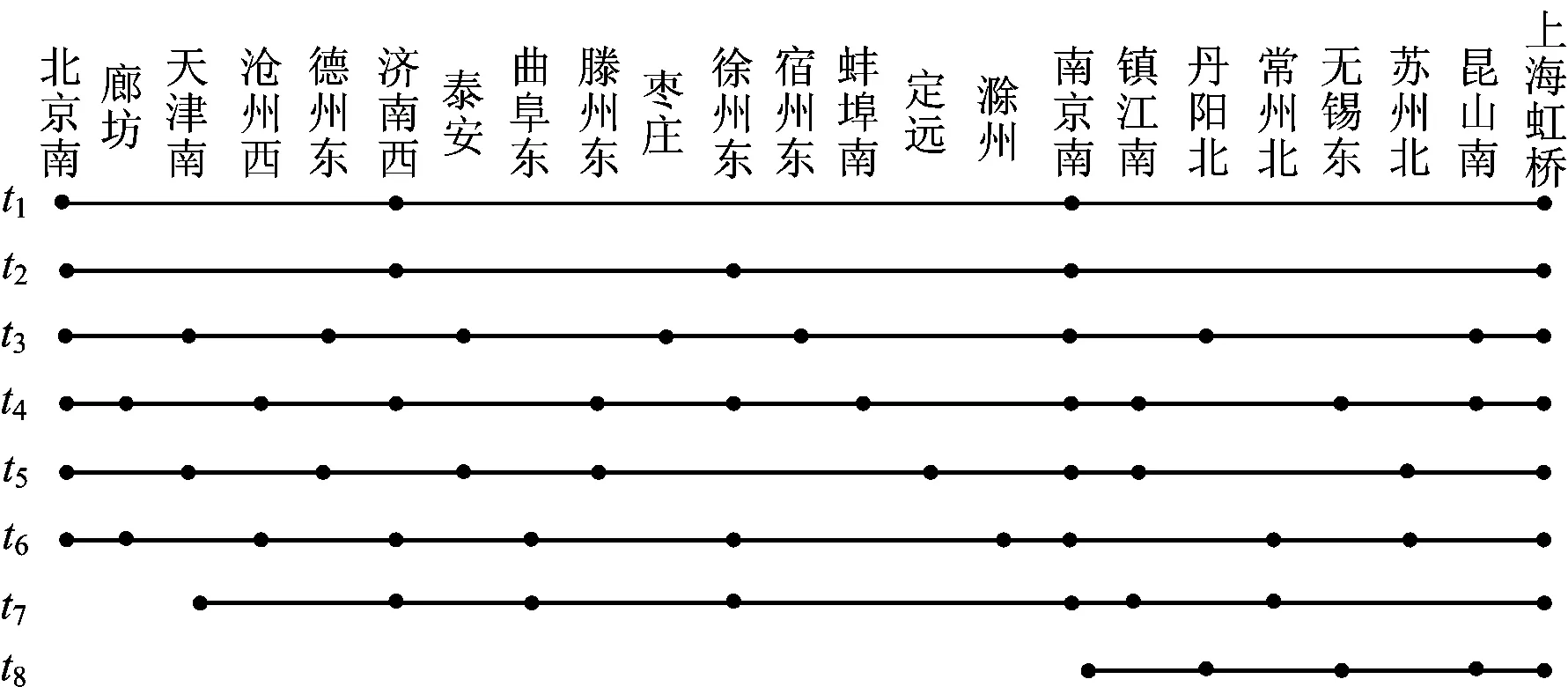
图2　列车开行方案

序号区间纯运行时分/min1北京南—廊坊162廊坊—天津南133天津南—沧州西184沧州西—德州东215德州东—济南西196济南西—泰安137泰安—曲阜东148曲阜东—滕州东119滕州东—枣庄710枣庄—徐州东1311徐州东—宿州东1412宿州东—蚌埠南1813蚌埠南—定远1114定远—滁州1315滁州—南京南1316南京南—镇江南1517镇江南—丹阳北618丹阳北—常州北719常州北—无锡东1220无锡东—苏州北521苏州北—昆山南622昆山南—上海虹桥12

通过求解发现，使用PESP传统模型无法在有限时间内得出最优解；然而使用本文的PESP改进模型，能够快速求得最优目标函数值为2 394 min，求解时间为305 s，求解得到的结果如图3所示，验证了PESP改进模型适用于规模较大的高速铁路周期性列车运行图编制问题。

3　灵敏度分析

图3　京沪高速铁路下行方向的周期性列车运行图

3.1　允许的区间运行时间变化量对求解效果的影响

表的取值对模型求解结果的影响

3.2　允许的停站时间变化量对求解效果的影响

3.3　割平面对模型求解时间的影响

为了在保证求解可行性的同时提高求解效率，本文通过在求解过程中引入割平面以减小搜索空间。固定其他参数，研究加入割平面和不加入割平面时模型的求解时间，结果见表4。由表4可知，在求解过程中引入割平面能够显著缩短模型的求解时间。

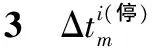
表的取值对模型求解效果的影响

表4　加入割平面前后的模型求解时间对比

4　结　语

本文对编制周期性列车运行图所采用的PESP传统模型进行了改进。在PESP改进模型中以列车的总运行时间最小为目标函数，采用可变的区间运行时间约束，并将列车运行安全间隔时间约束分解为2个与列车的区间运行时间无关的约束，以实现对大规模高速铁路周期性列车运行图编制问题的求解。通过编制京沪高速铁路下行方向的周期性列车运行图验证了PESP改进模型的有效性。分析PESP改进模型中参数的取值对模型求解质量和求解效率的影响，结果表明，随着允许的区间运行时间变化量和停站时间变化量的增大，PESP改进模型的求解时间也随之大幅增加。为此在求解模型时采用了加入割平面的方法，从而使PESP改进模型的求解效率得到大幅度提高。

[1]杨东方. 计算机编制客运专线周期性列车运行图的研究[D].北京：北京交通大学，2009.

(YANG Dongfang. Study on Computer Aided Working out Cyclic Train Timetable for Passenger Dedicated Line[D]. Beijing：Beijing Jiaotong University，2009. in Chinese)

[2]SERAFINI P，UKOVICH W. A Mathematical Model for Periodic Event Scheduling Problems[J]. SIAM Journal on Discrete Mathematics，1989，2(4)：550-581.

[3]VOORHOEVE M. Rail Scheduling with Discrete Sets[R]. Eindhoven：Eindhoven University of Technology，1993.

[4]LINDNER T. Train Schedule Optimization in Public Rail Transport[D]. Braunschweig：Technical University Braunschweig，2000.

[5]PEETERS L. Cyclic Railway Timetable Optimization[D]. Rotterdam：Erasmus University Rotterdam，2003.

[6]汪波，杨浩. 周期运行图编制模型与算法研究[J]. 铁道学报，2007，29(5)：1-6.

(WANG Bo，YANG Hao. Study on Model and Algorithm of Periodic Train Diagram Generation[J]. Journal of the China Railway Society，2007，29 (5)：1-6. in Chinese)

[7]谢美全，聂磊. 周期性列车运行图编制模型研究[J]. 铁道学报，2009，31(4)：7-13.

(XIE Meiquan，NIE Lei. Model of Cyclic Train Timetable[J]. Journal of the China Railway Society，2009，31(4)：7-13. in Chinese)

[8]聂磊，张渊，武鑫. 计算机编制周期性列车运行图关键技术[J]. 中国铁道科学，2014，35(1)：114-121.

(NIE Lei，ZHANG Yuan，WU Xin. Key Technologies for Computer Generation of Cyclic Train Timetable[J]. China Railway Science，2014，35(1)：114-121. in Chinese)