树枝形货物作业点取送车作业方案的多目标优化模型及算法

郭垂江

(湖南铁路科技职业技术学院 运输管理学院，湖南 株洲　412006)

车站是铁路运输生产的基层单位，货场和专用线是铁路车站的货物装卸作业地点，可以统称为货物作业点，按其与车站的位置关系可分为放射形、树枝形和混合形3类。合理安排调车机车(简称为调机)的取送作业顺序，能使调机在最短的时间内完成取送车作业，从而提高调机的使用效率，减少车辆的非作业等待时间。

对于树枝形货物作业点取送车作业方案优化问题的研究，一般做法是将其转换成求解哈密尔顿图最短回路问题，部分学者采用2—交换[1]、最小生成树算法[2]、动态规划方法[3]得到最优解，但计算过程比较复杂；部分学者采用遗传算法[4]等现代智能算法进行计算，得到问题的满意解。树枝形货物作业点取送车作业形式有单一取车、单一送车、送车兼调移车、取车兼调移车、取送车结合、送调取车结合等6种。目前绝大多数研究成果没有把调移作业考虑到取送车作业中，因而所建立的模型难以适应铁路现场复杂的作业组织形式，从而影响模型及算法的实际应用。文献[5—6]认为调移作业是调机访问相应货物作业点必须满足的优先关系，从而将树枝形专用线取送车作业优化问题转换成满足所有优先权关系的哈密尔顿最短回路问题，分别利用改进破圈连接法和启发式算法进行求解，但仅以调机取送车总时间最小为优化目标，这在一定程度上也存在局限性。文献[7]分别以调机取送车总时间、车辆的总入线车辆小时和总走行车辆公里最小为优化目标，较好地反映了树枝形货物作业点取送车作业方案优化问题的实质，但未对如何平衡这3个优化目标及如何将调移作业考虑到模型中做进一步的研究。文献[8]从顺序和批次2个优化维度建立了铁路车站取送车作业问题一般模型，并提出了解的模块化构造方法，这虽为本问题的研究提供了新的思路，但其求解方法淡化了调机取送总时间最小的优化目标。

本文针对树枝形货物作业点取送车作业方案的优化问题，以调机前往相关货物作业点完成1批取送车作业任务为背景，以调机取送总时间、车辆的总入线车辆小时和总走行车辆公里的加权综合值最小为优化目标，以调机所连挂的车辆数不能超过其最大牵引能力和调机访问调移作业点的先后顺序为约束条件，建立兼容6种作业形式的多目标优化模型，并将其转化为单目标优化模型，运用搜索能力强的模拟退火算法进行求解，在可接受的时间范围内得到满意的取送车作业方案。

1　符号说明

定义以下参数：v0为调车场(车站)；当调机在所有作业点作业完毕返回调车场(车站)时，为便于计算机编程，此时调车场(车站)用vn+1表示。V={vi|i=1，2，…，n}为1批取送车作业涉及的货物作业点的集合。v(h)为解中第h个位置的作业点。

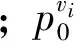
dv(i),v(j)和tv(i),v(j)分别为按文献[6]调整后的作业点vi与vj(vi,vj∈V)间的调机走行里程和调机走行时间。

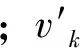
2　多目标优化模型

2.1　基本假设

(1)1批取送车作业是指调机从调车场(车站)出发，经过每个货物作业点最多1次，最后返回调车场(车站)的整个作业过程。

(2)调车场(车站)只配备1台调机负责取送车作业。

(3)各货物作业点待送、待取车数在作业前已经确定。

(4)各走行线的实际里程数、调机走行时间已知；调机附挂车辆数量的多少不影响调机在走行线的走行时间。

(5)调机将车组送至货物作业点后即离开，不需等待其装卸作业完毕后再离开。

2.2　目标函数

1)调机取送车总时间最小

调机取送车总时间是指调机离开调车场(车站)时起，至完成取送作业任务后返回调车场(车站)时止所延续的时间。调机取送车总时间最小的优化目标函数z1可表示为

(1)

2)总入线车辆小时最小

总入线车辆小时是指完成1批取送车作业时，所有送车作业的车辆在入线前消耗的车辆小时之和。总入线车辆小时越大，意味着车辆不能及时进行对位，从而有可能影响装卸作业和其他作业的及时进行，因此，总入线车辆小时的值越小越好。送车作业的车辆可分为2部分，第1部分是在调车场挑选的需送往各货物作业点的车辆，第2部分是需要调移作业的车辆，即从卸车作业点取出后送往装车作业点的车辆。

对于第1部分车辆，其总入线车辆小时为

(2)

对于第2部分车辆，其总入线辆车小时为

(3)

因此总入线车辆小时最小优化目标函数z2为以上2部分车辆的入线车辆小时之和，即

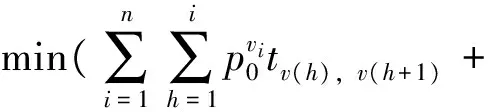
(4)

3)总走行车辆公里最小

总走行车辆公里是指完成1批取送车作业时所有车辆的走行公里之和。总走行车辆公里越大，意味着将耗费更多的调机动力，也增大了调车作业的难度，可见，总走行车辆公里的值也越小越好。因此，总走行车辆公里最小优化目标函数z3为

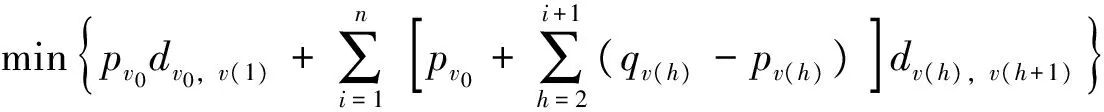
(5)

设以上3个目标的权重系数分别为α1，α2，α3；它们的取值区间均为[0，1]，且应满足α1+α2+α3=1。对于具体问题， 可采用多次实验的方法，在解比较稳定区域内选取合理的权重系数。由此可通过线性加权将树枝形货物作业点取送车作业方案多目标优化问题转化为单目标优化问题。其目标函数值z为

z=min(α1z1+α2z2+α3z3)

(6)

2.3　约束条件

1)调机牵引辆数约束

受调机牵引能力的限制，调机所连挂的车辆数不能超过其最大牵引辆数Q，即

(7)

2)调机访问调移作业点先后顺序的约束

假如1批取送车作业中存在调移作业，则调机必须首先到卸车作业点取出空车，再将其送往相应的装车作业点进行装车，所以存在调机访问这2个作业点先后顺序的约束，即

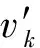
(8)

3　模型求解算法

本文建立的优化模型是一特殊的哈密尔顿图最短回路问题的数学描述，属于NP问题，采用模拟退火算法进行求解[9-11]。

采用自然数作为解的编码序列，例如某个解为0 1 3 2 4 5 7 6 8 10 9 11，表示调机从调车场(车站)出发，依次访问作业点v1，v3，v2，v4，v5，v7，v6，v8，v10，v9，然后再返回调车场(车站)。

模拟退火算法对初始解的要求并不高，可任意构造1个满足调移优先关系的解作为初始解。按照对任一调移对(vk,vk′)，在作业点vk未访问前不访问作业点vk′的原则，很容易得到初始可行解。

在开始时，退火过程的初始温度必须足够高，以确保系统能移动到所有可能的状态。

在特定温度下，当循环达到一定的上限，即马尔科夫链长度L时，必须进行降温操作。采用的退火策略为指数降温，即Tu=λTu-1(u=1,2,3,…)，其中Tu为第u次迭代时的温度，λ为温度下降率。因温度的变化很有规律，并与参数λ直接相关，即在温度高时温度下降快，在温度低时温度下降变缓，因此很适合本文所研究的问题。

解的评价可将第1个约束条件式(7)转化为惩罚函数，再将目标函数式(6)与惩罚函数的累加之和作为解的评价函数f(S)。 设M为1个足够大的正数，则调机牵引辆数约束的罚函数为

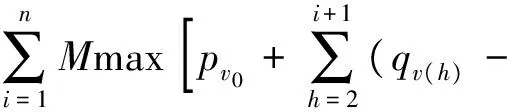
(9)

相应地，解的评价函数为

f(S)=min(α1z1+α2z2+α3z3)+

pv(h))-Q, 0]

(10)

在保证满足调移作业点访问优先权要求的前提下，为扩大解的搜索范围，依次运用以下3种方法构建新的邻域解。例如，对于作业任务要求的将作业点v2的车辆调移至作业点v4，在目前的解中，可采用如下3种方法实现。

(1) 装车点位置固定，卸车点位置前后移动。如图1所示，保持作业点v4的位置不变，将作业点v2插入到目前位置与调车场v0之间的任何位置，如v0和v3之间，或者将其插入到目前位置与作业点v4之间的任何位置，如v7和v8之间，从而得到1个新的邻域解。

图1　卸车点位置前后移动图

(2)卸车点位置固定，装车点位置前后移动。如图2所示，保持作业点v2的位置不变，将作业点v4插入到其目前位置与调车场v11之间的任意位置，如v9和v10之间，或者将其插入到取车作业点v2与目前位置之间的任何位置，如v1和v7之间，从而得到1个新的邻域解。

图2　装车点位置前后移动

(3)2—交换。如图3所示，若作业点v1和v6之间没有调移作业任务，则交换v1和v6这2个作业点的位置，就可得到1个新的邻域解。

图3　解2—交换图

算法终止条件：当温度低于某值ε时，则算法终止。

算法步骤如下。

Step 1: 选取初始温度T0，温度下降率λ，终止条件ε，马尔科夫链L，任意生成1个初始可行解S0。

Step 2: 在当前温度Tu下，对l=1,2,…,L依次运用3种邻域解的构造方法对当前解进行扰动，随机产生1个新的邻域解S′。

Step 3: 计算Δf=f(S′)-f(S)。 若Δf≤0， 则接受S′作为新的当前解， 即S=S′; 否则， 若exp(Δf/T)>rand(0，1)， 则S=S′； 否则，保留当前解S。

Step 4: 根据温度衰减函数Tu=λTu-1下降温度。判断此时温度是否满足算法终止条件；若满足则转Step 5；否则，转Step 2。

Step 5: 输出满意的取送车作业方案。

4　算　例

某铁路车站货物作业点布置情况如图4。图4中：w为道岔岔心；数字为各点(调车场(车站)、道岔岔心、作业点)间的实际里程/时间(需要说明的是，因为假定调机走行速度不变，为了计算简便明了，所以取2点间调机走行里程与走行时间相同)。1批取送车作业内容见表1；根据表1得到各货物作业点的取送车辆数见表2；按照文献[6]的方法，调整后的作业点间调机走行里程和走行时间见表3(为避免产生环，点本身间的数据取足够大的正数80)。

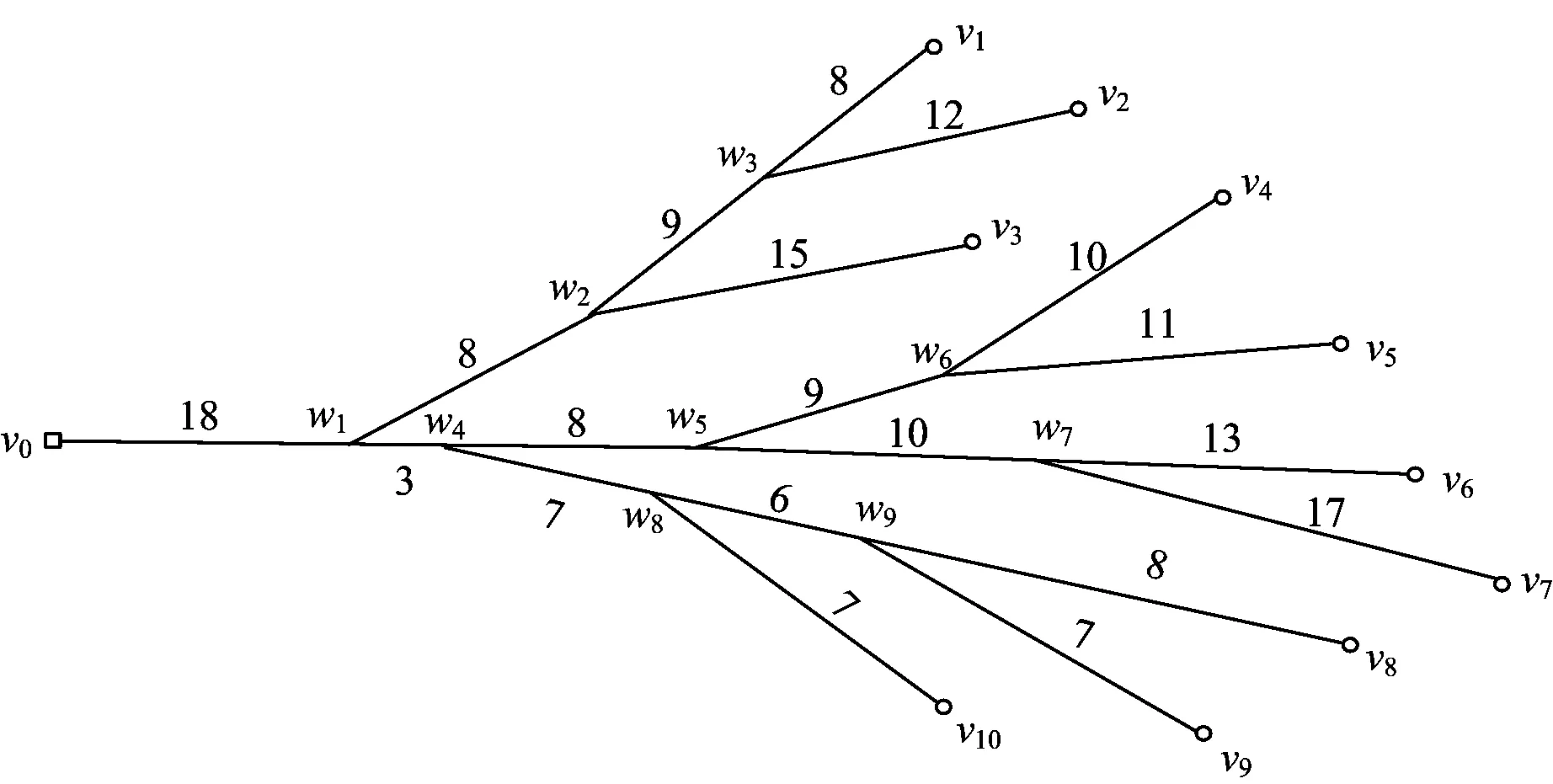
图4　某铁路车站货物作业点的布置示意图

作业点作业内容作业点作业内容v1送车2辆v6取车2辆v2取空车2辆并调移至v4v7取空车1辆并调移至v10v3取车3辆v8送车2辆v4送由作业点调移的空车2辆v9取车3辆v5送车1辆、取车1辆v10送由作业点调移的空车1辆

表2　各货物作业点的取、送车数

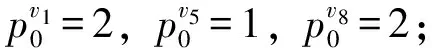
表3调车场(车站)及货物作业点间的调机走行里程/时间

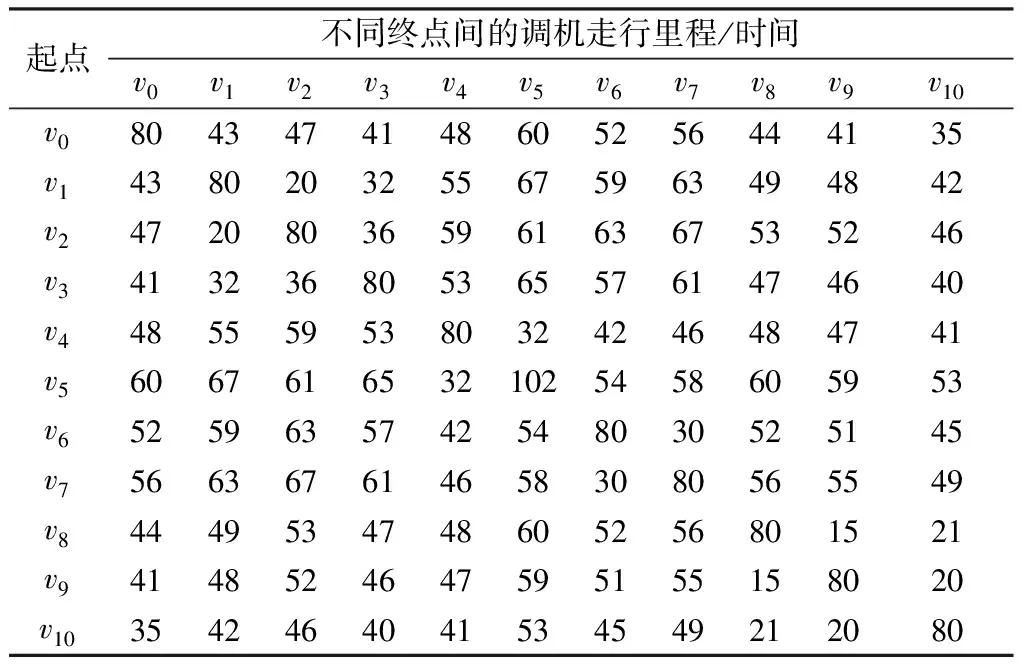
起点不同终点间的调机走行里程/时间v0v1v2v3v4v5v6v7v8v9v10v08043474148605256444135v14380203255675963494842v24720803659616367535246v34132368053655761474640v44855595380324246484741v560676165321025458605953v65259635742548030525145v75663676146583080565549v84449534748605256801521v94148524647595155158020v103542464041534549212080

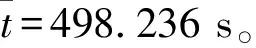
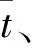
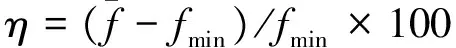
(11)

从表4可知：选取的初始温度T0越高、马尔科夫链长度L越长、终止温度ε越低，则所得到解的质量也越高；取T0=1×106，ε=0.001，L=100时，所得到解的平均质量最高，但需要37.783 s的计算时间在铁路实际运用时却略偏大。

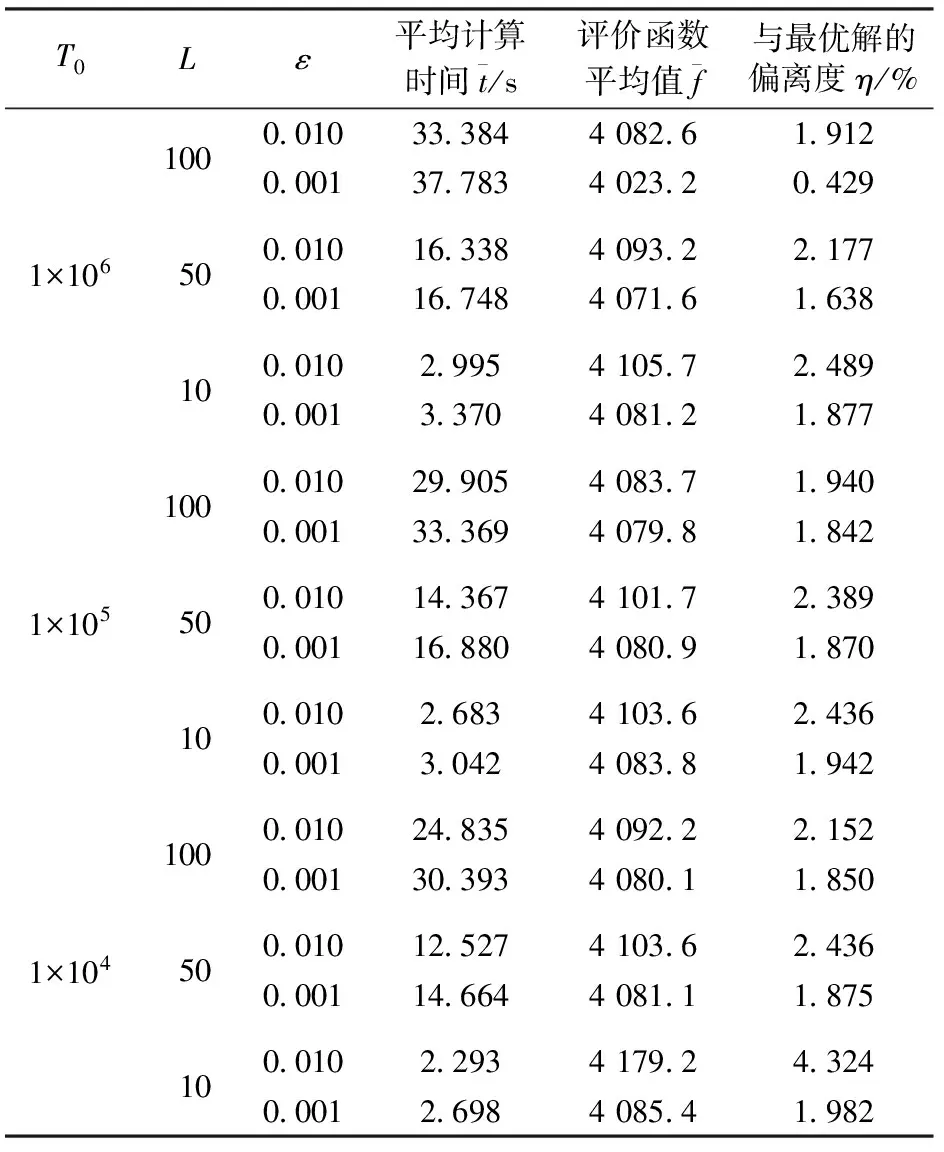
表4　参数不同取值时算法的计算结果比较

按照必须在可接受的时间范围内得到质量较高取送车方案的要求，经综合权衡，在铁路实际运用中初始温度T0可选105～106数量级的数值,终止温度ε选10-3数量级的数值；相对而言，马尔科夫链长度L对算法的计算效率影响较大，必须慎重选取，经试验认为取L=10～50较为合适。

本案例的作业任务包括了作业点的送车、取车、连送带取和调移作业等所有的作业类型，若1批取送车作业涉及更多的货物作业点，也只是增加货物作业点的数量，计算时间虽有所增加，但模型和算法是适用的，只要算法输入参数选择合理，即可实现解质量与计算效率的较好平衡。若1批取送车作业涉及的作业点较少，可认为是本文案例的简化或特殊形式，模型和算法同样是适用的。因此，本文所提出的模型和算法是有效的、合理的。

5　结　语

本文所建立的树枝形货物作业点取送车作业方案的多目标优化模型，以调机取送总时间、总入线车辆小时和总走行车辆公里的加权综合值最小为优化目标，较以往的研究成果更符合铁路车站作业实际。根据模型的特征，构造了模拟退火算法对其进行求解。将模型及算法应用于本文的案例中并多次试验表明：所建立的模型能较好地描述了取送车作业方案的编制要求和作业实际；模拟退火算法能满足模型求解和现场需求，只要选取的参数合理，解的质量和计算时间均可控制在适合运输生产需要的范围之内，从而验证了模型和算法的可行性和优越性。下一步可将取送车作业方案优化放在整个车站作业计划系统中进行研究，以服务于编制高质量的车站作业计划。

[1]石红国，彭其渊，郭寒英.树枝型专用线取送车问题的哈密尔顿图解法[J].中国铁道科学，2005，26(2):132-135.

(SHI Hongguo,PENG Qiyuan,GUO Hanying. An Algorithm by Using Hamilton Graph to Resolve Wagons’ Placing-In and Taking-Out on Branch-Shaped Sidings[J]. China Railway Science,2005,26(2):132-135.in Chinese)

[2]黄向荣.树枝形专用线取送车的模型及算法研究[J].兰州交通大学学报：自然科学版，2007，26(3): 51-54.

(HUANG Xiangrong. Model of Wagons Placing-In and Taking-Out on Brand-Shaped Sidings and the Calculating Method[J]. Journal of Lanzhou Jiaotong University：Natural Sciences,2007,26(3):51-54. in Chinese)

[3]郭垂江，雷定猷.铁路车站取送车作业图论模型及算法分析[J].华东交通大学学报，2014，31(1)：102-107.

(GUO Chuijiang,LEI Dingyou.Model and Algorithm of Wagons’ Placing-In and Taking-Out in Railway Station[J].Journal of East China Jiaotong University,2014，31(1)：102-107. in Chinese)

[4]杨运贵，王慈光，薛锋.树枝形铁路专用线取送车问题的遗传算法研究[J].计算机工程与应用，2008，44(12):210-211,214.

(YAN Yungui,WANG Ciguang,XUE Feng. Study on Genetic Algorithm for Railway Placing-In and Taking-Out of Wagons in Branch-Shaped Private Siding[J].Computer Engineering and Applications,2008,44(12):210-211,214.in Chinese)

[5]GUO Chuijiang, LEI Dingyou. Model of Wagons’ Placing-In and Taking-Out Problem in a Railway Station and Its Heuristic Algorithm[J]. Mathematical Problems in Engineering， 2014(8):1-8.

[6]郭垂江，雷定猷.树枝形铁路专用线取送车作业模型及启发式算法[J].铁道科学与工程学报，2015,12(1)：208-213.

(GUO Chuijiang,LEI Dingyou. Wagons’ Placing-In and Taking-Out Model in Branch-Shaped Railway and Its Heuristic Algorithm[J].Journal of Railway Science and Engineering, 2015,12(1)：208-213. in Chinese)

[7]王慈光.运输模型及优化[M].1版.北京:中国铁道出版社,2004：15-21.

[8]牟峰, 王慈光, 牟从凯. 铁路车站取送车作业问题一般模型解的构造方法[J].中国铁道科学，2012，33(5):105-113.

(MU Feng,WANG Ciguang,MU Congkai.A Method for Generating Solutions of the Generic Model for Taking-Out and Placing-In Wagons in Railway Station[J]. China Railway Science,2012,33 (5):105-113.in Chinese)

[9]李金忠，夏洁武，曾小荟,等.多目标模拟退火算法及其应用研究进展[J].计算机工程与科学，2013，35(8):77-88.

(LI Jinzhong,XIA Jiewu,ZENG Xiaohui, et al. Survey of Multi-Objective Simulated Annealing Algorithm and Its Applications[J].Computer Engineering & Science,2013，35(8):77-88. in Chinese)

[10]SUMAN Balram. Study of Simulated Annealing Based Algorithms for Multi-Objective Optimization of a Constrained Problem [J]. Computers & Chemical Engineering，2004,28(9):1849-1871.

[11]SUMAN B, Kumar P. A Survey of Simulated Annealing as a Tool for Single and Multi-Objective Optimization[J]. Journal of the Operational Research Society,2006,57:1143-1160.