估算在数学解答题中的应用

屈润华

(新疆和田地区教育学院，新疆 和田 848000)

估算在数学解答题中的应用

屈润华

(新疆和田地区教育学院，新疆 和田 848000)

本文通过例子介绍利用估算解答数学大题的一些方法，对数学专业的学生有一定的指导意义。

估算；近似计算；解答题

一、估算介绍

所谓估算，就是根据一定的条件，按照某种要求，对结果确定一个范围或给出一个近似的估计。估算不仅是近似计算，更是一种方法，一种思想，是基于问题条件，对所求的结果进行预判、调整、逼近、验证等。《数学课程标准》指出:“估算在日常生活与数学学习中有着十分广泛的应用,培养学生的估算意识,发展学生的估算能力,让学生拥有良好的数感,具有重要的价值。”《新课程标准》要求学生在解决具体的问题过程中，能选择合适的估算方法，养成估算的习惯。然而估算是比精确计算更高的一种思维形式,本文通过一些中小学的解答题，从范围、能算、好算、简单、比较等角度，介绍估算的方法,使学生能快速找到解题的的突破口，从而提高解题的能力。

二、例题讲解

(一)范围

例1 一个四位数与它的各个数位上的数字和的和是2091，求这个四位数。

分析：设这个四位数是a,它的各个数位数字和是b,则a+b=2091。此方程有两个未知数，正整数解很多。但a,b都有范围，利用b的范围在1和36之间，变化相对少，则a介于2055和2090之间。于是a的头两位是20，不难得到a是2076。

(二)能算

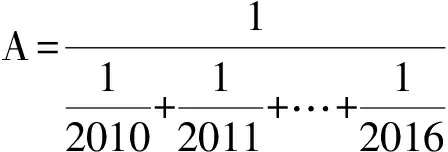
(三)好算

例3 三个相邻偶数之积为首位是8末尾是2的六位数，求这三个数。

分析：先作个位数字分析，偶数的个位数字是0，2，4，6，8。由三相邻偶数乘积的个位为2，知这三个偶数的个位数字只能是4，6，8。对这样的相邻三偶数乘积做好算估计，由1003=1000000，903=729000,知这三个偶数只能是94，96，98，它们的乘积是884352，因而它们就是所求的三个数。

(四)简单

例4 在下列等号左端填上运算符合，使等号成立：8 8 8 8 8 8 8 8 8 8=2000。

分析：因2000=16×125有16的因数，按估算小数比估算大数简单的原则，我们用两个8得到16，故只需用8个8的运算使之等于125。通过最少个数的8的运算估算125，不难得到8×(8+8)=128。剩下由5个8的运算得到3，这是容易做到的。故有(8+8)×(8×(8+8)-(8+8)÷8-8÷8)-2000。

(五)比较

例5 在图一中，正方形内的阴影部分的面积是53，则正方形的面积是多少？

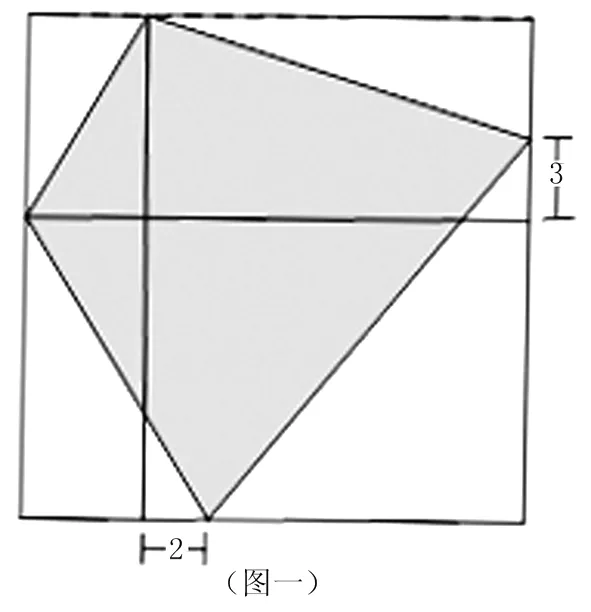
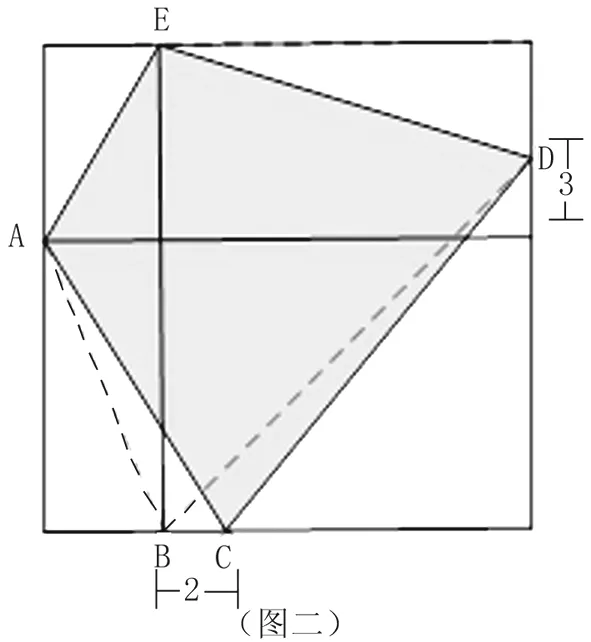
分析：如图二所示标记符号。阴影部分为四边形ACDE，它的四个顶点中有两个点C和D不规则。连接AB、BD，考虑仅一个点不规则的四边形ABDE，用它的面积来估算阴影部分面积。

注意到四边形ABDE的面积与它外面的四个三角形的面积和相等，因而都是正方形面积的一半。阴影部分面积与四边形ABDE的面积差是三

角形DBC与三角形ABC的面积差；而三角形DBC与三角形ABC的底相同，为2，高相差3，即面积相差2×3÷2=3。所以正方形的面积是(53-3)×2=100。

三、结束语

估算的思想和能力在学生的学习过程中占有相当重要的地位和作用，估算的途径是有规律可循的，只要我们在教学中重视加强估算教学，有目的的培养学生的估算意识，就一定能发展学生的估算能力，使学生拥有良好的数感，提升学生的数学素养。

估算作为一种解题的方法和策略，它并非万能的，只有针对特定的题目和相应的题型，估算才有实施的可能。估算的策略并非一种无中生有的猜测，而是在对数学知识、方法、能力具有了一定高度之后的一种必然的意识和能力。我们研究估算的应用途径，也重在熏陶学生的估算意识，一种将数学思想方法应用于实践及实际生活的意识，这也是现代数学教学理念的根本所在。

[1]马永和.估算法在数学解题中的应用[J].中学数学，2001:(08).

[2]彭霞.估算在解数学题中的应用[J].高中数理化,2005(02).

[3]黄益全.估算在高中数学解题中的应用[J].中学数学教学参考(高中)，2007(07)。 [4]应立君、张淼.估算在数学竞赛中的应用[J].中学教研，2009(6).

2016-12-20

屈润华，新疆和田地区教育学院(师范学校)数学专业教师。