基于全局搜索算法的太阳影子定位研究

孙慧宇，贺小龙，吴 飞

(1.安徽财经大学金融学院，安徽 蚌埠 233030；2.安徽财经大学管理科学与工程学院，安徽 蚌埠 233030； 3.安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

基于全局搜索算法的太阳影子定位研究

孙慧宇1，贺小龙2，吴 飞3

(1.安徽财经大学金融学院，安徽 蚌埠 233030；2.安徽财经大学管理科学与工程学院，安徽 蚌埠 233030； 3.安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

目的 为更好地解决已知某物体影长、测量的时间和日期的情况下确定物体的测量地点，或已知物体影长、测量日期及地点的情况下确定测量时间的问题，进而解决野外探险时地理位置的确定和根据某物体的视频或照片等影像资料而确定其拍摄地等实际问题。方法 针对太阳影子定位，使用基于穷举法的全局搜索式算法、最小二乘法的参数估计法、比例消参法等方法，分别构建全局搜索网络模型、参数方程模型等模型，结合MATLAB软件进行算法的编写、图形的绘制、数据的拟合与预测等处理。结果 结合第一组数据，所推算的测量地位于广西，结合第二组数据，所推算的测量地在蒙古国。结论 利用全局搜索式算法及参数方程模型，结合MATLAB软件，可以解决太阳影长、直杆长度、测量地点、测量日期、测量时间等5个变量中知四求一、知三求二等问题。

太阳影子定位；全局网络搜索；测量；MATLAB

0 引 言

物体在灯光或自然光线的照射下会产生影子并且影子的长度会因为某些因素发生改变，但是如何确定太阳影子的作用机制并根据其中多个未知量进行计算而求得其他几个未知量并没有深入的研究，而太阳影子定位可广泛应用于野外求生、刑事侦查、军事侦察以及科研计算中，因此，对太阳影子及其影响机制以及相互递推关系进行探讨显得尤为重要。

1 太阳影子的影响机制

为分析不同因素对于物体影长的影响机制并建立相应的数学模型来反映这种影响机制，同时利用所建立的模型绘制2015年10月22日北京时间9∶00～15∶00北京天安门广场3 m高的直杆的太阳影子变化曲线,并以此为例。明确太阳高度角α、测点纬度φ、太阳赤纬σ以及太阳时角t等参数，参考三角函数表，对太阳影子长度的变化机制做出评价并绘制相应的曲线[1]。

1.1 数据处理

(1)太阳赤纬σ：表示太阳光线与地球赤道面的夹角，一年四季每天都在变动着，冬至日σ=-23 °27′，春分日和秋分日σ=0 °，夏至日σ=23 °27′。若定义每年的1月1日日期序数为1，且之后的每一天日期序数依次递增，则结合相关资料可得太阳赤纬计算公式：

例如太阳赤纬为-15 °13′，即太阳直射15 °13′S。

(2)太阳时角t：t为太阳时角，以当地正午为0 °，上午为负，每后退1小时减15 °，下午为正，每前进1小时加15 °，仅以t表示太阳时。例如北京时间9∶00～15∶00的太阳时角为-45～45 °，每分钟变化0.25 °。

(3)太阳高度角α：太阳高度角即为太阳入射光线和地面切线的夹角(见图1)，其中α为太阳高度角，I1为太阳入射平行光线，I2地面切线，通过查阅相关资料[2]可得太阳高度角计算公式：

sinα=sinσsinφ+cosσcosφcost

(1)

其中α为太阳高度角、φ为测点纬度、σ为太阳赤纬，t为太阳时角。

1.2 确定参数变量关系

将太阳高度角、杆长以及影长的互相影响抽象为几何问题，可得影长示意图(图2)。[1]

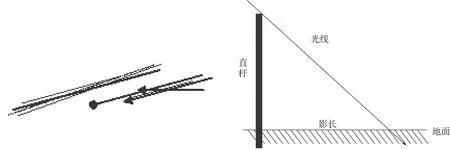
图1 太阳高度角示意图 图2 影长示意图

据此可得杆长、影长以及太阳高度角之间的关系：

(2)

其中l为影长，h为杆长，α为太阳高度角。

结合公式(1)和公式(2)可得影响物体影长与太阳时角、测点纬度、太阳赤纬以及杆长的参数函数：

(3)

其中:太阳赤纬、测地纬度、太阳时角保持不变时，则影长随杆长的增加而增加；

杆长、测地纬度、太阳时角保持不变时，则太阳直射点离测量地越远，影长越短；

杆长、太阳赤纬、太阳时角均保持不变时，则测量地离太阳直射点越远，影长越短；

杆长、太阳赤纬、测地纬度均保持不变时，则当太阳时角小于零时，影长随太阳时角的增大而减小，当太阳时角大于零时，影长随太阳时角的增大而增大。

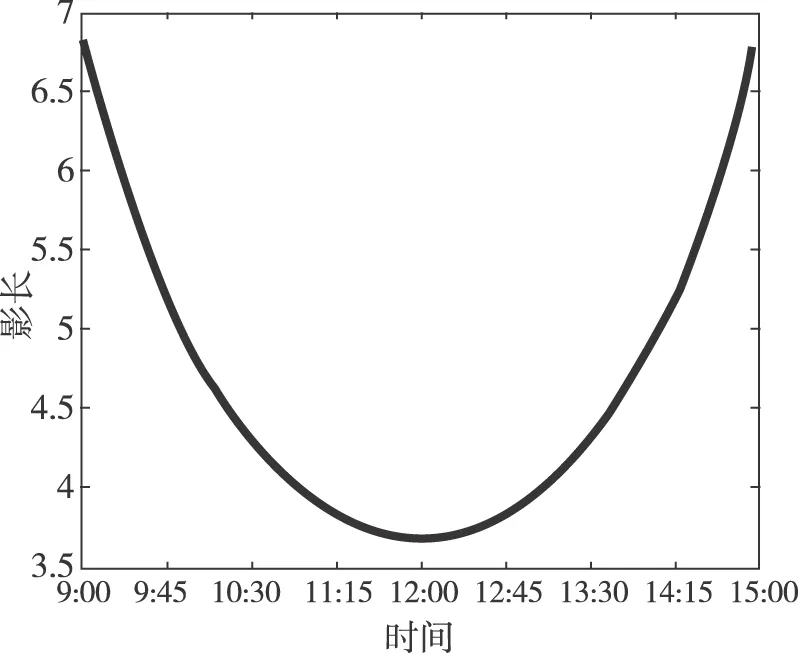
图3 直杆的影长随时间变化图

以2015年10月22日北京时间9∶00～15∶00时北京天安门广场3m高的直杆为例，利用太阳影子图像的绘制，结合影子定点坐标，利用MATLAB软件可绘制其图像(见图3)。

2 太阳影子影响因素中单因素未知求解方法

根据平面上影子的顶点坐标求解出影子的长度，从而针对时间以及影长进行拟合[3]，进而预测北京时间14∶42时之前的时点在观测地点直杆的影子长度，因为正午时刻影子是一天中最短的时刻，所以通过所拟合的函数顶点来推测测量地的正午时刻所对应的北京时间，从而通过时间差来计算两地经度差，进一步确定观测地点的经度；针对观测点纬度，结合公式(3)及附件(1)[4]中的数据通过计算不同时刻的影长并构建比例消元模型以消除杆长对计算的影响，进而对以测地纬度为未知量一元线性方程进行求解，最终得到观测点的经纬度数据。

2.1 数据的处理

(1)相关数据的获取

通过观察和测量，得到太阳影子的定点坐标(见表1)。

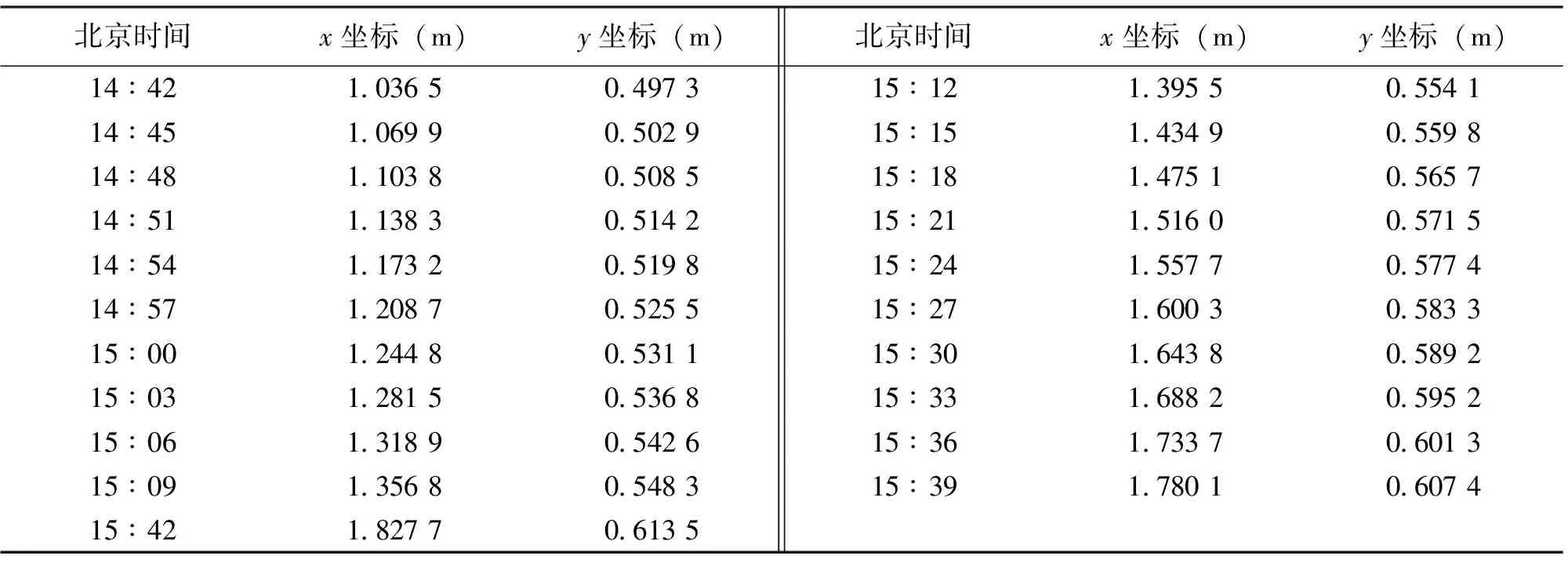
表1 直杆影子定点坐标表

(2)观测地经度的数据准备

图4 直杆影长示意图

根据文献[4]中的数据利用Excel进行二次拟合,可得到北京时间14∶42～15∶42时之间的影长与时间的函数关系：

y=0.0004x2+0.0305x+1.12083

(5)

其中定义北京时间14∶42时刻为x=1，此后时间每增加3min，x的值便增加1；同理，时间每减少3min，x的值便减少1。通过MATLAB绘制函数曲线进行预测可得到直杆影长示意图(见图4)。

利用MATLAB数据游标工具不难得出该曲线的最低点为(-38,0.538 9)，即北京时间为12∶45时影长最短，为0.538 9m。由影长变化规律[5]可知，北京时间为12∶45时测量地的时间为正午12∶00时，因此测量地与北京存在45min的时差，即可求得测量地的经度约为东经109°10′。

2.2 求解方法

根据表1提供的21组不同时间对应的影子坐标，计算出相应的影子长度h，再根据公式(3)，在21组数据中任意选取2组数据进行比例消元，可以得到如下公式：

其中每天求的太阳赤纬[6]是一样的，并且知道日期，可以根据太阳赤纬公式y=23.45×sin(360×(284+n)/365)求出每天相应的赤纬角度。其时角也可以根据不同时间对应求出，最后模型中只剩下测量地的纬度是未知的。

2.3 结果及分析

为了消除杆长未知对计算结果的影响[7]，选取文献[4]14∶45时与15∶15时2个时点为例，从而构建比例式以求解测地纬度。计算结果：

(6)

图5 影长比例图

利用MATLAB绘制图像(见图5)。

利用MATALB数据游标工具可知当x分别取-1.244、0.018 14、0.337 4时公式(6)成立，此时的测地纬度为南纬71.312 °、南纬1.040 °、北纬19.341 °。通过计算可得到剩余9组数据，通过查阅相关经纬度即可确定观测地，经整理可得观测地时间、零点x值、影长比、纬度汇总表(见表2)。

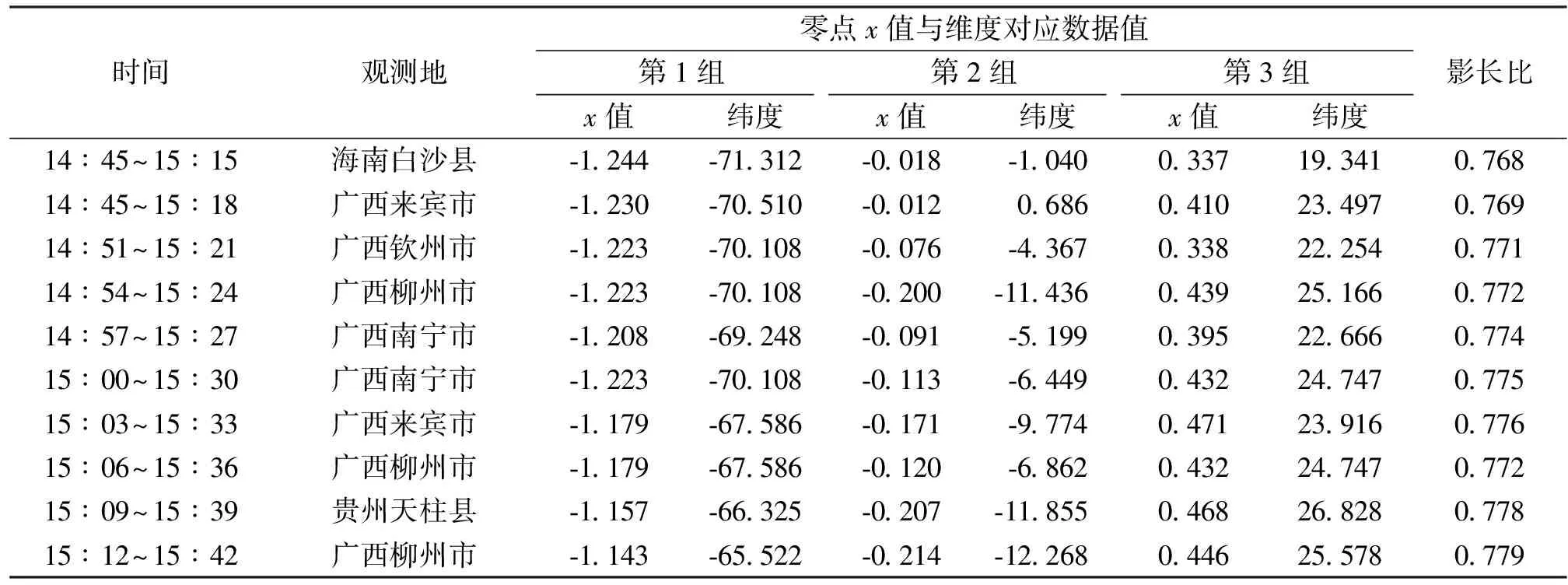
表2 观测地对应数据汇总表

根据附件(1)[4]给出的影子坐标，结合相关数据求得可能的观测点为广西、海南、贵州。其中广西省的频数为8，因此推断最可能的观测地点是广西省。

3 太阳影子影响因素中双因素未知求解方法

根据平面上影子的顶点坐标求解出影子的长度，建立基于“最小二乘法”[8]的数据拟合模型。根据时间关系对影长进行拟合，进而求出影子最短时的时间。再根据正午时刻影子最短原理[9]，通过拟合函数推测出测量地的正午时刻对应的北京时间，从而根据时间差来计算两地经度差。针对观测点纬度，建立基于“穷举法”的全局搜索算法模型，利用穷举法分别对杆长、日期、纬度进行三层循环遍历[10]，利用公式(3)求出相对应的影长，将求出的影长于实际影长的差的绝对值进行累加，最后比较累加值[11]，最小的累加值相对应的纬度和日期即为所需要求的纬度和日期。

3.1 数据处理

(1)经度求解的数据准备

通过观测可获得一组太阳影子顶点坐标并对其进行整合后计算影子长度(见表3)。

表3 观测地坐标及对应影子长度汇总表

注:定义x=1对应文献[4]中的起始观测时刻，时间每增加3min，x的值增加1。

(2)纬度求解的数据准备

a.杆长h:假设杆长的范围为0.1～10 m。

b.太阳赤纬y:定义每年的1月1日的日期序数为1进行编号(忽略闰年的影响)，其最大值为365。通过求太阳赤纬的公式y=23.45×sin(360×284+n)/365)

推算出相应的赤纬角度y。

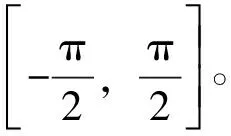
d.太阳时角θ:定义太阳时角的计算公式为θ=15×(t-12)，其中t表示测量地的测量时间与零时的差值，单位以小时计。再结合文献[4]中给出的时间和前述结论中已求得的经度推算出测量地的即时时间，就可以准确算出太阳时角[12]，其中上午的太阳时角为正，下午的太阳时角为负。

3.2 求解方法

在经度求解方面，可采用本文太阳影子影响因素中单因素未知求解中的方法求解。在纬度求解时，引入基于穷举法的全局搜索式模型，将求杆长所需要的4个参数，杆长、太阳赤纬、测地纬度和太阳时角，根据实际经验和理论上数据分别对其赋值遍历，求出估计杆长。再将求出的估计杆长与文献[4]的实际杆长作差，将21组数据的差的绝对值累加。对每组数据的累加结果进行比较，其中误差最小即累加值最小，对应的杆长、太阳赤纬、测地纬度和太阳时角即符合条件。

3.3 结果分析

针对经度求解可利用MAYTLAB绘制其拟合图像并推测经度(见图6～图9)。

图6 影子长度的散点图 图7 影子长度的拟合曲线图

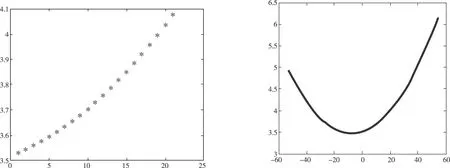
图8 影子长度的散点图 图9 影子长度的拟合曲线图

针对2组数据分别得出如下结论：第一组数据中日期序列序号n=71，即3月12日，杆长h=1.5 m，纬度为38度,结合API坐标反查与所求得的经度可知其测量地点大约在新疆维吾尔自治区。

第二组数据中日期序列序号n=294，即10月21日，杆长h=1.5 m，纬度为46 °，结合API坐标反查与所求的得经度可确定其测量地点大约在蒙古国。

4 结 论

在太阳影子影响机制方面：建立的太阳影子影响机制模型：

并以此模型为蓝本，通过比例消元、参数估计以及基于穷举法的全局搜索算法等方法，针对不同的观测数据可以做到知四求一甚至知三求二。即测量地、测量时间、测量日期、物体影长和直杆长度中3个或3个以上为已知时，剩余变量可以求解得出。

[1]Wu L,Cao X C,Foroosh H.Camera calibration and geo-location estimation from two shadow trajectories[J].Comput Vis Image Underst,2010,114(08):915-927.

[2]Junejo I,Foroosh H.GPS coordinates estimation and camera calibration from solar shadows[J].Comput Vis Image Underst,2010,114(09):991-1003.

[3]屈名，王征兵，王德麾.基于交比不变性的太阳定位算法的研究[J].Silicon Valley,2013,(19):53-55.

[4]中国工业与应用数学学会，2015全国大学生数学建模竞赛A题[EB/OL].http://www.mcm.edu.cn/html.cn/node/ac8b96613522ef62c019dlcd45a125e3.html.2015-09-14.

[5]林根石.利用太阳视坐标的计算进行物高测量与定位[J].南京林业大学学报,1991,15(03):89-93.

[6]姚宋涵，王殿海，曲昭伟.基于二流理论的拥挤交通当量排队长度模型[J].东南大学学报：自然科学版，2007,37(03)：521-526.

[7]陈佳.周涛.曾祥平.城市异常路段交通拥挤——消散分析[J].中国水运，2007,7(02)：63-64.

[8]吴正.高速公路交通事故和干涉车流波的非线性数学模型[J].西安公路交通大学学报，2001,21(02)：77-80.

[9]洪文，冯守平，吴本中.利用LINGO建立最优化模型[M].长春：吉林大学出版社，2005:4-59.

[10]郭耀煌，钟小鹏.动态车辆路径问题排队模型分析[J].管理科学报,2006，9(01)：34-37.

[11]何原标.用天文年历进行表差和经度计算[J].测路通报1983,(06)：11-12.

[12]肖智勇,刘宇翔.一种新的纬度测量方法[J].大学物理，2010,29(09):51-54.

[责任编辑：关金玉 英文编辑：刘彦哲]

Orientation of Sun Shadow Based on Global Search Algorithm

SUN Hui-yu1,HE Xiao-long2,WU Fei3

(1.School of Finance,Anhui University of Finance and Economics,Bengbu,Anhui 233030,China;2.School of Management Science and Engineering,Anhui University of Finance and Economics,Bengbu,Anhui 233030,China； 3.School of Statistics and Applied Mathematics,Anhui University of Finance and Economics,Bengbu,Anhui 233030,China)

Objective To work out where the measurement locates with the known length of the shadows and the date of survey or the date of survey with the known length of the shadows and where the measurement locates,thus ensuring the position with a known wild adventure and the measurement address according to a photo or video.Methods Aiming at the orientation of sun shadow,based on global search algorithm,the return model parameter estimation by ordinary least squares and maximum likelihood,and the bias elimination,the global search network model,and parameter equation model were establish.By using MATLAB,the algorithm writing,graphing,data fitting and predicting were conducted.Results Combing with the data of group 1,the result was Guangxi Province;as for the question 2,the answer Mongolia.Conclusion By using the parameter equation model,global search algorithm and MATLAB,the length of the shadow,the length of the pole,the measuring location,the data of survey and the time of survey can be worked out.

sun shadow positioning;global web search;measurement;MATLAB

教育部人文社会科学青年科研资助项目(10YJC630143)

孙慧宇(1994-)，女，江苏南京人，安徽财经大学金融学院在读学生，研究方向为应用数学。

朱家明(1973-)，安徽泗县人，副教授，硕士，研究方向：应用数学与建模。

TP 242.6

A

10.3969/j.issn.1673-1492.2017.01.004

来稿日期：2016.04.05