基于高斯模型对京津冀地区空气污染的研究

张德鑫，陈 春，朱 晗，余 湉

(安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

基于高斯模型对京津冀地区空气污染的研究

张德鑫，陈 春，朱 晗，余 湉

(安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

目的 针对京津冀地区空气质量指数和污染源，在国标(AQI)基础上改进并建立新的空气质量标准来定义空气等级标准。方法 建立合理模型对污染源的扩散类型进行研究，使用模糊C均值聚类、模糊综合评价、F检验，分类讨论等方法，分别构建空气质量优劣衡量体系、连续高架点源高斯扩散、瞬时高架点源高斯扩散、连续线源高斯扩散等模型，使用MATLAB、SPSS软件，得到影响空气质量的关键参数。根据从离散到连续的思想，利用积分，建立线源高斯扩散模型。再依照中国《环境空气质量标准》确定垂直扩散参数分析北京二环四环与六环的空气污染浓度。结果 结果显示：四环的污染物浓度最高，其次是二环，最末是六环，浓度从8∶00到21∶00顺次递减;将限行前后数据比对分析可得，所有路线污染物浓度均显著下降，故限行政策效果显著。结论 分析得出京津冀地区污染的主要原因分别是机动车的大量使用、工业的废气排放以及煤炭与油等化石能源的燃烧等结论。最后给出治理京津冀地区空气污染的建议。

高斯模型;空气污染;模糊聚类;综合评价;F检验

0 引 言

近年来，中国经济快速增长，同时也带来了严重的环境问题。这其中，空气污染严重影响人类生产生活，是影响人类健康的一个主要环境风险。18世纪产业革命后，煤和石油等燃料的燃烧大量增加，空气污染随之加剧，导致一系列人类呼吸系统疾病和心血管疾病等问题，人类才开始真正意识到大气污染的严重性。通常用空气质量指数(air quality index，AQI)来定量描述空气质量状况，并划分空气质量等级，中国国家标准和美国国家标准对划分的指数上限浓度略有差异，并且针对单项污染物还规定了空气质量分指数。参与空气质量评价的主要污染物为细颗粒物PM10、可吸入颗粒物PM2.5、二氧化硫、二氧化氮、臭氧、一氧化碳。

人类生产、生活排放大量大气污染物，导致城市空气污染日益加重，而京津冀地区的空气污染问题尤为严重，据中国环保部发布的报告2013年6月京津冀地区空气质量重度污染以上天次占21.2%。因此需要建立一个空气质量评价数学模型来评价各地区各时点的空气质量状况，分析其主要污染源的性质和种类，以便做出正确的出行选择以及在一定程度上改善和治理空气污染(详见2015年五一数学建模联赛B题[1])。

1 空气质量优劣程度等级的判别

1.1 研究思路

以京津冀地区为研究对象，参考国标[2]和美标建立衡量空气质量优劣程度等级的数学模型。河北省以石家庄作为代表，从气象部网站调取2014年7月、10月和2015年1月、4月4个月份的6号、16号、26号北京、天津、石家庄的空气质量情况相关指数共36组数据作为样本并依次排序，对这些样本进行聚类分析得到衡量空气质量优劣程度等级的数学模型。

1.2 模糊C均值聚类

首先，运用MATLAB软件对样本中的数据进行模糊C均值聚类，得到结果见表1。

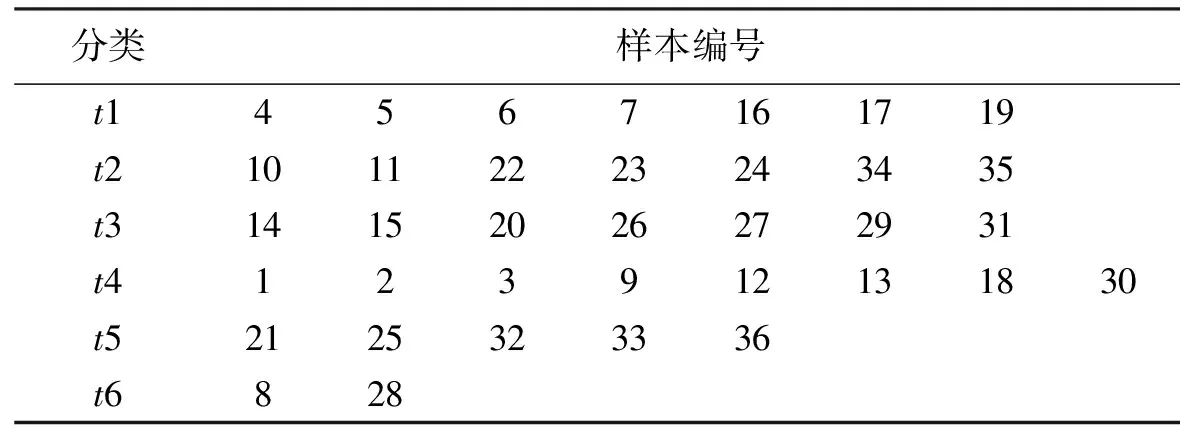
表1 MATLAB模糊C均值聚类结果

注：其中，t1至t6表示将样本分为6类，其后的数值代表样本的序号。

然后运用SPSS软件对分类的结果做Friedman检验，检验水平为α=0.04，分别采取各类别之间检验与其中两类合并以后检验，显然各类别之间的检验接受原假设比其中两类合并后检验接受原假设的要多，这说明各类之间差距较大，同一类中个体之间差异较小，结果符合聚类的基本原则。

1.2.1 构建空气质量等级标准

通过对聚类结果的检验和分析，将分成的6类结果人为定义为优、良、轻度污染、中度污染、重度污染和严重污染6个空气质量优劣程度等级，再对其每个等级的各参数指标数据进行如下处理：

在a、b、c中选取合适的数值代表每个空气质量等级的各指标所在范围，注意同一指标的上下范围要连贯，得到如下空气质量优劣程度等级划分(见表2)。

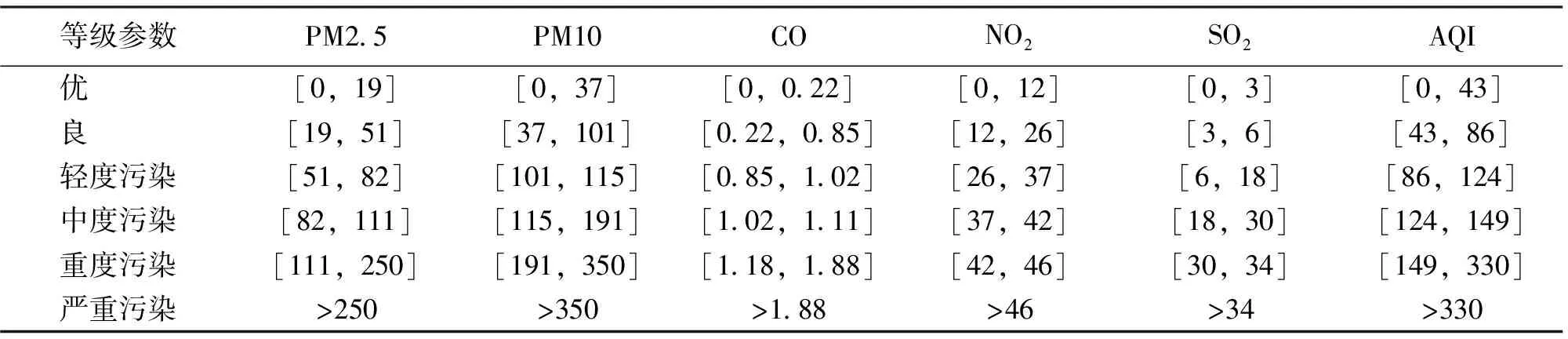
表2 空气质量等级标准(μg·m-3)

运用公式：

其中，I为空气质量指数，即AQI，是输出值；C为污染物浓度，输入值；Clow表示小于或等于C的浓度限值；Chigh为大于或等于C的浓度限值；Ilow是对应于Clow的指数限值；Ihigh是对应于Chigh的指数限值，Clow、Chigh、Ilow、Ihigh皆为常量。利用这个公式，根据污染物浓度C，可以方便地计算出空气质量指数I，再与表1相对照，判断其空气质量属于何种等级。

1.2.2 模型的检验

假若给定某城市某日24时各污染物平均浓度，即可按照已建立的模型算出其AQI，再根据空气质量等级标准表对照判断出其空气质量状况如何，通过按照国标和美标的标准计算其空气质量指数AQI与表2中的国标和美标浓度限值相对照，检验其结果的正确性。

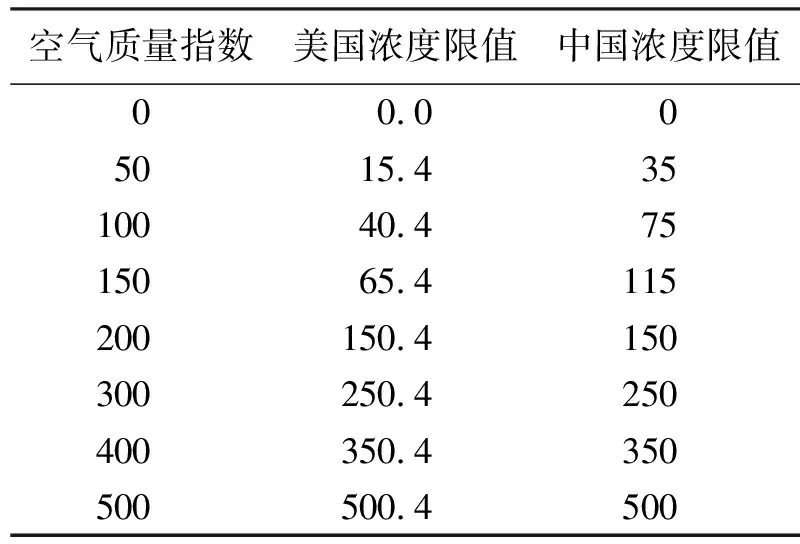
表3 国标和美标污染物浓度限值

2 不同污染源下空气污染扩散研究

2.1 连续高架点源高斯扩散模型的建立

2.1.1 相关指标公式

公式I瞬时污染气体排放量

瞬时污染气体排放量指的是排放一段时间污染气体后短时间内不再排放的情况，假设排放的气体不发生任何化学反应且没有其它气体的混入时，将之前排放量看作是接下来一段时间内的瞬时排放量，即：

Q=CVΔt

公式Ⅱ 单位时间污染气体排放量

点源污染气体的排放是连续的，用单位时间污染气体的排放量来研究对浓度的影响，即：

公式Ⅲ 烟羽抬升高度估计

烟羽抬升是指烟气离开排放源后因初始动力和热力作用而继续上升并逐渐变平的过程[3]。烟囱排出的烟气有一定的出口速度，温度也高于出口处的环境大气。这样烟流在动力和热力的作用下，在一定条件下可抬至相当的高度，之后在空气阻力和重力的作用下沿风的方向变平。查阅有关文献可知，其标准公式：

Δh=2(1.5VD+0.04QH)u-1

式中，V表示烟气出口速度(立方米每时),D表示烟囱口内径，QH为排热量(千卡/秒)，u表示烟囱顶处的平均风速(米每秒)。

公式Ⅳ 污染源有效高度

污染源的有效高度包括烟囱的实际高度和烟羽抬升高度：

H=H0+Δh

2.1.2 建立模型

假设污染气体排放的过程中不被吸收且未发生化学反应。以有效污染源为坐标原点，风向所指方向为X轴正方向，构建空间坐标系。污染气体沿X轴向横侧和垂直方向自由扩散，假设Y轴、Z轴上浓度分布服从二维正态分布。先从不考虑地面障碍物着手，对下风向点浓度建立高架点源高斯扩散模型，再结合形象图利用镜像对模型进行完善，构建下风向点浓度函数。而在点源的实际扩散过程中，污染气体可能会受到地面障碍物的影响。在凌晨5时至上午8时和下午16时至晚上21时这2个时间段上不再排放污染气体，可将其看成瞬时排放，构建瞬时高架点源高斯扩散模型。而早上9时至下午15时、晚上22时至凌晨4时2个时间段上污染源连续排放污染气体，对其构建连续高架点源扩散模型[4]。最终将数据代入模型进行求解，根据各个下风向点浓度可知空间污染浓度分布，再对照空气质量指标可判断出空气质量等级。

2.1.3 模型的建立

1)不考虑地面障碍物的影响

a.下风向点浓度分布和空间坐标以及单位时间排放量有关，构建浓度函数：

C=C(X,Y,Z,t)

b.以有效污染源为坐标原点，风向所指方向为X轴正方向，建立三维空间坐标系。污染气体沿着X轴横向、垂直自由扩散，单位时间内对下风向点浓度函数进行积分等于单位时间内的污染气体排放量：

c.假设污染气体沿X轴，随风向Y轴、Z轴方向上自由扩散相互独立且服从二维正态分布。在不考虑地面障碍物的影响下μy=0,μz=0,可构建二维正态分布密度函数，并化简可得风向点浓度函数：

(1)

2)考虑地面障碍物的影响

a.假设有效污染源位于与地面相距H处，以有效污染源为坐标原点，风向所指方向为X轴正方向，建立三维空间坐标系。假设下风向点K位于离地面z处，根据不考虑地面障碍物影响下风点浓度密度函数可知：

b.由于考虑地面障碍物的影响，部分气体从始源出发扩散碰到地面发生全反射，又折回地面上空，刚好到达下风向点K。2次浓度发生叠加，即区别于不考虑地面障碍物的影响。而叠加上去的浓度相当于将有效污染源关于地面的镜像点为污染源，不考虑地面障碍物影响自由扩散到下风向点K的浓度，K点在Z轴方向上坐标为(z+H)，可得叠加上去的浓度：

由此可知，考虑地面障碍物影响下风向点K的浓度函数：

(2)

2.2 建立瞬时高架点源高斯扩散模型

2.2.1 模型的分析与构建

与2.2模型的构建思路相同，唯一的区别就在于对某一时间点上的下风向点浓度进行积分等于瞬时污染气体排放量且烟羽抬升高度为零，因此按照2.2模型的思路可构建瞬时高架点源高斯扩散模型，求得考虑地面障碍物影响下风向点K的浓度函数：

(3)

2.2.2 模型的参数估计与求解

1)扩散参数σy,σz的估计

查阅有关文献，中国GB3804-91《制定地方大气污染物排放标准的技术方法》[2]采用如下经验公式确定扩散参数σy、σz：

σy=γ1Xα1,σz=γ2Xα2

式中，γ1、α1、γ2,α2称为扩散系数。这些系数由实验确定，在一个相当长的X距离内为常数，可从GB3804-91文献的表中查取[2]。

2)烟羽抬升高度估计

假定该工厂的烟囱内径为d(m),排热量为qh(kcal·s-1)，以烟囱出口处的环境风速us(m·s-1)估计烟囱顶处的平均风速。问题三中要求解的各个时点上的烟气出口速度各不相同,由于早上8时、中午12时、晚上21时的烟气出口速度分别为V1=0 m3·h-1,V2=1 200 m3·h-1,V3=0 m3·h-1，代入公式可得早上8时、中午12时、晚上21时的烟羽抬升高度分别：

3)各时点污染浓度函数

早上8时属于凌晨5时至上午8时，符合瞬时高架点源高斯扩散模型,排放浓度C1=1 160 mg·m-3、排放速度为V1=5 700 m3·h-1、间隔时间Δt=9 h、在下风距离X=51 000 m、烟囱高H0=50 m，将数据代入公式(3)即可求解出下风向点浓度函数，如下：

中午12点属于上午9时至下午15时，符合连续高架点源高斯扩散模型，这时的排放浓度为C2=406.92 mg·m-3、排放速度为V2=1 200 m3·h-1、在下风距离X=51 000 m、污染源的有效高度为H=H0+Δh2，将数据代入公式(2)可求解出中午12时下风向点浓度函数，形式见上。晚上21时属于下午16时至晚上21时这段期间，符合瞬时高架点源高斯扩散模型，求解过程同早上8时。

最后，将求得数据转化为AQI，对照空气质量指标判断空气质量等级。

2.3 连续高架线源高斯扩散模型

2.3.1 研究思路

多污染源是指n个点污染源n→∞在时的情况，此时可将无穷多个密集的点看成连续状态下的污染发生源，即从点到线，构造线源排放模型[5]。并利用此模型对北京环城高速的汽车污染排放情况进行评判，作出时序图分析空气污染浓度梯度变化，并利用PAQI评判空气质量等级，最后基于谨慎性原则再利用AQI二次评判。

2.3.2 模型的构建

假设气象条件恒定不变且风向水平。污染气体沿X轴向横侧和垂直方向自由扩散，假设Y轴、Z轴上浓度分布服从二维正态分布。假设相对于观测点，高速公路平直且无限长，则利用积分可得高斯线源排放模型。并利用模型，综合统计数据，求解分析2015年1月16日北京二环、四环(5km)六环路(20km)早上8时、中午12时、晚上21时空气污染浓度梯度变化及空气质量等级。

利用点源的空气扩散高斯模型，对Y积分得到无限长连续线源高斯模型[6]数学表达式：

再考虑风向，则可解得地面浓度：

其中ρ为任意一点污染物的浓度，q(kg·h-1)为排放量，H为有效源高H=Hs+ΔH,Hs为几何高度，ΔH为烟羽抬升高度，β为风向与线源的夹角。

3 北京市空气状况分析

3.1 问题的简化

由于高速公路相对于观测点为无限长，不存在线源末端，故选择采用用无限长连续线源高斯模型求解汽车尾气排放污染浓度。

首先，基于求解需要，对北京二环、四环、六环图形进行简化如下(见图1)：

图1 北京二、四、六环城高速公路(从下向上)简化图

收集北京市2015年1月13日至1月16日的天气情况整理如下(见表4)：

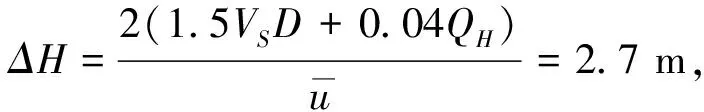
3.2 问题求解

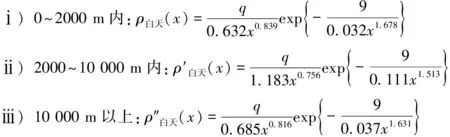
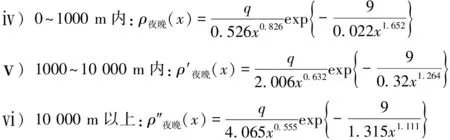
3.2.1 不考虑公路之间的相互影响

当在环城高速上测量的时候，可将与污染物的距离视为0，构造极限如下所示：

对原初式运用洛必达法则求极限值，由于分子分母均为初等函数，排放量q与x无关，所以，其极限存在。令

3.2.2 考虑公路之间的相互影响

先假下风向对上风向的影响忽略不计。考虑各公路之间的影响，需要引入各环城高速之间的距离。通过查阅文献资料得知，北京市第二环城高速与第四、第六环城高速的平均水平距离为6km与21km。依照距离以及公式组可以算出公路之间污染物扩散的影响浓度。

二环对四环的影响(6km)，用公式ⅱ、ⅴ，即

令其中的常数项

综合自身污染状况与其它路径干扰，得到北二环、四环、六环的污染浓度表达式如下：

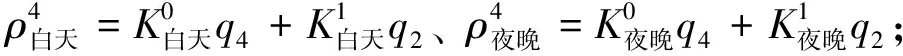
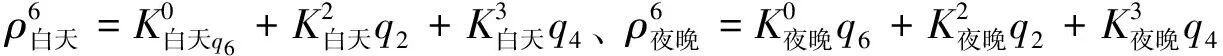
由于汽车是北京市氮氧化物的主要排放者，所以直接用氮氧化物的指标来计量空气质量等级，也就是这里的排污量q。并用氮氧化物排放的指标变化来反映北京市空气污染浓度梯度。

通过查找相关文献，了解到每千辆汽车每天排出一氧化碳约3 000kg,碳氢化合物200～400kg,氮氧化合物50～150kg[7]。调查得北京市二四六环限行前后车流量情况(见表5)。

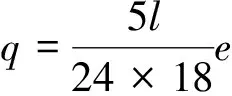
表5 北京市二四六环车流量(千辆每小时)

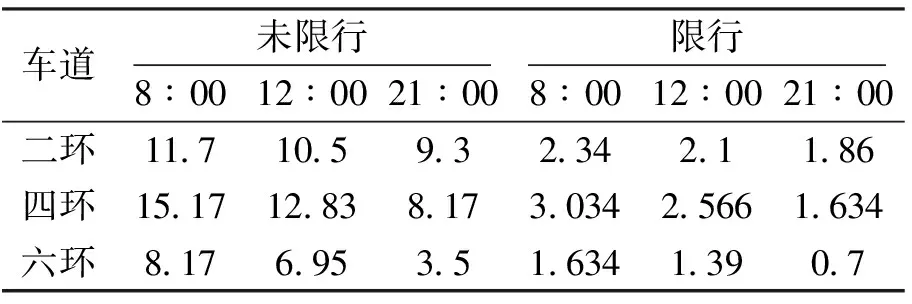
表6 北京市二四六环q值

表7 未限行北京市二四六环ρ值

表8 限行后北京市二四六环ρ值

将此值与国家标准比较即可得到空气质量指数，继而通过分级表查询得到空气质量等级。

将参数视为常参数，考察北京市二四六环限行前后ρ值表与部分数据，可得到：从时序上看，浓度从8时到21时顺次递减；从空间上看，四环的污染物浓度最高，其次是二环，最末是六环。限行前后比对，所有路线污染物浓度均显著下降，该政策效果显著[9]。

4 结 论

在建模过程中充分考虑各模型的可行性与合理性，通过对模型的求解结果分析得知影响空气质量的关键参数指标有：风速、大气情况、污染源模式、污染源排污状态(排放浓度与排放速度)、地面是否有障碍物等。空气质量的优良与生活息息相关，治理京津冀地区的空气污染迫在眉睫。

[1]第十二届数学建模五一联赛B题[EB/OL].http://www.saikr.com/wuyi/2/1427.html.2015-05-01.

[2]GB/T3840-91.制定地方大气污染物排放标准的技术方法[S].

[3]刘克强.烟羽抬升估算和观测方法[J].辐射防护通讯,1986,(02):47-49.

[4]邹本东,徐子优.因子分析法解析北京市大气颗粒物PM10的来源[J].中国环境监测，2007,23(02):79-85.

[5]孙庆珍,董晓马,任忠斌.大气点源扩散模型的GIS可视化研究[J].测绘科学,2011,36(02):24-26.

[6]王寒梅,贾秩然.大气污染物扩散模型应用研究[J].辽宁师专学报,2006,8(02):78-79.

[7]王文,于雷.基于高斯线源模式的主要尾气扩散模型综述[J].交通环保,2004,25(05):7-10.

[8]李晓童,夏明月,林善冬.基于Bootstrap方法对北京空气质量回归分析[J].河北北方学院学报：自然科学版，2014,30(04):1673-1492.

[9]李玉敏,李明丽,焦智康.北京市空气质量影响因素计量经济分析[J].中国城市经济,2011,29(09):260-261.

[责任编辑：王荣荣 英文编辑：刘彦哲]

Air Pollution Study in Beijing-Tianjin-Hebei Region Based on Gaussian Model

ZHANG De-xin,CHEN Chun,ZHU Han,YU Tian

(Institute of Statistics and Applied Mathematics,Anhui University of Finance and Economics,Bengbu,Anhui 233030,China)

Objective In view of the air quality index and the pollution sources in Beijing-Tianjin-Hebei region,a new standard of air quality was set up to define the level of air on the basis of national standard(AQI).Methods A reasonable model was established to study the spread type of the pollutes.By using fuzzyC-means clustering,fuzzy comprehensive evaluation,F-test,and classification discussion,the paper built air quality measurement system,continuous overhead Gaussian diffusion,instantaneous elevated point source Gaussian diffusion,and continuous line source Gaussian diffusion model.By using MATLAB,the SPSS software,the key parameters affecting the quality of the air were obtained.According to a thought from divergency to continuation and by using integral,a line source Gaussian diffusion model was established.The NationalAmbientAirQualityStandardwas used to determine vertical diffusion parameters,and then to analyze the air pollution concentration of Beijing Second ring,Fourth-ring and Sixth-ring.Results The result showed that the Fourth-ring had the highest pollutant concentrations,followed by the Second-ring,and the bottom was the Sixth-ring,diminishing concentration from 8∶00 to 21∶00.When comparing data before and after restriction,all routes pollutant concentration decreased significantly.The effect of restriction policy was remarkable.Conclusion The main causes of pollution in Beijing-Tianjin-Hebei region were the use of motor vehicles,industrial emissions and the burning of fossil fuels such as coal and oil,etc.The suggestion was given to control air pollution in the Beijing-Tianjin-Hebei region.

Gaussian model;air pollution;fuzzy clustering;comprehensive evaluation;F-test

国家自然科学基金项目(11301001);国家级大学生创新项目(201510378020)；安徽财经大学教研项目(acjyzd201429)

张德鑫(1994-),女，安徽滁州人，安徽财经大学统计与应用数学学院在读学生，研究方向：数学与应用数学。

陈春(1981-)，女，安徽泗县人，安徽财经大学统计与应用数学学院讲师，硕士，研究方向：应用数学。

X 51

A

10.3969/j.issn.1673-1492.2017.01.008

来稿日期：2016.05.11