一种敏捷卫星积分时间计算方法

朱剑冰，张猛，汪路元，袁珺，程博文，赵魏

北京空间飞行器总体设计部，北京 100094

一种敏捷卫星积分时间计算方法

朱剑冰*，张猛，汪路元，袁珺，程博文，赵魏

北京空间飞行器总体设计部，北京 100094

敏捷卫星成像过程中姿态变化灵活，积分时间变化剧烈，传统卫星积分时间计算模型已无法满足精度要求。因此，提出一种改进的积分时间计算模型，在星地斜距计算和摄影点地速计算两方面作了改进。星地斜距计算时利用地表数字高程模型修正理论的斜距值，摄影点地速计算中增加姿态角速度对卫星本体坐标系角速度矢量的影响，并设计了整个算法在星上数管分系统中的实现方案。最后在星载嵌入式环境下进行了仿真计算，并与地面仿真计算结果进行了比对分析。两者比对偏差在0.01‰以内，可以满足相机成像质量要求。

敏捷卫星；积分时间；速高比；数字高程模型；数管分系统

时间延迟积分电荷耦合器件(Time Delay and Integration Charge Coupled Device，TDICCD)具有高光电灵敏度和信噪比，因此目前新型敏捷卫星通常采用TDICCD线阵推扫成像1-3]。TDICCD成像需要光生电荷包的转移与像面图像的运动保持同步4]，即积分时间内相机焦面上的像移应与相机单个像元的长度相同。如果积分时间计算不准确，会导致像移模糊，调制传递函数(Modulation Transfer Function，MTF)下降3,5-6]。传统的遥感卫星对地成像时仅有滚动方向的侧摆(被动推扫成像)7]，成像过程中积分时间变化很小，积分时间的计算非常成熟，工程实现相对简单。敏捷卫星除了支持传统卫星的被动推扫成像外，还支持主动推扫、非沿迹推扫8]等复杂成像模式。敏捷卫星成像过程姿态变化灵活，三轴方向都可以变化，并且三轴姿态角速度都可以不为零9]。卫星在进行“动中成像”时，光轴斜距的剧烈变化不仅带来图像比例尺的改变，而且会造成相机像面图像运动角速度的变化，进而引起相机积分时间参数在成像过程中的剧烈变化10]。

文献11]给出了一种积分时间计算关键过程速高比(速高比乘以常量系数即为积分时间)计算的数学模型，该方法主要针对传统卫星被动推扫成像，没有考虑地表数字高程对斜距的影响和敏捷成像时卫星三轴姿态角速度对地速影响，因此本文在分析敏捷卫星与传统卫星差异的基础上，对文献12]中的速高比计算模型进行了改进，提出一种敏捷模式下积分时间计算方法，将该方法在星上数管分系统中进行了仿真实现，并将实现的结果与美国卫星工具包(Satellite Tool Kit，STK)13]的仿真计算的结果进行了比对分析，分析结果表明本文方法的有效性，该方法可以广泛应用到中国后续敏捷卫星中。

1 敏捷卫星积分时间计算方法分析

1.1 积分时间计算的基本原理

积分时间定义为相机像元尺寸与像速的比值。如图1所示。

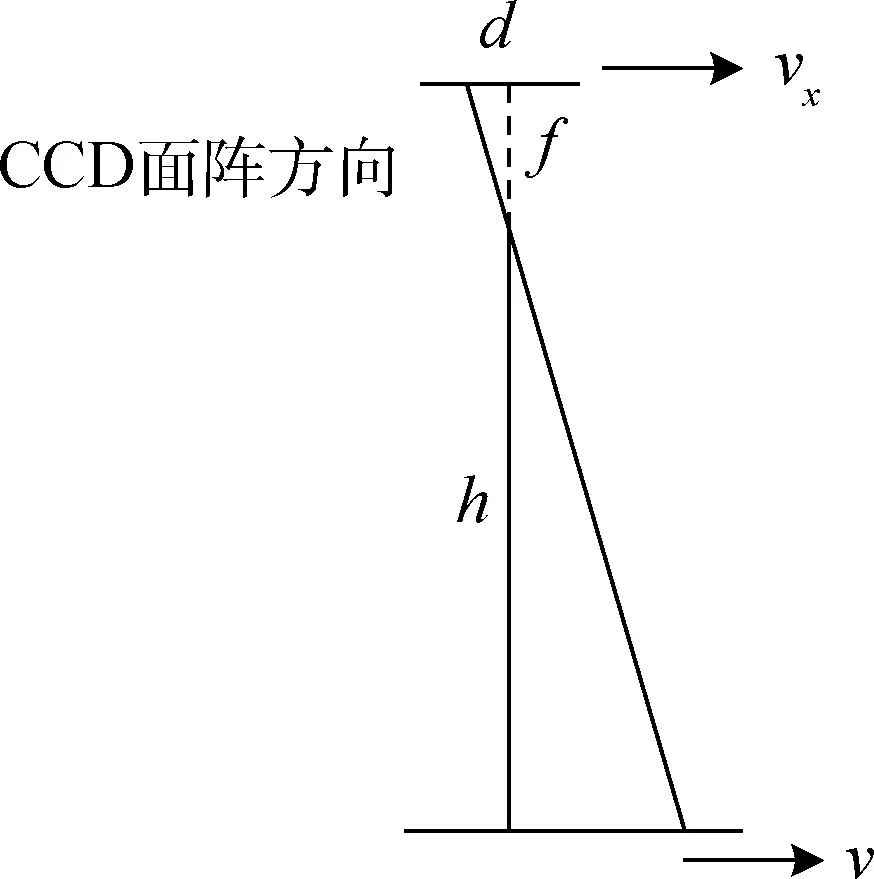
图1 积分时间计算示意Fig.1 Calculation sketch of integral time

积分时间计算公式如下：

(1)

式中：vx为地面景物在相机焦平面上的运动速度；f为相机的焦距；d为像元尺寸；v为摄影点地速。d和f对于固定的相机都是已知量，因此积分时间计算的核心是求出斜距h与摄影点地速v的比值(简称速高比)。

1.2 速高比模型改进

敏捷卫星相比传统卫星，姿态灵活性更强，成像过程三轴姿态角速度可以不为零，导致摄影点地速可以实时变化，因此计算摄影点地速时需考虑姿态角速度带来的影响。同时星地斜距的计算要求精度更高，不能采用文献11]斜距的粗略计算模型，需要利用光轴矢量和地球交点的精确模型，同时需考虑数字高程对斜距的影响。因此利用传统卫星积分时间计算模型获得的积分时间精度无法满足敏捷卫星成像质量要求，因此本文算法对斜距计算模型和摄影点地速计算模型进行了改进。

(1)斜距模型的改进

文献11]斜距的计算模型为粗精度模型，实际计算过程中需利用地面数字高程对斜距进行修正，获得更精准的斜距值，从而保证积分时间计算的精准性。计算模型如图2所示。

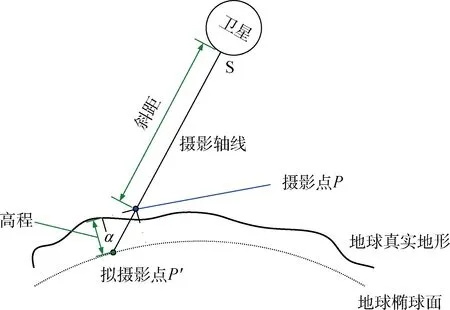
图2 斜距计算模型示意Fig.2 Calculation model sketch of height

在惯性系中，求出与旋转椭球面相交的拟摄影点P′后，通过该点建立相对旋转椭球面的切平面，该切平面的法矢量n为：

(2)

摄影线SP'在P的切平面内的仰角与SP和n的夹角α互补：

(3)

式中：HPS表示摄影点P到卫星S的距离矢量。

在惯性系中，将拟摄影点P′的坐标转换到地固系中，通过数字高程模型查出当前的高程Δh，根据坐标的平移和旋转不改变矢量长度的特性，对摄影点斜距进行修正：

(4)

(2)摄影点地速模型的改进

在传统卫星积分时间计算过程中认为本体坐标系具有的角速度矢量与卫星的轨道角速度矢量相等。但敏捷卫星需考虑姿态角速度，本体坐标系角速度矢量：

(5)

式中：ωb为本体坐标系具有的角速度矢量；ωn为卫星的轨道角速度矢量；ωs为卫星姿态角速度矢量。

因此考虑姿态角速度，敏捷模式下摄影点地速的计算公式与文献11]中的公式(13)有所区别，具体：

(6)

式中：ωe为地球角速度矢量；R为地心到目标点的矢量；r为地心指向卫星的矢径；H为卫星到目标点的距离矢量；vr是卫星绝对速度的径向分量。

2 积分时间计算在数管分系统中的 实现方案

敏捷卫星成像过程中积分时间变化剧烈，为保证积分时间更新及时性，要求在最短姿态控制周期内完成积分时间计算。目前控制分系统最短姿态控制周期为125ms，因此要求数管分系统125ms内完成一次相机积分时间计算，通常一台TDICCD相机又由多片CCD组成，每片CCD的视轴矢量与卫星本体系的三轴夹角都不相同，因此每片CCD都需单独计算积分时间。所以数管分系统需要在125ms内完成多片CCD的积分时间计算，并将计算结果发送给相机分系统。

图3为积分时间计算实现方案的数据流。数管分系统任务规划模块接收测控分系统发来的成像任务序列，对下一圈成像任务进行任务规划，根据规划结果定时将最近一次成像任务的成像时段(包括开始成像时间和结束成像时间)发送给导航子系统，控制分系统和积分时间计算模块。由于数据在1553B总线传输存在延迟并且星载计算机计算积分时间也耗费一定的机时，因此积分时间实时计算模式设计为近实时模式而非绝对实时。目前数管分系统方案中积分时间计算的输入数据都是未来3s后的轨道和姿态数据，计算结果也是未来3s后的积分时间，这样设计可以确保相机收到的积分时间没有过时，相机可以根据积分时间数据包中的时标在指定时间设置积分时间参数，有效保证相机参数设置的及时性和准确性。导航子系统在成像时段期间外推未来3s后的轨道六根数发送给积分时间计算模块，为了降低总线通信量，轨道数据每秒仅发一组，由数管分系统负责插值获得125ms一组的轨道数。控制分系统则在成像时段期间根据成像位置规划未来3s后的姿态数据，同时为了降低总线通信频次，控制分系统与数管分系统1s交互一次，每次控制分系统将1s的姿态数据打成一个数据包(包含8组数据，125ms一组)发送给积分时间计算模块。积分时间计算模块根据任务规划模块发来的成像时段启动和关闭计算功能，这样可以有效节省星上计算资源，同时确保非成像时段相机不会收到无效的积分时间值。

积分时间计算模块主要包括以下几部分：

1)轨道数据接收与处理。数管分系统接收1553B总线上的轨道数据包，提取出轨道六根数，根据之前3s内的轨道数据按照拉格朗日二阶插值方法得到125ms一个点的轨道六根数。并按照时间顺序将这些轨道数据排入队列，供积分时间计算模块使用。

2)姿态数据接收与处理。数管分系统接收1553B总线上的姿态数据包，解包后提取所有组的姿态角和姿态角速度信息，并按照时间顺序将这些数据排入姿态数据队列，供积分时间计算模块使用。

3)相机参数获取。数管分系统RAM区需要提前固化相机积分时间计算相关的参数数据，包括相机焦距、像元尺寸、各片探测器的中心位置(相对于相机坐标系)，积分时间计算时需要读取这些参数数据，供积分时间计算模块使用。

4)数字高程模型(DEM)。DEM将全球地表高度进行网格化，每个网格点存储该区域的地表高度值，其水平坐标以WGS84为参考，垂直坐标以平均海平面为起始高程。考虑到星上存储资源限制和积分时间精度要求，本文采用0.1°×0.1°的全球DEM，并将该数据存储在Flash中，供积分时间计算模块使用，用于修正星地斜距。

5)积分时间计算。积分时间计算模块基于轨道数据、姿态数据、相机参数数据以及数字高程数据，根据本文第2节改进的积分时间计算方法，完成焦面各个探测器的积分时间计算。每125ms计算N片CCD的积分时间，并将积分时间打包发送给相机分系统，由相机分系统完成积分时间设置。每个积分时间包中由1个时标和N个积分时间代码组成(对应于N片CCD)。

3 计算结果分析

3.1 仿真输入条件

(1)轨道参数。

历元：2015年7月1日12：00：00(UTCG)。半长轴：6 870 805.248 349 m。偏心率：0.000 483。轨道倾角：97.356 591°。升交点赤经：256.526°。近地点幅角：0.0°。平近点角:360.0°。

(2)仿真时间

2015年7月1日12：00：00(UTCG)～2015年7月1日12：08：00(UTCG)。

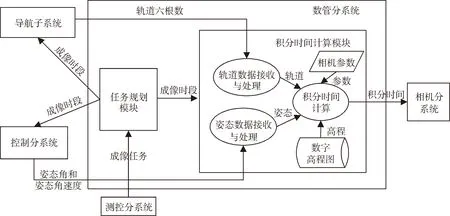
图3 实现方案的数据流Fig.3 Data flow chart of implementation

相机焦距11 m，像元尺寸10 μm。

(3)卫星运行工况

为了充分验证算法的正确性，本文选取了4种最典型的工况进行算法验证，4种工况的运行时间都为30 s。

1)工况1：恒角速度推扫模式。侧摆0°，起始俯仰角+25°，俯仰方向姿态角速度恒定-0.8(°)/s。

2)工况2：正常推扫模式。侧摆25°，俯仰25°，正常推扫无回扫。

3)工况3：正常推扫模式。侧摆25°，俯仰0°，正常推扫无回扫。

4)工况4：恒线速度推扫模式。起始点(经度1.381 356 04°，纬度6.917 281 49°)，结束点(经度1.546 718 98°，纬度7.739 859 87°)。

3.2 仿真运行的环境

(1)仿真环境软硬件配置

算法运行的嵌入式环境如表1所示。

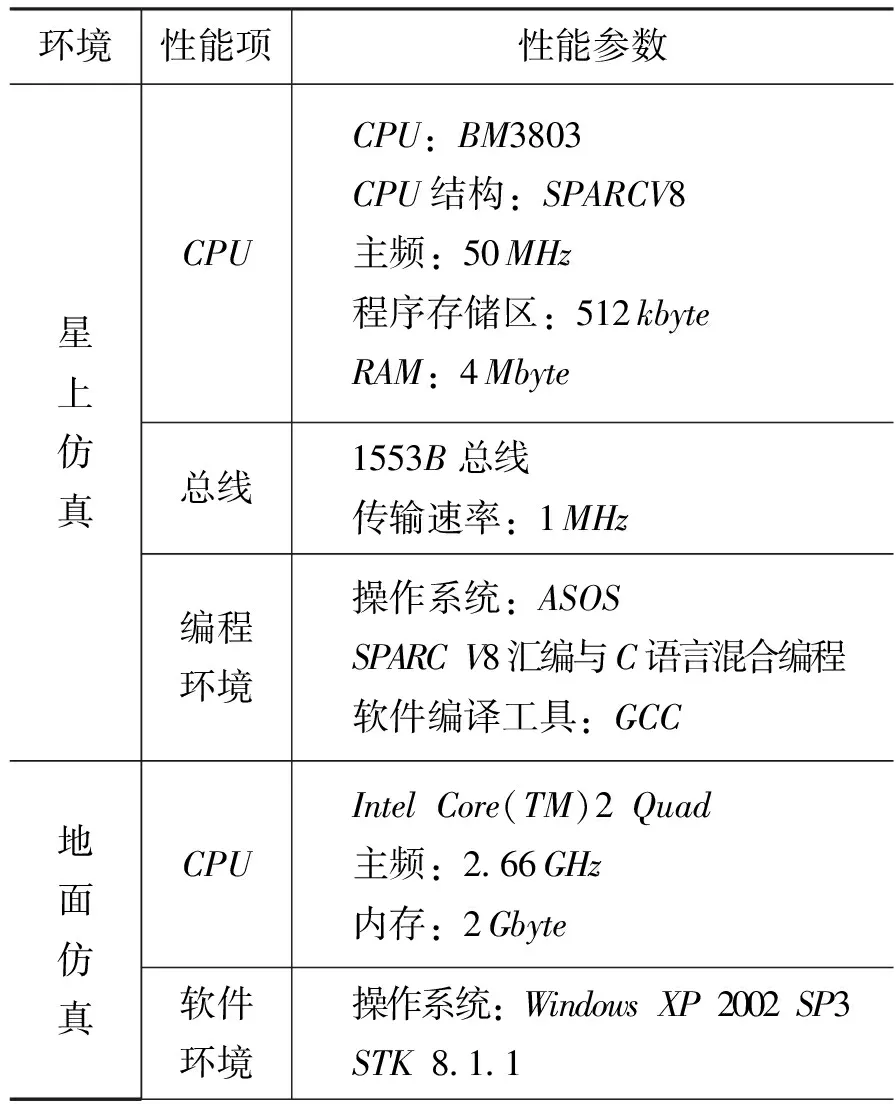
表1 仿真环境

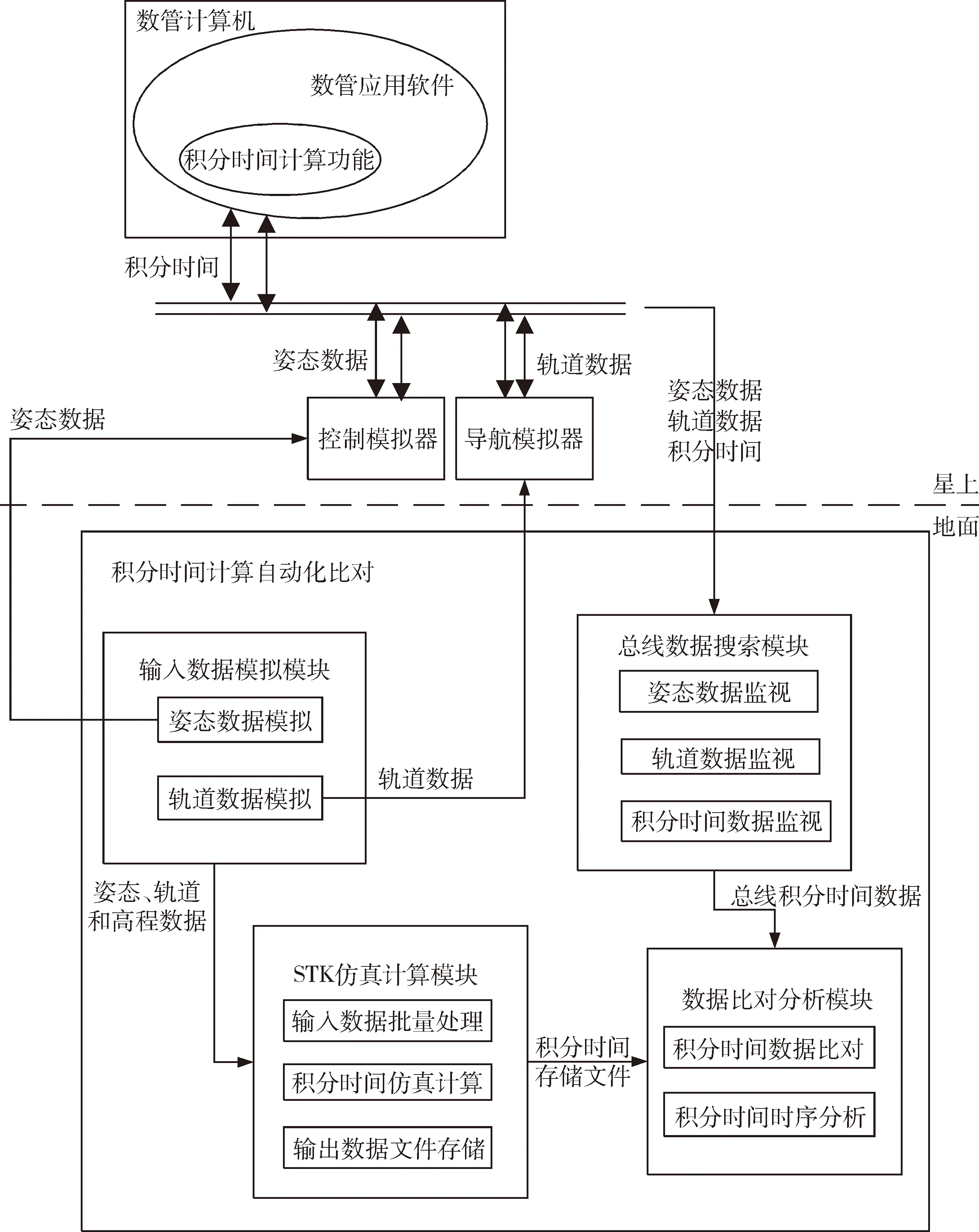
图4 仿真测试平台Fig.4 Experiment testing platform

(2)仿真测试平台

由于积分时间计算过程中涉及姿态和轨道数据模拟生成及数据在1553B总线上的动态传输，测试过程较为复杂，因此专门开发了一套积分时间仿真测试平台，如图4所示。

该平台中输入数据模拟模块主要完成姿态、轨道等输入数据的模拟，总线数据搜索模块完成对总线数据的查询分析，为数据比对分析提供数据支持。STK仿真计算模块利用STK模型完成积分时间计算，数据比对分析模块完成星上计算结果与地面结果的比对分析。星上数管计算机按照本文算法完成实时积分时间计算。

3.3 仿真结果分析

将本文的算法在星载嵌入式环境下进行仿真运行，运行结果与STK仿真计算结果进行差值比对。两种工况下的差值比对结果如图5所示。可以看出本文算法得到的积分时间与STK仿真计算的结果非常接近，比对偏差在0.01‰之内，可以满足相机成像质量要求。

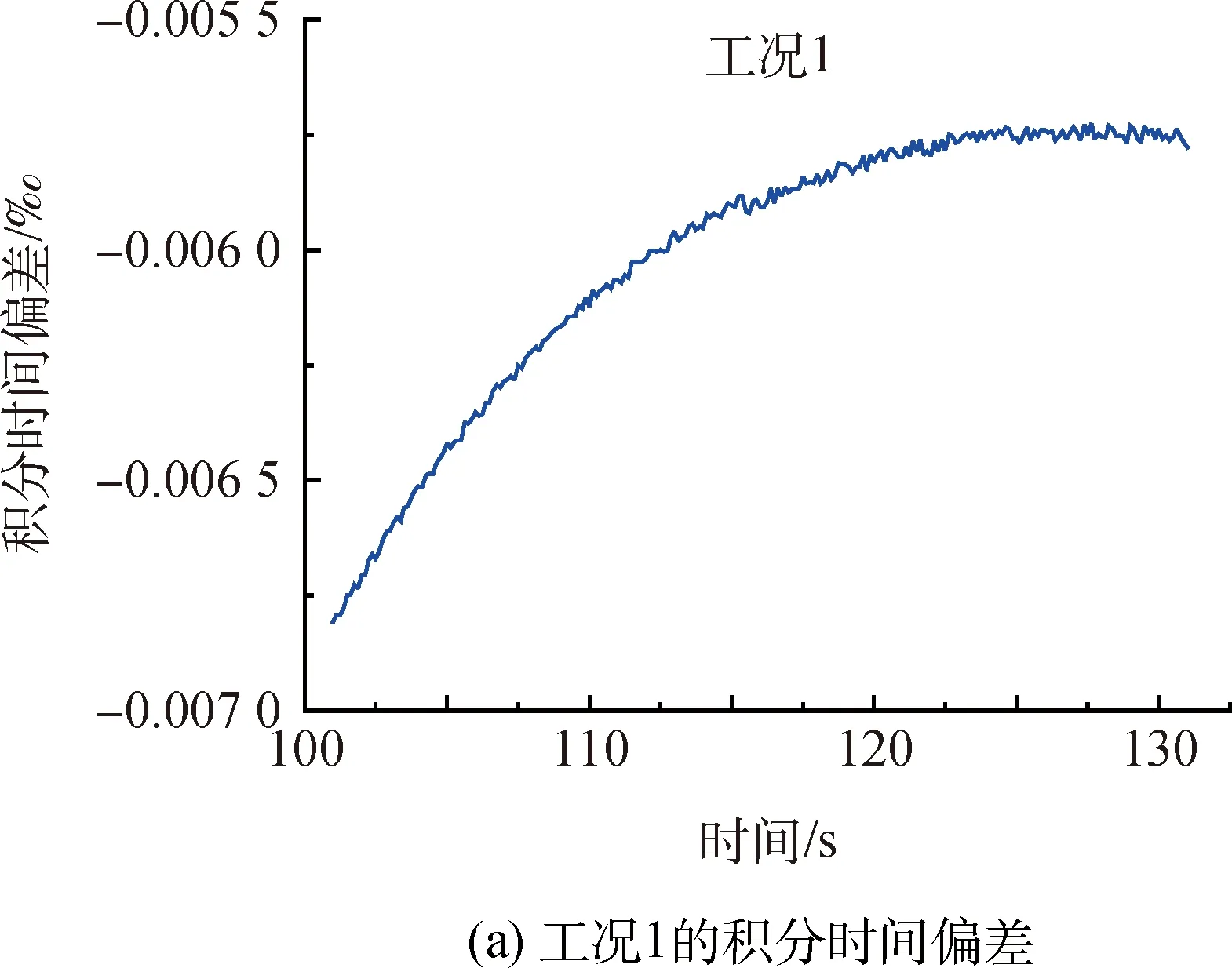
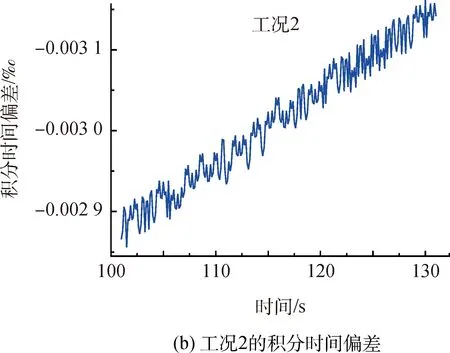
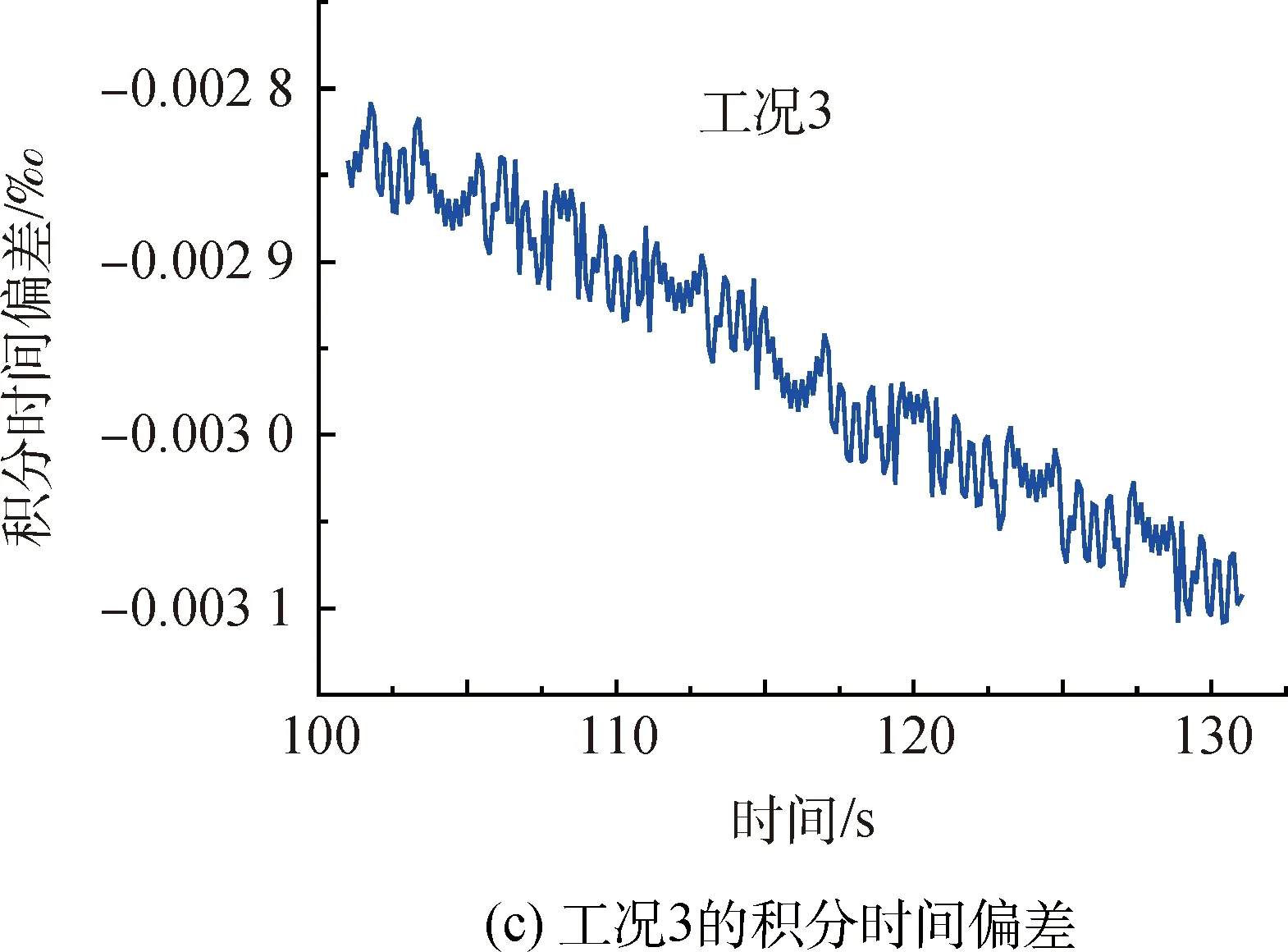
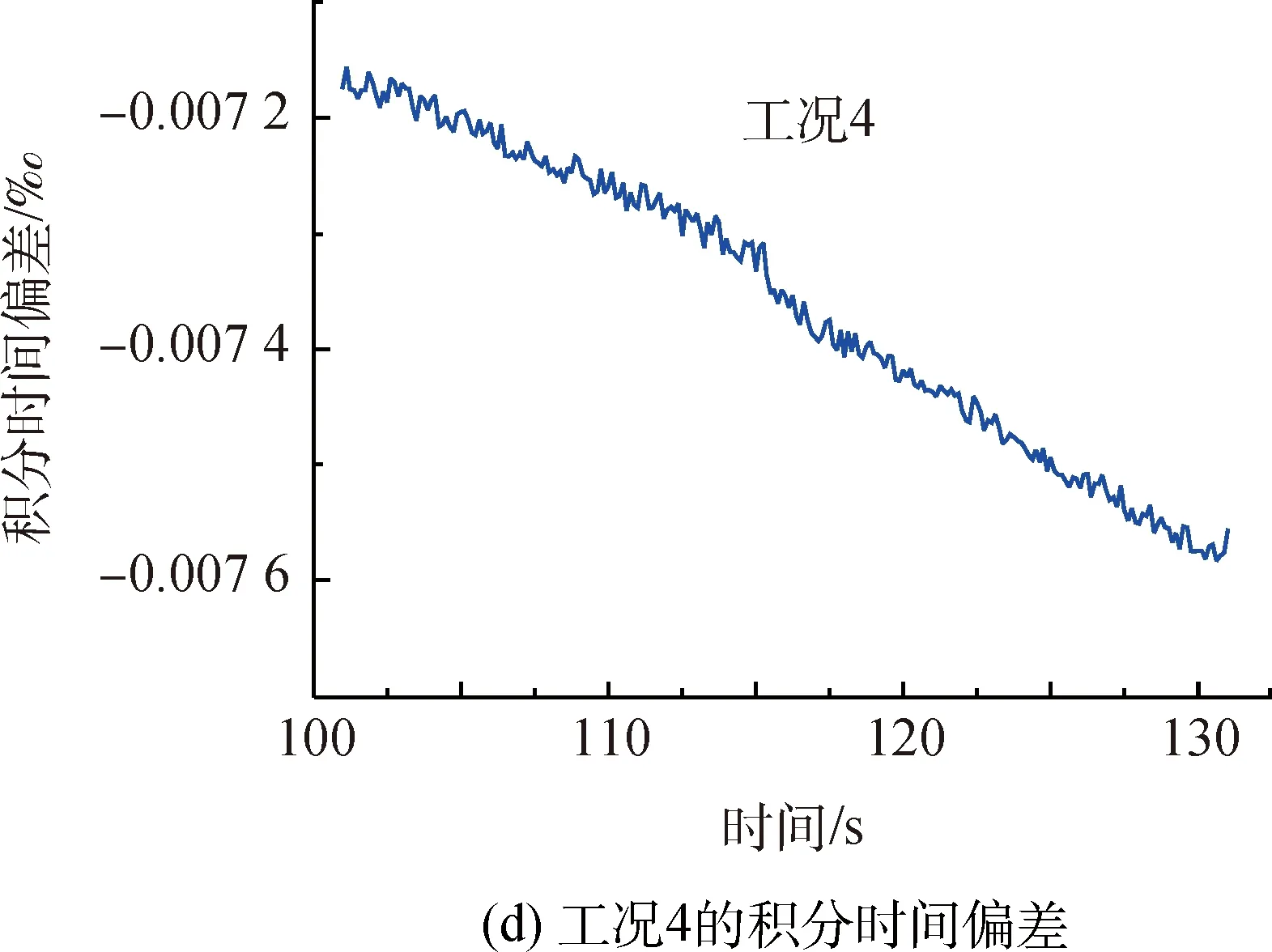
图5 仿真结果Fig.5 Experiment results

4 结束语

针对敏捷卫星姿态变化灵活，积分时间变化剧烈的特点，本文从摄影点地速计算和斜距计算两方面改进了传统积分时间计算模型，并通过试验验证了本文方法有效可行，但算法在实际嵌入式环境运行过程中仍然占用较大机时，导致积分时间计算时星载处理器资源非常紧张，下一步将继续研究该算法在星载嵌入式环境下的优化实现工作，为下一步算法在后续敏捷卫星型号中的应用奠定基础。

References)

[1] 彭成荣. 航天器总体设计M].2版. 北京：中国科学技术出版社，2011：353-354.

PENG C R. System design for spacecraftM]. 2nd ed. Beijing：China Science and Technology Press，2011：353-354.

[2] 孙俊,赵鸿志，杨芳. 敏捷卫星立体定位角元素影响分析J]. 中国空间科学技术，2014，34(6)：72-78.

SUN J，ZHAO H Z，YANG F. Analysis on attitude angle impacting stereo positioning accuracy for agility satelliteJ]. Chinese Space Science and Technology，2014，34(6)：72-78(in Chinese).

[3] 张林，吴晓琴，袁暋. TDI-CCD相机动态成像的速度同步控制研究J]. 传感器技术，2005，24(12)：10-12.

ZHANG L，WU X Q，YUAN M. Synchronous control research of TDI-CCD camera dynamic imagingJ].Journal of Transducer Technology，2005，24(12)：10-12(in Chinese).

[4] 刘光林，杨世洪，吴钦章. 一种基于CCD多电极结构的电子像移补偿方法J].光电子激光，2008，19(7)：947-948.

LIU G L，YANG S H，WU Q Z. An image motion compensation method based on multiphase CCDJ]. Journal of Optoelectronics Laser，2008，19(7)：947-948(in Chinese).

[5] 樊超，李英才，易红伟. 速高比对TDICCD相机的影响分析J].兵工学报，2007，28(7)：817-818.

FAN C，LI Y C，YI H W. Influence of velocity-height ratio of satellite on the TDICCD cameraJ]. Acta Armamentarii，2007，28(7)：817-818(in Chinese).

[6] 郭永飞. 侧摆成像下多片TDICCD拼接相机分段异速研究J].光机电信息，2010，27(10)：33-34.

GUO Y F. Research on subsection image motion mismatching for multi-TDICCD mosaic camera of scroll imagingJ]. OME Information，2010，27(10)：33-34(in Chinese).

[7] 孙凯，白国庆，陈英武.面向动作序列的敏捷卫星任务规划问题J]. 国防科技大学学报，2012，34(6)：141-142.

SUN K，BAI G Q，CHEN Y W. Action planning for agile earth-observing satellite mission planning problemJ]. Journal of National University of Defense Technology，2012，34(6)：141-142 (in Chinese).

[8] 张新伟，戴君，刘付强. 敏捷遥感卫星工作模式研究J]. 航天器工程，2011，20(4)：33-35.

ZHANG X W，DAI J ，LIU F Q. Research on working mode of remote sensing satellite with agile attitude controlJ]. Spacecraft Engineering，2011，20(4)：33-35(in Chinese).

[9] 黄群东，杨芳，赵键. 姿态对地指向不断变化成像时的偏流角分析J]. 宇航学报，2012，33(10)：1544-1551

HUANG Q D，YANG F，ZHAO J. Drift angle analysis for agile satellite imaging when its attitude points to earth changing continuouslyJ]. Journal of Astronautics，2012，33(10)：1544-1551(in Chinese).

[10] ZHANG X W，DAI J，LIU F Q. Research on working mode of remote sensing satellite with agile attitude controlJ]. Spacecraft Engineering，2011，20(4)：1545-1546(in Chinese).

[11] 周虎，王小勇. 积分时间不同步对TDICCD空间探测相机成像质量影响的仿真C]. 2010年第二十三届全国空间探测学术交流会，厦门，中国空间科学学会，2010.

ZHOU H，WANG X Y. Simulation on influence to image quality of space CCD camera based on integral time not synchronizationC]. 2010，the 23th National Conference on Space Exploration Technology in China， Xiamen，CSSR(in Chinese).

[12] 陈绍龙. 侧摆摄影偏流角和速高比的计算模型J].航天器工程,2010，19(1)：37-39.

CHEN S L. Computation model of veer angle and velocity-height ratio for space camera in roll attitudeJ]. Spacecraft Engineering，2010，19(1)：37-39(in Chinese).

[13] 杨颖，王琦. STK在计算机仿真中的应用M]. 北京：国防工业出版社，2005：82-86.

YANG Y，WANG Q. Computer simulation based on STKM]. Beijing：Defense Industry Press，2004：82-86(in Chinese).

(编辑：车晓玲)

An integral time calculation method for agile satellite

ZHU Jianbing*，ZHANG Meng，WANG Luyuan，YUAN Jun，CHENG Bowen，ZHAO Wei

BeijingInstituteofSpacecraftSystemEngineering，Beijing100094，China

Traditional integral time calculation models can′t satisfy the accuracy requirement, because attitude flexibility and integral time change severely during the imaging of agile satellite. An integral time calculation model was proposed to improve the aspects of ground velocity calculation of imaging point and height calculation from satellite to ground point. Digital elevation model was adopted to correct height value for height calculation from satellite to ground point. And the attitude angular velocity′s impact to angular velocity vector in the satellite body coordinate system was considered when calculated the ground velocity at imaging points. The whole algorithm implementation on OBDH subsystem was designed and simulation calculation under the embedded environment was conducted. The analysis results manifests the method can meet the accuracy requirement of agile satellite camera imaging quality since the difference is within 0.01‰ by comparison with STK simulation calculation results.

agile satellite；integral time；velocity-height ratio；digital elevation model(DEM)；OBDH subsystem

10.16708/j.cnki.1000-758X.2017.0018

2016-05-10；

2016-10-25；录用日期：2016-11-24；

时间：2017-02-16 18:39:39

http:∥www.cnki.net/kcms/detail/11.1859.V.20170216.1839.010.html

朱剑冰(1984-)，男，硕士，高级工程师，xgdzjb@163.com，研究方向为星载自主任务规划技术

朱剑冰，张猛，汪路元，等. 一种敏捷卫星积分时间计算方法J].中国空间科学技术,2017,37(1)：97-103.ZHUJB，ZHANGM，WANGLY,etal.AnintegraltimecalculationmethodforagilesatelliteJ].ChineseSpaceScienceandTechnology, 2017,37(1)：97-103(inChinese).

TN216

A

http:∥zgkj.cast.cn