显示多体动力学方程自动编制技术

李瑾岳，胡权，张景瑞

北京理工大学 宇航学院，北京 100081

显示多体动力学方程自动编制技术

李瑾岳，胡权*，张景瑞

北京理工大学 宇航学院，北京 100081

为高效得到复杂柔性多体航天器的动力学方程解析表达式，研究了系统动力学方程自动编制技术。首先，基于Kane方法推导了构型简单的链状多体系统动力学显式方程；然后，根据方程中各项物理意义和分布规律，开发了适用于树状构型多体航天器的解析动力学方程输出程序，并运用Latex软件对输出文本进行二次编译，增强输出复杂数学公式的可读性。所得方法极大地简化了对此类航天器的建模工作。

多柔体系统；机械臂；显式动力学方程；自动编写；Kane方程

随着航天任务的复杂化，航天器多为由多个部件组成的多体系统。建立此类系统的动力学方程成为系统特性分析和控制设计的前提。Hooker和Margulies首先将多体动力学的概念运用于航天器系统建模1]，基于牛顿/欧拉法推导了任意数量刚体组成的树形多体系统动力学方程，但涉及的约束力消元成为该方法的难点。之后，Hooker使用拉格朗日方法避免方程中出现未知约束力2]，但拉格朗日法分析系统计算量大，得到的方程形式复杂，不易于分析。同一时期，达郎贝尔原理、汉密尔顿方法、波兹曼/海默方法等其他方法也都曾被用于系统分析3]。1960年起，Kane发表了系列论文4-6]，提出基于新的运动学变量——偏速度，简化了方程的推导，仅需要将偏速度与已知向量(惯性力、惯性力矩、接触力、接触力矩)点乘，即可得到系统的运动方程。

以上方法可用于数值推导或符号推导系统动力学方程。对系统运动的解算，依赖方程的数值计算与求解；但是，若能获得系统显式的动力学方程，则能够对系统特性分析提供模型参考。早期对于计算机符号分析法应用的尝试未能取得成功，这是由于在对方程进行计算时，出现了大量的中间表达数，致使计算机内存不足7]。随着Kane方法的运用，这一问题得到了解决。Levinson首先展示了Kane算法与符号分析法结合的可行性8]；几乎同时，Schiehlen和Kreuzer宣布了基于符号分析法及牛顿/欧拉方程研发的多体动力学代码，NEWEUL9]。不久之后Rosenthal及Sherman基于凯尔方法开发了商业软件SD/EXACT10]。近些年，另一些符号动力学程序也被开发了出来，如AUTOLEV11]和SYMKIM12]。这些基于符号分析法的代码非常适合运用于具有少量刚体的系统，但并不能很好地处理具有多个柔性体的模型。而大多数可处理具有大量柔性体系统的商业软件仍然使用数值分析法13]。

本研究基于已有的显式多体系统动力学方程，发现链状及树状多柔体系统的显式动力学方程形式上的规律，以及动力学方程形式与系统构型间的联系，提出一种显式系统动力学方程高效编写方法。此方法适用于具有树状结构的多柔体系统，并可将柔体退化为刚体。同时为了提高输出方程的可读性，基于Latex排版程序对输出文本进行了二次编辑，便于后续解析的分析各项的物理含义。最后给出了应用实例。

1 多柔体系统动力学方程的推导

以带有一部机械臂系统的空间链状多体系统为例，说明系统方程内部的固有规律。如图1所示，中心体与机械臂间、机械臂的3节臂杆之间采用铰链铰接。假定每个铰链具有1～3个相对转动自由度。

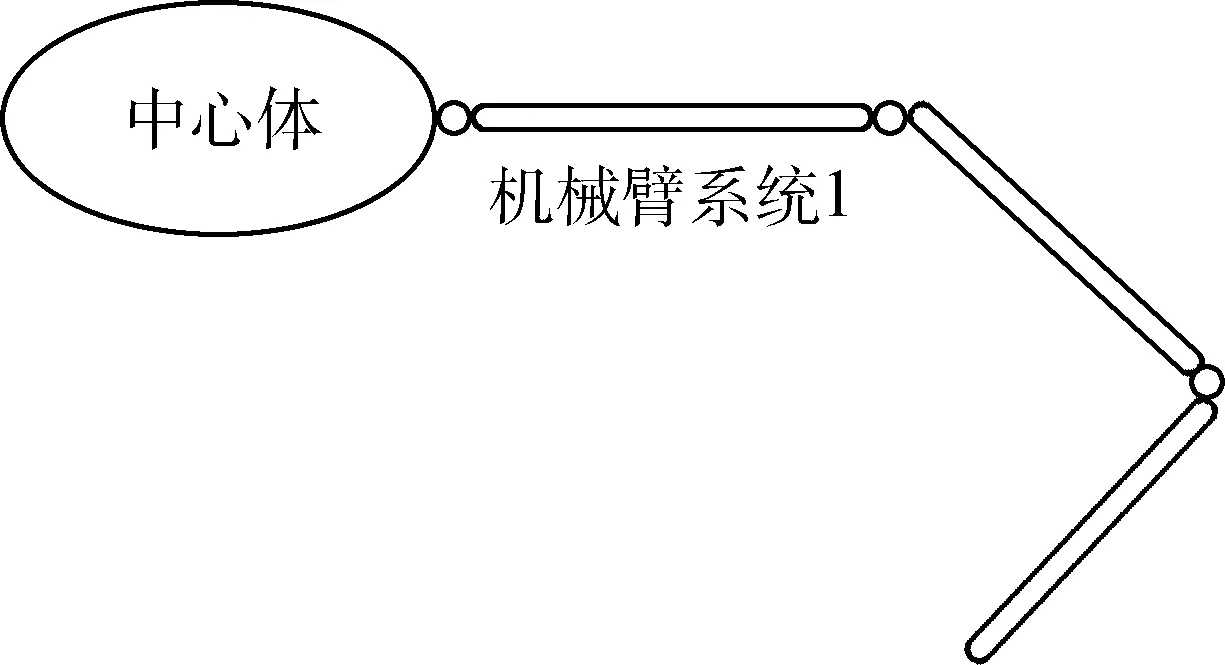
图1 目标系统的构型示意Fig.1 Structure of target system

1.1 系统的矢量定义

为方便描述系统及各臂杆运动，引入中心体体坐标系，其原点位于复杂连接体中心Ob,Xb轴、Yb轴与Zb轴为复杂连接体中心体的惯性主轴，且构成右手坐标系；机械臂臂杆坐标系，原点位于机械臂系统中第j节机械臂臂杆与其内接体的铰链Oj处，坐标系各轴与第j节臂杆固连；在本系统中，j=1,2,3。

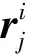
根据以上定义的位置矢量，可以得到各体质量微元在惯性系中的位置矢量14]：

(1)

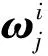
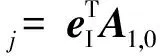
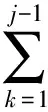
(2)

式中：Aj,k表示从单位基向量bk到bj的坐标转换矩阵。

位置矢量对时间求一阶导数，便可求得系统中各体参考质量点的速度矢量。

(3) 2)第1节臂杆质量微元：

(4)

3)第2节臂杆质量微元：

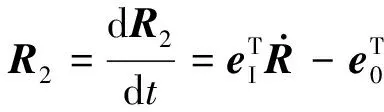
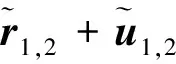
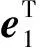
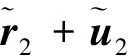
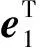
(5)

4)第3节臂杆质量微元：

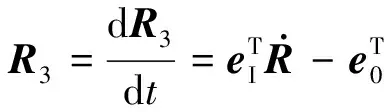
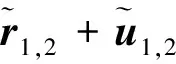
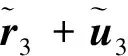
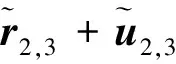
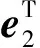
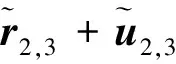
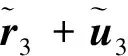
(6)

为简化后续推导，定义：

(7)

(8)

(9)

速度矢量中，uj,j+1为因弹性变形而产生的位移。

速度矢量对时间再次求导即可得加速度矢量，这里不再给出加速度矢量的具体形式。

1.2 动力学方程的推导

Kane方程15-16]的一般形式：

(10)

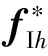
在上述广义力公式中，Gh为偏速度向量，系统广义速度表示为v，则有：

(11)

式中：Wh为选定的系统广义偏速度15]。

由式(11)可得，偏速度向量Gh可表示为速度向量v对各阶偏速度Wh求导所得向量，即：

(12)

将各体质量微元的偏速度、加速度代入Kane方程，可得各体的动力学方程。

1)中心体的平动方程：

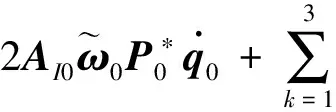
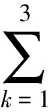
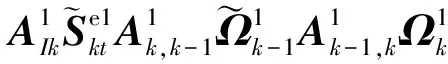
(13)

2)中心体的转动方程：

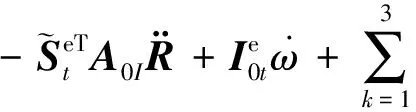
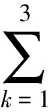
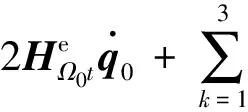
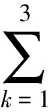
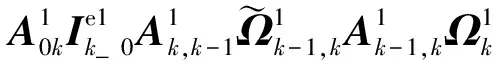
(14)

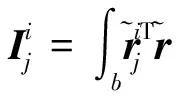
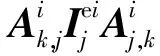
3)第k节机械臂的转动方程：

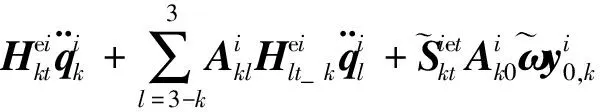
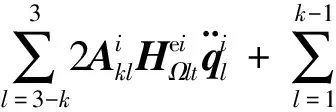
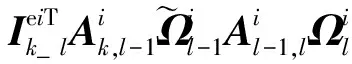
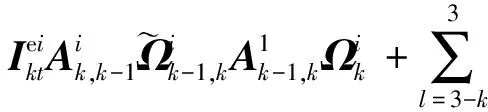
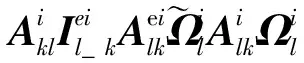
(14)

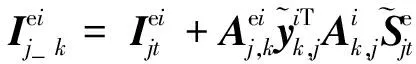
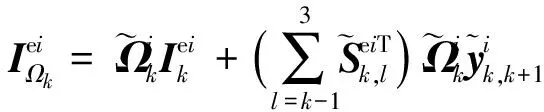
由以上各项的物理含义，可以发现显式系统动力学方程的形式与系统的构型有关，且在形式上规整，具有很强的规律性。

2 树状构型多体系统动力学方程

当系统为树状构型时，动力学方程形式会发生变化，原有显式方程形式上的规律也将随系统构型发生变化。

以图 2所示系统为例，说明方程各项的修正方法。为减小方程推导计算量，将系统退化为刚性。同上节推导思路，直接给出系统各体的显式动力学方程，并找出规律。

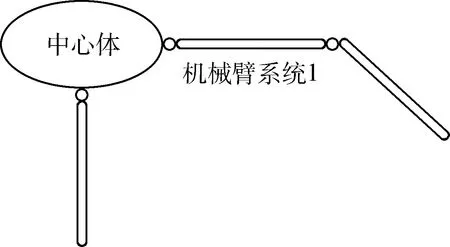
图2 存在树状构型的示例系统Fig.2 Target system with tree structure

1)中心体的平动方程：

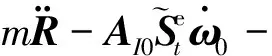
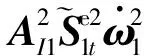
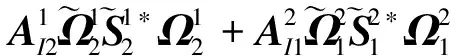
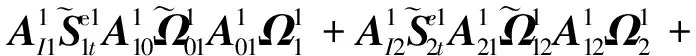
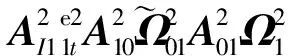
(15)

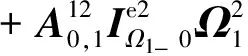
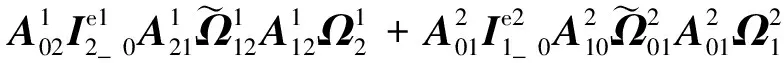
(16)

3)第1系统中第1节机械臂的转动方程：

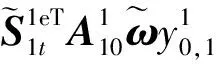
(17)

4)第1系统中第2节机械臂的转动方程：

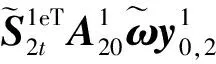
(18)

5)第2系统中第1节机械臂的转动方程：

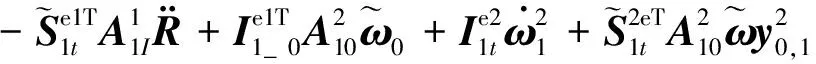
(19)

通过观察推导方程形式，得出结论：

树状构型系统显式动力学方程形式与链状构型系统显式动力学方程形式类似，方程中描述中心体运动的相关项不变，仅描述机械臂的运动的部分项发生变化，由原来描述单一机械臂运动的单一项变为描述多个机械臂运动的多个项的叠加。

3 程序框架介绍

由上节推导多体航天器系统动力学方程，发现显式动力学方程在形式上与系统构型关联，形式规整具有规律性。通过运用显式方程形式上的规律，编写了显式动力学方程自动编制程序。图3给出了程序流程。

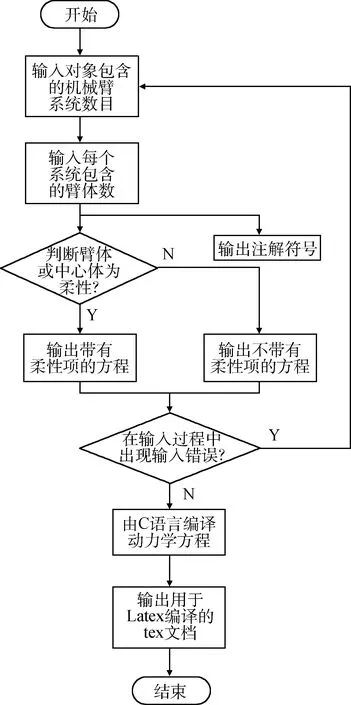
图3 程序工作流程Fig.3 Flowchart of the program

程序分为两大部分，一部分存储动力学方程的所有子项。另一部分负责处理输入构型。使用程序时，根据提示输入系统构型，包括机械臂数量及臂杆数量，并声明中心体及每个臂杆的刚、柔性等其他系统信息。完成信息输入后，程序会根据输入信息，调用相应的子项，并根据输入信息对子项编号(即程序自动标注子项中的上下角标信息)。完成子项处理后，根据输入系统构型信息，结合上节得出的方程构成规律，自动组合子项，得出目标系统的动力学方程。

程序采用C语言编制，因此具有众多上下角标及特殊符号的数学方程难以辨识。为解决此问题，使程序输出包含符合Latex程序语言规则的“.tex”文本文档，输出符合数学公式阅读习惯的文本。这里使用了Windows操作系统上的基于Latex的Ctex编译器进行二次编译。最终文档以PDF文档形式输出。Latex编辑输出的文档相比DOS直接的输出文档更易于阅读。

使用Kane方程推导该系统动力学方程，所得到的方程与程序输出方程一致，证明了该程序的正确性。

4 软件应用实例

航天器带有一部6自由度机械臂及一部可转动天线，航天器中中心体视为柔性体，机械臂中第1、2、3节臂杆视为柔性体，4、5、6节臂杆视为刚体。通过自动编制程序写出其显式动力学方程。将柔性天线视为一部具有1节臂杆的机械臂系统。输入系统构型之后，程序开始自动编写，编译完成后生成equation.pdf文档。给出部分文档内容,如图4所示。

5 结束语

本文研究了树状构型多体系统动力学显式方程的自动编制方法。首先基于Kane方程推导了链状构型多柔体系统的动力学方程，通过观察、分析方程中各项的物理意义和规律，编写了显式多体动力学方程自动编制程序。程序避免了人工推导复杂多体航天器系统显式方程，为后续动力学建模和分析提供了解析的模型基础。

References)

[1] HOOKER W W,MARGULIES G. The dynamical attitude equation for an n-body satelliteJ]. Journal of the Astronautical Sciences, 1965, 12(4):123-128.2] HOOKER W W. A set of r dynamical attitude equations for an arbitrary n-body satellite having r rotational degrees of freedomJ].AIAA Journal, 1970, 8(7):1205-1207.

[3] KANE T R, LEVINSON D A. Formulation of equations of motion for complex spacecraftJ]. Journal of Guidance and Control, 1980, 3(2):99-112

[4] KANE T R. Partial rates of change of position and of orientationJ]. Bulletin of Mechanical Engineering Education, 1960, 2(17):17-24.

图4 经Latex编译后的部分文档示例Fig.4 An example of text compiled by Latex

[5] KANE T R.Dynamics of nonholonomic systemsJ]. Journal of Applied Mechanics, 1961, 28(4):574-578.

[6] KANE T R, WANG C F. On the derication of equations of motionJ]. Journal of the Society for Industrial and Applied Mathematics, 1965, 13(2):487-492.

[7] ARUN K B. Contributions of multibody dynamics to space flight: a brief reviewJ]. Journal of Guidance, Control, and Dynamics, 2003, 26(3):385-394.

[8] LEVINSON D A. Equations of motion for multiple-rigid-body systems via symbolic manipulationJ]. Journal of Spacecraft and Rockets, 1977, 14(8), 479-487.

[9] SCHIEHLEN W, KREUZER E. Symbolic computerized derivation of equations of motionM]∥MAGNUSK. Dynamics of Multibody Systems.Berlin: Springer-Verlag,1978:290-305.

[10] ROSENTHAL D E, SHERMAN M A. High performance multibody simulations via symbolic equation mainpulation and Kane′s methodJ]. Journal of the Astronautical Sciences, 1986, 34(3):223-239.

[11] LEVINSON D A, KANE T R. AUTOLEV—a new approach to multibody dynamicsM]∥SCHIEHLENW. Multibody Systems Handbook. Berlin: Springer-Veralg, 1990:81-102.

[12] KECSKEMETHY A, KRUPP T, HILLER M. Symbolic processing of multiloop mechanism dynamics using closed-form kinematics solutionsJ]. Multibody System Dynamics, 1997, 1(1):23-45.

[13] BODLEY C S, DEVER A D, PARK A C,et al.A digital computer program for thedynamic interaction simulation of controls and structureJ].Oranization Studies,1978(8):149-168.

[14] 黄文虎，邵成勋. 多柔体动力学M]. 北京：科学出版社，1996:15-18.

[15] PETER C H. Spacecraft attitude dynamicsM]. New York: Dover Publications, 2004.

[16] 胡权，贾英杰，徐世杰. 多体系统动力学Kane方法的改进J]. 力学学报，2011(5):968-972.

HU Q, JIA Y J,XU S J. An improved Kanes method for multibody dynamicsJ]. Chinese Journal of Theoretical and Applied Mechanics, 2011(5):968-972(in Chinese).

(编辑：高珍)

Automatically generating explicit equations of motion for multi-body systems

LI Jinyue,HU Quan*, ZHANG Jingrui

SchoolofAerospaceEngineering,BeijingInstituteofTechnology,Beijing100081,China

The development of the complex multibody spacecraft raises higher requirement to multi-body dynamics modeling and control technology. The explicit dynamics equations of the system are always needed to analyze system′s characteristics and design controllers, but the complexity of system brings difficulty to deriving the equations. In order to solve this problem,the explicit form of dynamics equations′ analytical expression was inferred by using Kane′s method, the chain structure system′s explicit dynamics equations;then, by analyzing this equation, physical meaning and regularities of distribution of each equation item were established;using those regularities, a program that can output the explicit dynamics equations of spacecraft system with tree structure was developed. This program reduces the workload of modeling this type of spacecraft significantly.

multi-body system; robotic arm; explicit formation of dynamics;auto writing; Kane equation

10.16708/j.cnki.1000-758X.2017.0005

2016-07-12；

2016-10-10；录用日期：2016-11-24；

时间：2017-02-16 16:48:33

http:∥www.cnki.net/kcms/detail/11.1859.V.20170216.1648.004.html

国家自然科学基金(11502018，11572037)

李瑾岳(1993-)，男，硕士研究生，ljy19930530@126.com，研究方向为空间机器人姿态动力学与控制

*通讯作者：胡权(1987-)，男，助理教授，huquan2690@163.com，研究方向为航天器姿态动力学与控制

李瑾岳,胡权,张景瑞.显示多体动力学方程自动编制技术J].中国空间科学技术, 2017,37(1)：49-56.LIJY,HUQ,ZHANGJR.Automaticallygeneratingexplicitequationsofmotionformulti-bodysystemsJ].ChineseSpaceScienceandTechnology, 2017,37(1)：49-56(inChinese).

V43

A

http:∥zgkj.cast.cn