基于伪测地线网格划分的优化设计

段玉柱，赵 将

(西安空间无线电技术研究所 神州学院，陕西 西安 710100)

基于伪测地线网格划分的优化设计

段玉柱，赵 将

(西安空间无线电技术研究所 神州学院，陕西 西安 710100)

为减轻反射器重量，并提升系统稳定性，文中基于测地线理论提出一种能有效缩短索网索单元长度的网格划分方法。将理想抛物面切割为几块相同的空间曲面并在曲面上计算测地线，由于两相邻曲面对应测地线在衔接处不光滑，由此产生的网格并非严格意义上的测地线网格，故称之为伪测地线网格。在测地线划分的过程中需要对空间曲面进行分层，考虑到抛物面曲率的变化，每一层的厚度权重系数是不同的，改变厚度权重系数可以达到改变绳索长度、有效面积、型面精度的目的。与现有伪测地线网格划分方法相比，通过优化厚度权重系数可使得绳索总长度缩短、型面误差下降、有效面积增加。

伪测地线；有效面积；精度；绳索长度；权重系数

随着移动通信网络的不断发展，空间可展天线得到了越来越多的应用[1]。与其他固面天线(Solid Surface Reflector)相比,可展天线具有重量轻、口径大、结构简单等优势[2]。可展天线的索网型面一般是由受张力作用的多边形逼近理想曲面形成的，多边形包括三角形、四边形、六边形等，其中利用三角形逼近理想曲面的研究较多，应用较广。1979年，Nayfeh等提出先在锥面上划分三角形网格然后投影到理想曲面形成反射器索网型面[3]；1981年，Agrawal提出在球面上进行网格划分然后投影到理想抛物面形成索网型面[4]；2002年，Tibert提出在xy平面划分三角形网格然后投影到理想抛物面形成索网型面[5]。

测地线源于对地球尺寸与形状的大地测量学，又称为大地线或短程线，可以定义为空间两点局域最短路径，如球面上大圆、平面上直线等。其数学定义为：曲面上测地曲率恒等于零的曲线是测地线，其中测地曲率是指曲线在该点处曲率沿曲面该点处切平面上的投影。考虑到测地线的短程性，测地线索网可有效缩短索网索单元的长度，近年来测地线在网格划分中的应用也展开了研究[6-9]。1997年，Tomsom,M.W提出了伪测地线设计概念[10]；2003年，Tibert提出了准测地线网格的设计方法[11]；2012年，Morterolle提出了准测地线网格的数值找形算法[12]。2013年，B.Yang提出伪测地线网格的参数化设计方法[13-14]。

文中在前人的基础上对伪测地线网格划分过程的参数进行了优化，并结合文献[15]的思路，将球面上求得的节点投影到距理想抛物面一定距离的抛物面。与其它网格划分相比，文中方法得到的网格具有索网索单元长度短、有效面积大、型面精度高的优点。

1 网格划分

1.1 选择拟合球面

对一给定口径D、焦距F的抛物面，选择一球面使它与抛物面在顶点、口径圆处重合，在球面进行节点计算然后投影到理想抛物面进行网格划分。对于给定焦距F和口径D的抛物面，选择参考球面为

x2+y2+(z+R-H)2=R2

(1)

其中

R=2F+D232F

(2)

(3)

1.2 优化权重系数

用过顶点A且位于抛物面上的曲线将球面均分为N块(N可取4、6、8等)。然后将球面沿环向分为M层(M的值与容许误差决定的最大绳索长度相关)由内到外第一环记为第1层，以此类推。图2中蓝线表示分块，红线表示分层。每层厚度系数满足

(4)

图1 参考球面分块及分层

分层后M为最外一层，其内部所包含的面积为有效面积，显然有效面积的大小与各层的厚度权重系数相关。若令M层以前的权重系数为1，则有效面积的大小与wb相关。

考虑到边界绳索太短不利于其与桁架连接，文中假设边界绳索的长度与同等条件下三向网格中边界绳索的长度一致。即令有效口径与三向网格的有效口径一致的情况下得出的权重系数wb为最终值

(5)

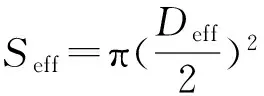
(6)

考虑到三向网格的口径利用率较高，以三向网格的口径利用率为标准，令M层的厚度权重系数 满足

(7)

求得wb的值，并以此划分的网格兼顾测地线性质使得索单元长度最短与三向网格口径利用率高两个优势。

1.3 球面上节点坐标计算

记i层j个节点坐标为[13]Ni,j{x(i,j),y(i,j),z(i,j)}，按照文献[9]的方法可确定节点坐标。

图2 节点坐标计算

(8)

至此完成参考球面上节点的计算并可据此完成球面上网格的划分。

1.4 选择投影面并投影

当完成参考球面的网格划分以后将各节点投影到要求的抛物面上。根据几何关系可得出球面和抛物面上各节点坐标满足

(9)

仿真结果显示：将参考球面上节点直接投影到设计抛物面上得到的索网型面精度比较低。根据文献[15]可知，投影前将理想抛物面沿着开口反方向平移L2/16F后得一新抛物面p，然后将各节点投影到抛物面p上来拟合理想设计面(其中L为投影之前等边三角形边长)，所得结果型面精度最高。但由于文中投影之前参考球面上的空间三角形并非等边三角形，所以不能直接采用文献[15]中的方法，故需优化偏移量，以确定最佳值。以偏移量L作自变量，型面误差作因变量，可得图3所示结果。

图3 偏移量与误差

如图3所示，当偏移量增加时，误差下降，但增加到一定值Lmax时，随着偏移量的增加，误差反而上升，取此时的偏移量为最佳偏移量。即将球面上节点投影到理想抛物面向开口方向偏移Lmax的抛物面上时，误差最小。

2 算例

以一个F=6 m,D=10 m，分块N=6，分层M=5抛物面为例进行计算。

图4 网格平面视图

将本文所提方法与文献[13]及文献[15]进行比较，比较结果如表1所示。

表1 3 种网格划分法比较

由表1可知，本文所提出的方法在同等情况下有效面积比其他两种方法都大；在绳索总长度略大于文献[13]所提及方法的情况下，但精度比其有大幅提升；在精度相当的情况下，绳索总长度与文献[15]中提出的方法相比大幅缩短。

3 结束语

为了获得精度高、有效面积大、索网索单元长度短的网格，文章对文献[13]的算法进行了改进，通过算例验证了所提方法的正确性、有效性及可行性。并得出结论：(1)伪测地线网格划分过程中，有效面积的大小与厚度权重系数相关，可通过优化厚度权重系数使得网格在满足其他限制条件的情况下有效面积达到最

大；(2)在投影过程中，将节点投影到距理想抛物面一定距离的相同曲面上，并以投影后的节点形成的索网来拟合理想曲面可有效降低型面误差。

[1] Gao S S,Clark K,Zackrisson J, et al. Space antenna handbook[M].NY,USA,Wiley Press,2012.

[2] Swanson P N, Gulkis S, Kuiper T B H, et al. Large deployabel reflector (LDR): a concept for an orbiting submillimeter-infrared telescope for the 1990s[J]. Optical Engineering, 1983, 22(6):725-731.

[3] Nayfeh A H, Hefzy M S, Nayfeh A H. Geometric modeling and analysis of large latticed surfaces[J]. Research Gate,1980(3):152-156.

[4] Agrawal P,Anderson M,Card M.Preliminary design of large reflectors with flat facets[J].IEEE Transactions on Antenna and Propagation,1981,AP-29(4):688-694.

[5] Tibert G. Deployable tensegrity structures for space applications[J]. Ceas Space Journal,2002(12):59-68.

[6] 童晶,陈正鸣. 三角网格表面近似测地线的计算[J]. 计算机辅助设计与图形学学报,2008, 20(2):180-185.

[7] 齐贤,黄敬瑜. 三角网格模型上测地线算法的研究[J]. 现代计算机:专业版, 2012(21):15-18.

[8] 施逸飞,熊岳山,朱晨阳,等. 改进的三角网格表面近似测地线算法[J]. 计算机工程,2014,40(11):225-228.

[9] 于方. 三角网格表面任意两点间并行近似测地线算法[J]. 计算机工程与应用,2011,47(10):197-200.

[10] Thomson M W.The astromesh deployable reflector[C].Pasadena,CA:5th International Mobile Satellite Conference,1997.

[11] Miura K, Miyazaki Y. Concept of the tension truss antenna[J]. Aiaa Journal, 1990, 28(6):1098-1104.

[12] Morterolle S, Maurin B, Quirant J, et al. Numerical form-finding of geotensoid tension truss for mesh reflector[J]. Acta Astronautica, 2012, 76(4):154-163.

[13] Shi H,Yang B,Thonson M,et al.Automatic surface mesh generation for design of space deployable mesh reflectors[C].Malaysia:Aiaa/asme/asce/ahs/asc Structures, Structural Dynamics and Materials Conference, Aiaa/asme/ahs Adaptive Structures Conference,2012.

[14] Shi H,Yang B,Fang H .Offset-feed surface mesh generation for design of space deployable mesh reflectors[C].CA,USA:The 14th AIAA Gossamer Spacecraft Forum，The 54rd Structures, Structural Dynamics, and Materials Conference (SDM),2013.

[15] 杨东武.星载大型可展开索网天线结构设计与型面调整[D]. 西安：西安电子科技大学, 2010.

The Optimization of Mesh Generation Based on Pseudo-Geodesic Theory

DUAN Yuzhu，ZHAO Jiang

(China Academy，Xi’an Institute of Space Radio Technology, Xi’an 710100,China)

A new method for minimizing cables length that based on geodesic theory was proposed, which aiming at lighting reflector’s weight and enhancing system’s stability. divide the desired working surface into several parts and draw geodesic lines on them, since the final lines were not smooth enough, the mesh generated by proposed method was not absolutely geodesic mesh net, and named it pseudo-geodesic mesh net. layering was required, in the process of mesh creation, the weight coefficient of layer thickness should not be uniform, when take the surface’s curvature changing into consideration. change of cable length, effective area and surface error can be reached when altering the weight coefficient. shorter cable length, bigger effective area and lower surface error can been achieved, compared whit existing methods, by optimizing the weight coefficient.

pseudo-geodesic; effective area; surface error; cable length; weight coefficient

2016- 04- 24

国家自然科学基金资助项目(11402196)

段玉柱(1989-)，男，硕士研究生。研究方向：空间天线构型设计。

10.16180/j.cnki.issn1007-7820.2017.03.004

TN929.5

A

1007-7820(2017)03-011-03