基于模糊聚类法和互信息法的测温点优化方法

张苗苗，钱 炜

(上海理工大学 机械工程学院，上海 200093)

基于模糊聚类法和互信息法的测温点优化方法

张苗苗，钱 炜

(上海理工大学 机械工程学院，上海 200093)

针对磨床砂轮架系统温度测点的布置会直接影响热误差模型的精确性，提出了一种基于模糊聚类法和互信息法相结合的测温点优化方法。通过计算多个测点的温度变量与变形之间的互信息量，获得其关联度矩阵，确定相关性后初选温度变量。再根据模糊聚类法对初选的温测点进行聚类，并结合温度变量与热变形之间的关联度值提取机床热关键点，从而实现测点优化。通过实验方法测得测温点各时刻温度数据，为机床的结构优化、性能提高提供了改进的依据，进而改善机床的加工精度。

热特性；模糊聚类；互信息法；测温点优化

磨削是机械加工领域的一种重要加工方式，可以使工件表面获得较高的精度，热误差是影响加工精度的制约因素之一。研究表明机床主轴系统热变形对加工精度的影响占到40%～70%[1-4]。减少热变形所带来的影响能够有效提高机床的加工性能。砂轮架热变形大幅度地影响了其加工精度，因此有必要采用一些合理的方法对其热特性进行优化[5-6]。机床热关键点的优化是建立机床热误差模型过程中的一个重要步骤。目前在温度测点优化主要通过理论分析为基础找出最优温度测点和布置大量测温点从中选优。温度测点的选择对机床的实验验证及后续的散热系数的修正和最终的修正结果影响较大，同时测点过多，所需的人力物力也会越多，同时测点之间相关性也会较大，测点过少，不能够准确的获得所需的数据。

本文以M1450B磨床砂轮架为研究对象，为了校正砂轮架有限元模型，使有限元分析更接近于实际情况，提出结合磨床砂轮架系统稳态温度场云图，使用模糊聚类法与互信息量法相结合优化选择测温点，通过实验方法测得测温点各时刻温度数据，对磨床砂轮架系统的热特性有限元模型的对流换热系数进行修正，保证了有限元模型的正确性，为磨床砂轮架系统的结构优化提供参考依据。

1 磨床砂轮架系统的温度场分布云图

对磨床砂轮架系统的热变形分析，其温度场分析是其中最为关键的部分。本文中利用三维建模软件SolidWorks建立磨床砂轮架系统的三维模型，然后导入ANSYS通过对磨床砂轮架系统的温度场分析，得到磨床砂轮架系统整体温度场分布云图，如图1所示。

图1 砂轮架系统整体稳态温度场云图

如图1所示，磨床砂轮架上的温度分布是其电机、主轴系统和砂轮附近温升较为明显，而壳体及主轴箱的部分温升较小，其温度接近于环境温度。主轴箱两端温度偏高，靠近带轮一端温度高于砂轮一端，中间部位温度也呈现梯度变化，整个温度场最高温度以及磨床砂轮架主轴箱体外表面的温度明显升高。根据磨床砂轮架温度分布情况及磨床砂轮架外部结构，选择温度变化较大处作为初选测温点，选定24个测温点作为初选温度测量点，测点位置如图2所示。

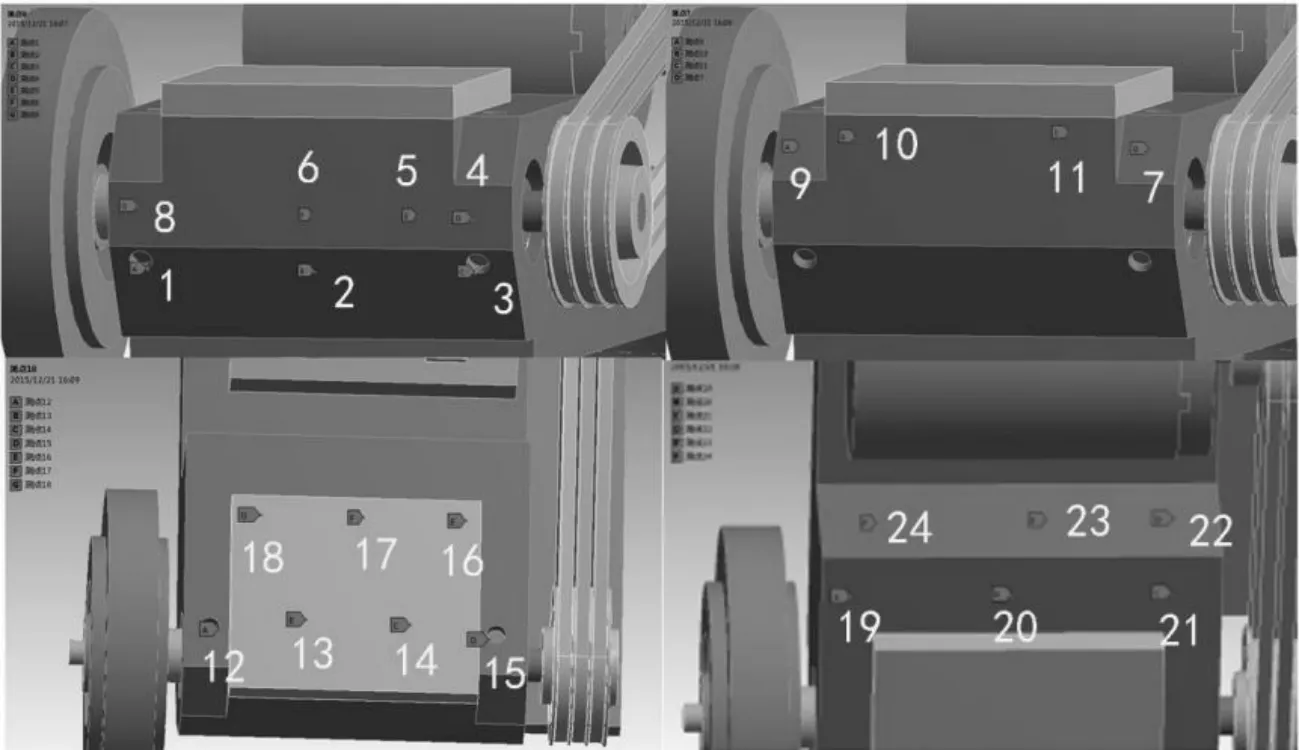
图2 初选测点

2 温度测点优化

根据选定的24初选温度测量点，采用模糊聚类法将初选测温点进行前期分组，再通过信息论中的互信息量求出每组中热变形量与温度之间信息量最大点作为的测温点，从而实现对初选测点的优化[7-15]。

2.1 温度变量的模糊聚类分组

模糊聚类是通过分析各温度变量之间的相关性，利用其相关性建立模糊关系，进而对初选测温点进行分组。具体步骤如下：

计算各初选测点之间的相关系数rij(i>1,j≥N)，其中，rij→±1，两变量之间相关性增大；rij→0，两变量相关性减小。

根据所求相关系数重建温度变量的相似矩阵R=(rij)NN，设温度变量Xi(i=1,2,…N),Xik(i=1,2,…N;k=1,2,…N)，为Xi的n个温度测点温度数据值，其相关系数为

(1)

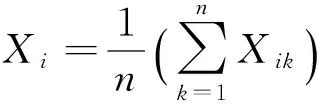
上述计算所得模糊相似矩阵通过矩阵的传递闭包t(R)转换成为模糊等价矩阵。当出现R2(k+1)=R2k时，t(R)=R2k即为模糊等价矩阵。

利用等价矩阵t(R)对温度变量进行模糊聚类分组。在[0,1]内选定一个阈值

(2)

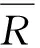
由计算可知取阈值λ=0.997便可得到分组矩阵便可得到分组矩阵，由聚类分析结果可将24个温度变量分为(T1，T3，T14)、(T2，T5，T7，T8，T9，T13,T15，T16，T17，T18，T19，T20，T21，T22，T23，T24)、(T4，T6，T10，T11，T12)3组。

2.2 基于信息论的温度测点

信息论所建立的互信息概念，给出了使用互信息方法定量计算两序列。可用来描述温度测点所提供的关于机床热变形信息量的大小。利用磨床砂轮架系统热特性有限元，对温度测点的测量位置进行优化，通过磨床砂轮架热变形互信息量大小评判温度测点位置优劣。通过互信息概念描述引入信息论中的互信息量来描述计算测点温度和主轴变形的相关性问题[16]。

假设磨床砂轮架上的温度测量点待定为M，M={m1,m2,…，mn}，通过有限元分析获得待选位置上的温度随时间的变化量T，T={T1(t),T2(t),…，Tn(t)}，磨床砂轮架形变量随时间的变化量为Z(t)，各测量位置温度的取值范围为[Tmin,Tmax]，磨床砂轮架形变量取值范围为[Zmin,Zmax]。

每个温度测量点位置温度变化的不确定度使用熵函数表示

(3)

磨床砂轮架变形量的不确定度用熵函数表示为

(4)

通过某温度测点测量值所提供的磨床变形量的互信息量可表示为

(5)

根据式(5)，可计算出通过模糊聚类法所分组中每个磨床砂轮架上的测温点与机床热变形量之间的互信息量I(Y;Ti)，并从中取出互信息量最大I(Y;Ti)I(Y;Ti)。互信息量最大的温度待测点，即为每组初选温度测量点最优测点，将3组初选测温点选出每组中最优的传感器位置。

3 温度测点优化实验

3.1 实验及测试

首先在磨床砂轮架上布置温度传感器，同时安装位移传感器测量砂轮架主轴轴向变形量，如图3所示，将温度传感器安装到磨床砂轮架上的温度测点上，再将位移传感器安装在砂轮架旁边的立柱上，对准主轴上的一点。

图3 温度与主轴轴向移动量测试

3.2 实验结果输出

在电机以转速n=1 460 r/min空载运转下，通过该对磨床砂轮架进行约5 h的温度及主轴轴向变形量的测量，得到如图4所示为温度点与时间散点连续图。可看出测点温度变化呈现一致趋势，但是靠近带轮附近的测点温度最高，且高于其他测点约1 ℃。

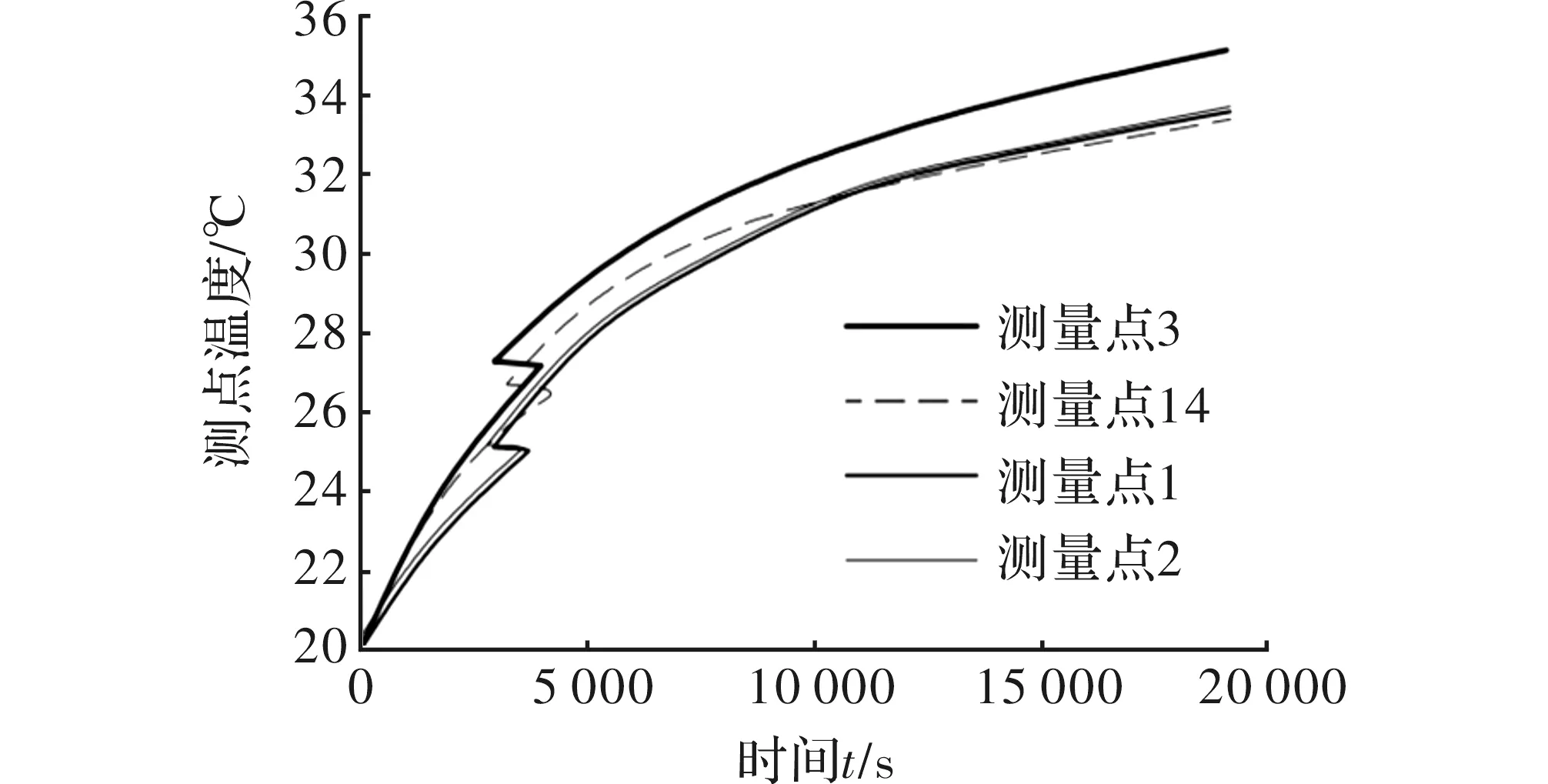
图4 砂轮架测点温度变化曲线

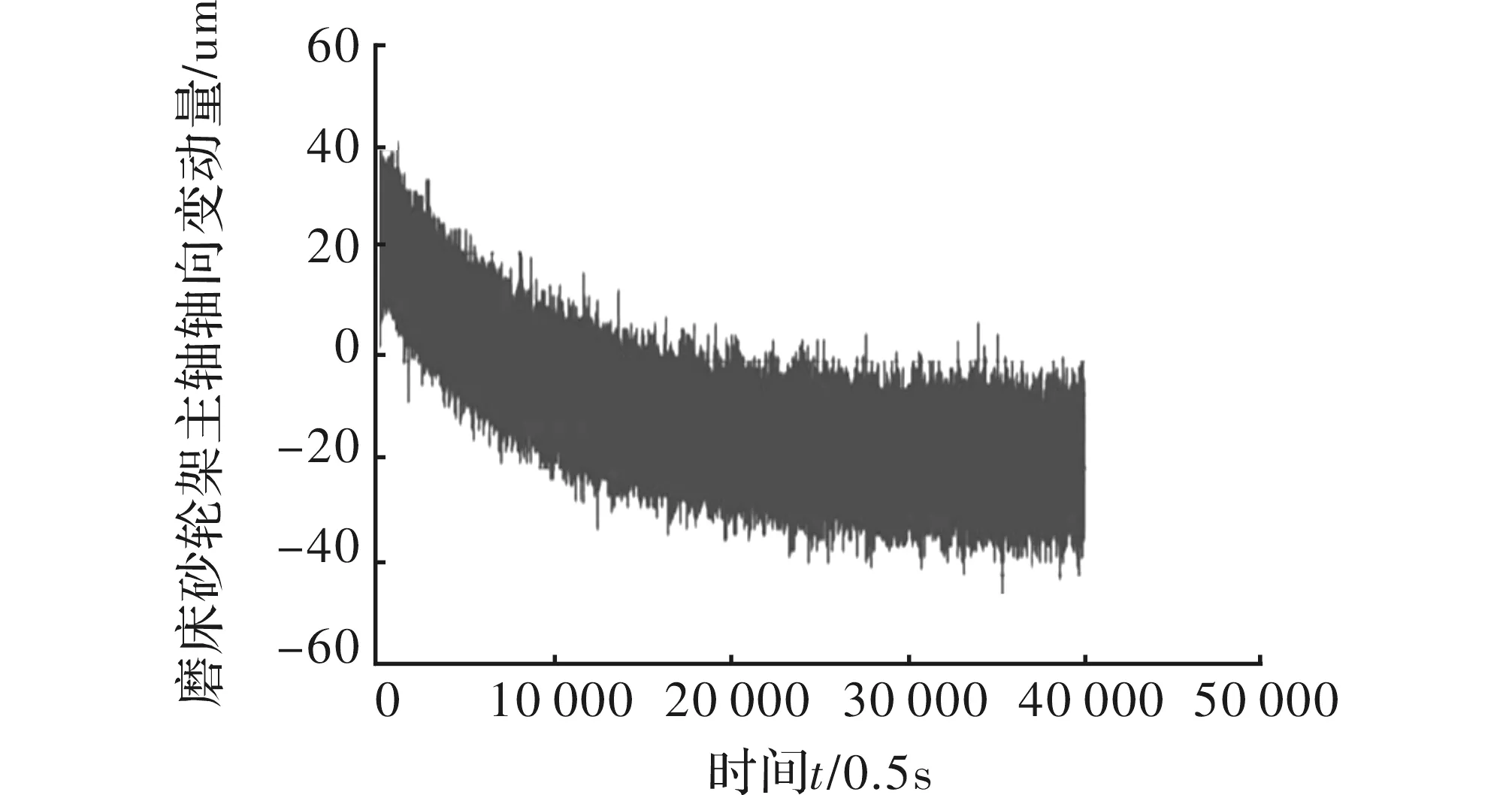
图5 砂轮架主轴整个测量过程轴向变动趋势图

如图5所示，随磨床砂轮架工作趋于稳过程中，砂轮架主轴轴向跳动逐渐加大，点带总体呈现一个向下移动过程，说明主轴随砂轮架工作达到稳态温度场过程中，受温度影响轴向伸长。

3.3 磨床砂轮架实验数据对比

从分析可知，磨床砂轮架主轴轴向伸长量受温度影响比较大。磨床砂轮架系统热分析是一个复杂的过程，所得到的实际结果和分析所得的结果通常有一定的偏差，为使该系统热变形分析结果更加准确可信，必须进行一定的验证。根据温度传感器采集到的温度变化，以及其的位置。在有限元模型上取近似节点作为其3点的温度模拟，温度数据如表1所示。

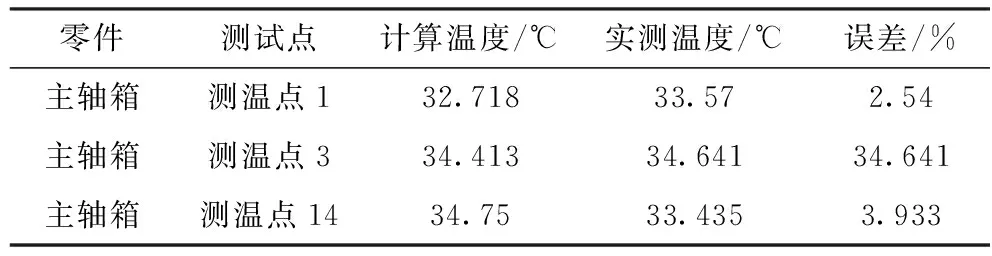
表1 温度数据

由表1可知，有限元分析结果与实际测量结果的误差<4%，虽温度误差相对较小，但为了能将有限元分析的温度场分析结果直接用于磨床砂轮架系统的热变形分析，还需进一步对磨床砂轮架的主轴箱体表面对流换热系数调整，使参数修正之后有限元模型更加接近于实际工况。

4 结束语

本文通过有限元法仿真研究了磨床砂轮架温度场变化，提出结合磨床砂轮架系统稳态温度场云图，选取温度敏感区域中24个温度测点，使用模糊聚类法与互信息量法相结合优化选择测温点，通过实验方法测得测温点各时刻温度数据，为磨床砂轮架系统的热特性有限元模型的对流换热系数进行修正及磨床砂轮架系统的结构优化提供了参考依据，可进一步提高加工机床的精度。

[1] 李永祥,杨建国,李昱瑶,等.基于灰色系统的机床热误差建模研究[J].武汉理工大学学报,2007,29(1):58-61.

[2] 李永祥,童恒超,曹洪涛,等.数控机床热误差的时序分析法建模及其应用[J].四川大学学报:工程科学版,2006, 38(2):74-78.

[3] 李永祥,杨建国.灰色系统模型在机床热误差建模中的应用[J].中国机械工程,2006,17(23):2439-2442.

[4] 李永祥,杨建国,郭前建,等.数控机床热误差的混合预测模型及应用[J].上海交通大学学报,2006,40(12):2030-2033.

[5] 张祥雷,冯伟,陈站,等.磨床主轴热特性分析及热变形补偿策略[J].机电技术,2014(2):2-3.

[6] 杨光,杜计划.基于ANSYS的高速磨床砂轮架的结构分析和改进研究[J].机械研究与应用,2008,21(4):93-95.

[7] 赵瑞月.大型龙门数控机床温度测点优化与热误差建模技术研究[D].南京:南京航空航天大学,2012.

[8] Ramesh R,Mannan M A,Poo A N.Error compensation in machine tools- review Part II:thermal er-rors[J].International Journal of Machine Tools& Manufacture,2000,40(9):1257-1784.

[9] 史玉峰,靳奉祥.数字信息模式识别理论与应用[M].北京:科学出版社,2007.

[10] 杨建国,邓卫国,任永强,等.机床热补偿中温度变量分组优化建模[J].中国机械工程,2004,15(6):478-481.

[11] Lo C H,Yuan J,Ni J. Optimal temperature variable selection by grouping approach for thermal error modeling and compensation[J].International Journal of Machine Tools and Manufacture,1999,39(9):1383-1396.

[12] Fraser S,Attia M H,Osman M O.Modeling identifiation and control of thermal deformation of machine tool structures, PartⅡ:generalized transfer functions[J].ASME Journal of Manufacturing Science and Engineering,1998,120(3):623-631.

[13] 吴昊,杨建国,张宏韬,等.精密车削中心热误差鲁棒建模与实时补偿[J].上海交通大学学报,2008,42(7): 1064-1067.

[14] 闫嘉钰,张宏韬,刘国良,等.基于灰色综合关联度的数控机床热误差测点优化新方法及应用[J].四川大学学报:工程科学版,2008,40(2):160-164.

[15] Choi K J,Lee D G.Thermal characteristics of the spindle bearing system with a gear located on the bearing span[J].International Journal of Machine Tools&Manufacture,1998,38(9):1017-1030.

[16] 李郝林,应杏娟.数控机床主轴系统热误差温度测量点的最优化设计方法[J].中国机械工程,2010,21(7):804-808.

Investigation on Optimization of Temperature Measurement Key Points Based on Fuzzy Clustering Analysis and Mutual

ZHANG Miaomiao，QIAN Wei

(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

According to the arrangement of the temperature measuring can directly affect the accuracy and robustness of Thermal error modeling,the paper put forward the a new method of using fuzzy clustering method and mutual information method for the optimization of temperature measuring points. analysis data of all temperature measuring points is calculated to obtain correlative matrix and determine the correlation．The temperature measuring points are optimized with correlative matrix by combining the temperature variables clustered based on the fuzzy clustering method. Meanwhile,the experiment measured measuring points’ temperature.It provided a basis for the structure optimization, performance improvement of machine, and then improved the machining accuracy of machine tools.

thermal characteristic; fuzzy clustering; mutual information method; optimization of temperature measuring points

2016- 04- 22

张苗苗(1993-)，女，硕士研究生。研究方向：机械设计。钱炜(1964-)，男，硕士，副教授，硕士生导师。研究方向：机械设计及理论。

10.16180/j.cnki.issn1007-7820.2017.03.010

TP391.41

A

1007-7820(2017)03-033-04