让几何直观成为数学思维习惯——小学数学培养学生几何直观能力的实践研究

丁国成

（浙江省余杭双溪小学）

一、一道数学题的启示

一套衣服，上衣每件48元，裤子每条36元，用1000元钱买这样的12套衣服够吗？（请作图表示你的解决方法）

这是四年级的一道数学题。括号中“请作图表示你的解决方法”这个小小的要求，对学生造成了很大的困扰。

1. 无从下手

抽取四年级100名学生的题目进行调查分析，发现：画图31% ；列表 16%；算式对，不画图47%。这31%的画图的学生中，完全能用图形或符号描述和分析问题的只有三分之一左右。更多的学生，面对“请作图表示你的解决方法”无从下手。

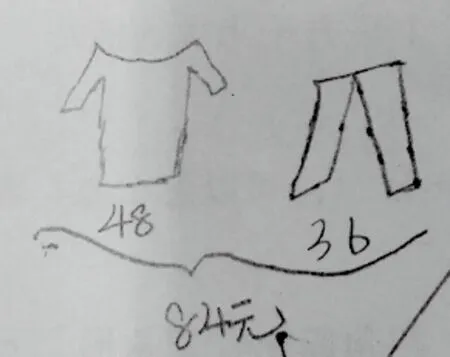
2. 图不表意

像这样画一件衣服和裤子的学生不在少数，学生只是单纯地为“作图”而“作图”，这样的图没有起到描述数学问题的作用。

究其原因是学生没有借助图形理解、分析问题的意识，缺乏相应的画图能力，没有形成几何直观的数学思维习惯。

二、立足课标，“几何直观”之内涵解读

课程标准明确提出“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要的作用”。可以理解为，借助图形描述，把抽象的问题直观化，利用图形寻找解决问题的途径和方法，最后能直观地理解抽象问题。

三、小学数学让“几何直观”成为思维习惯之策略研究

研读课标，可以发现，几何直观是一种意识，也是一种技能与能力，更是一种思维方式。在我们的实践过程中，从以下几方面入手。

（一）突显价值，逐步形成以形助思的意识

“几何直观”的意识指在数学学习中，学生面对数学问题，能感受到可以通过实物、图形、符号等直观形式分析和解决问题。要让学生感受到几何直观的价值，学生才会有意识地去往几何直观靠近。

1. 感受其形象化

用图形描述数学问题，用图形说话的能力，这是几何直观的内涵之一。学生要形成“几何直观”的意识，逐步学会从问题到图形的描述，要从一年级开始。

这类问题对于一年级的学生来说，常常是不知所措。教师在教室里模拟，学生也是排队的时候清楚，回到题目又迷雾重重，这时可以引导学生画图。

学生经过尝试、交流，可以得到这样的两幅图：

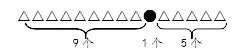
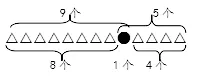
在这里，学生用不同的图形表示主题图中“我”和其他同学，并用大括号准确地表示出了两幅图中“9”和“5”两个数字所包含的学生，准确地表达出了“几”和“第几”的不同。学生要形成几何直观的意识，首先需要在日常的学习中多加运用，学会从问题到图像。

2. 经历其抽象化

低年级学生喜欢用简单的图形去表示数学问题中的具体事物，从而理解其中的关系。在学生掌握一定的画“示意图”的技能后，适时引入“线段图”，让学生经历“文字—符号—图形”的过程。

案例：求一个数的几倍是多少？

出示：7只蜗牛，瓢虫的只数是蜗牛的3倍

教师：你会画出瓢虫的只数吗？

展示反馈：

第一种：画了两只后，就用圈圈代替。

第二种：直接用三角形代替。

第三种：直接用线段图表示了蜗牛和瓢虫的数量。

教师：比较刚才的三种方法，你比较赞同哪一种？说说你的原因。

学生：第二种，又简单，又清楚。

学生：第三种的线段图，我觉得也没问题，我们都能看出来什么意思。

教师：现在蜗牛的总数有500只，你会选择用什么方法来表示？

课件演示，用直条覆盖原先的圈圈，形成一幅直条图，把直条进行压缩变形，形成线段图。

7 只 7 只

在这个过程中，教师抓住契机，从直条图过渡到线段图，让学生体验从形象到抽象的过程，经历“几何直观”的思维活动方式。

3. 体验其简明化

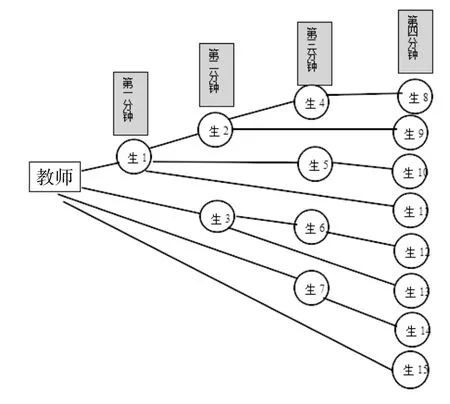
数学文字的抽象、数量关系的复杂给学生分析理解问题带来一定的困难。通过几何直观把抽象的数学问题与直观的图像表达结合起来，使得题目中的数量关系简单明了，突破理解上的难点。如经典案例“打电话”：

学校合唱队有15人，暑假有紧急演出，老师要尽快通知每个队员，用打电话的方式，每分钟通知1人，至少需要多少分钟？

类似这样类型的题目，在比赛的场次等数学广角的领域比较多。在课堂教学小结中，应该问一问：没有图能说清楚吗？真切感受图形给学生的帮助，加深对应用画图策略的价值的直观体验。

（二） 重视画图，培养学生用图说话的能力

几何直观需要用图形把数学问题形象直观地展现出来，要形成对数学问题与图像之间相互转化的能力，就需要在教学中对学生进行画图策略的指导。

1. 积累“图”的经验

当前，我们使用的人教版教材中采用了大量的主题图，几何直观的内容俯拾皆是。在“数的认识”中教材大量采用了小棒、方块等对应的几何模型。用好这些主题图，可以使学生积累丰富的图式经验，提升其几何直观能力。

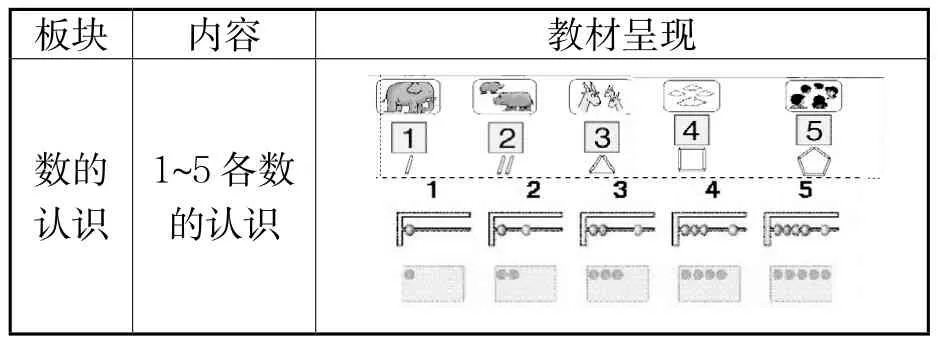
板块____________内容_教材呈现数的认识1～5各数的认识

案例：5的分合

1. 屏幕依次出现5个苹果，最后形成一个“5”字。接着又出现了两个袋子。

师：猜猜每个袋子里可能会有几个苹果？

2.如果用“○”表示苹果，你还会研究吗？

学生使用以下的学习材料独立研究，教师巡视。

几何直观可以追溯到“5以内数的认识”，分析主题图，可以发现，教材以现实情境为起点，帮助学生形成了数大小的表象。到了“5的分合”就让学生经历从实物直观，发展到符号直观，并为今后的图形直观开始积累经验。

2. 拓宽“图”的理解

图的内容：几何直观中的几何指图形，主要指点、线、面、体以及以上四要素组成的其他几何图形。但是作为几何直观中的“图形”并非局限于此，只要能让学生借助用于“描述、分析问题”的图都属于这个范畴。

如“倒推策略”：小明原来有一些邮票，今年又收集了24张。送给小军30张，还剩52张。小明原来有多少张邮票？

在这里，对于解决问题中的倒退策略的运用，教师退回到起点，顺着思维把数量变化的过程表达清楚，再进行倒推，这样才有依据。这时，可以指导学生用箭头图描述数量变化的过程。

3. 重视“图”的过程

课标指出：数学学习内容不仅包括数学的结果，也包括数学结果形成过程和蕴含的数学思想方法。因此教学中，既要重视结果，又要重视获取知识过程。想象、画图是学生思维的载体，突显思维的痕迹。

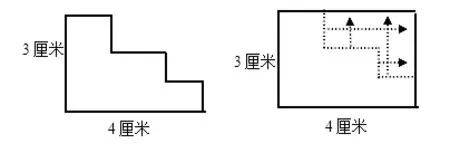
如：求不规则图形周长

不规则图形的计算中无论是周长计算还是面积计算，基本思路可以分为剪拼和转化。特别是转化的过程，语言表达是不及画图准确的。“求不规则图形周长”根据每条边的长度来计算的思路是行不通的。利用转化的策略把它变成一个新的图形就可以了。在交流的过程中，运用课件动态演示转化的过程，有效地在学生的头脑中建立平移转化的表象。

（三）内化思维，形成下意识的思维习惯

通过从低年级开始的用图形表达自己的意识，逐步学会运用几何直观分析数学问题，最终把几何直观内化为一种下意识的、主动的数学思维习惯。

1. 沟通一种联系——抽象与直观

学生借助图形直观进行数学思考，首先需要把研究的“对象”抽象成为“图形”，把“对象之间的关系”转化成“图形之间的关系”，这样就把要解决的具体情境问题转化为具体的图形的数量或位置关系的问题，可以让学生把握问题的本质。

学生在想象、操作、直观表征数学问题的过程中，要逐步建立抽象与直观之间的联系，掌握文字语言、符号语言和图形语言之间相互转化的能力。

如“乘法分配率”的教学中：

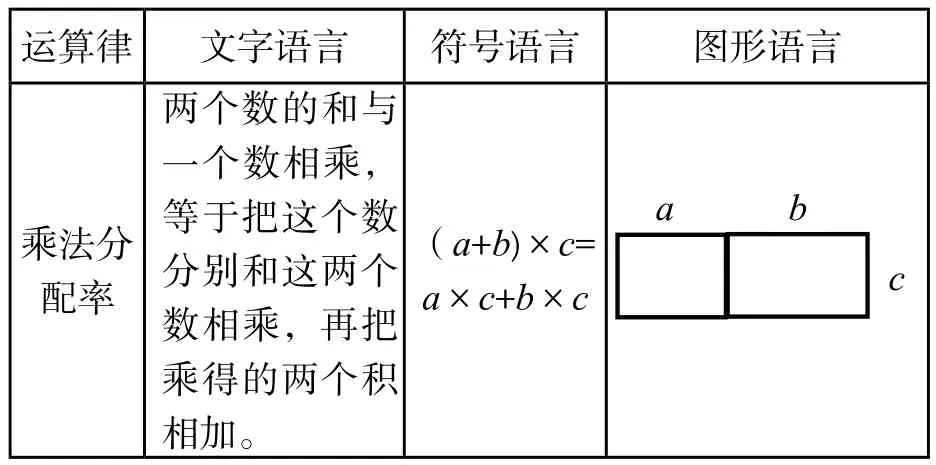
运算律 文字语言 _符号语言_________________图形语言乘法分配率两个数的和与一个数相乘，等于把这个数分别和这两个数相乘，再把乘得的两个积_______相加。_________________________________（a+b)×c=a×c+b×c

在这里，通过归纳整理，用直观的方式建立符号意识，让学生充分感受符号与图形的使用是进行数学思考的重要方式。

2. 建立一种观念——空间观念

在几何图形这一领域内部也需要几何直观进行理解分析。这就要求学生具有很好的空间想象能力，能根据物体特征想象出几何图形，所以学生在学习活动中要参与各种几何活动，注重引导学生将活动过程中对图形的感受与有关知识建立联系。

如“直线、射线和线段”的教学中，可以通过一系列的图片，在视觉上给学生们以直观的认识，从而引出“直线”的概念，使学生轻易发现直线的特点。其实直线是一个理想化的概念，凸显几何直观地感受显得尤为重要。引导学生通过亲身触摸、观察、想象、制作和实验，把视觉、听觉和触觉等协同起来，从而掌握图像特征，建立空间观念。

在学习中，学生的操作以及运用画图表示几何内容的空间形式与位置关系等活动经验越丰富，空间观念的建立越厚实，几何直观的水平就会越高。

3. 形成一种视角——数形结合

数学家华罗庚曾说过：数缺少形时少直观，形缺少数时难入微。数形结合是对知识、能力的贯通式的理解与认识。

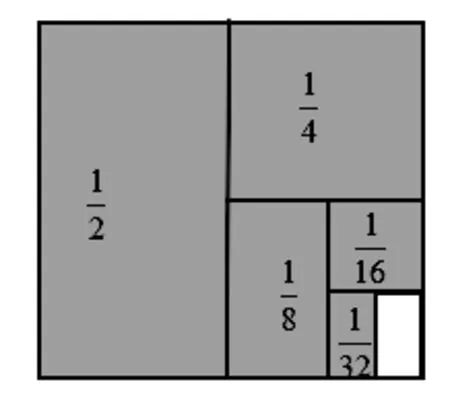
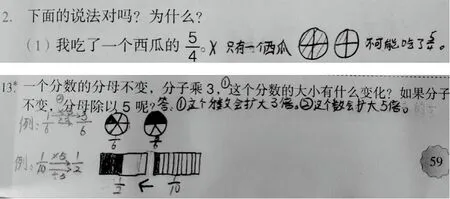
学生常规的做法是通过通分进行计算。借助这一直观图就可以把复杂的计算转化成简单的计算：

像这样的例子不胜枚举，在这里就要用好教材，挖掘教材，在循序渐进中，通过学习，逐步形成一种对数与形之间的化归与转化的意识和解决数学问题的视角。

四、让几何直观成为数学思维习惯之研究收获

通过借助几何直观助力数学理解，循序渐进，逐步提升学生几何直观数学思维习惯的形成的策略研究，我们惊喜地发现：学生画图意识提高了，会主动运用图形理解题目的意思，借助示意图，分析数量关系，学生对图形之间的沟通能力提高了。

学生课堂作业

1.增强画图意识

在课题实施过程中，我们可以发现，学生只埋头苦思的想象少了，知道想一想、画一画的过程中，体验到了画图的乐趣。

我们选择了五年级的一个班级，进行了测试，收齐草稿纸时，发现，草稿纸上留下画图痕迹的学生比例明显提高。

2.提升思维能力

从实验班与对比班课堂检测情况分析显示，实验班学生示意图的描述、分析问题的切合度都明显优于对比班。从实验班与对比班期末测试成绩的数据对比发现：实验班的各项优秀率均高于对比班，并且随着年级的升高差距明显。