把握核心概念 创设多维通道 催生素养落地——基于学生认知心理“解决问题”教学路径设计

马 理

（浙江省杭州市胜蓝实验小学）

“解决问题”教学旨向是通过数学教学帮助学生思维，让学生的思维逐步变得更清晰、更全面、更深刻、更合理。因此，“解决问题”教学是落实学生数学核心素养培养的重要载体。

一、“解决问题”教学在发展学生数学素养中的意义

“解决问题”教学在新教材编写中有着非常明显的特征，例如提供解决问题的一般步骤，体现清晰有序的思考；提供丰富的解决问题的方法，体现合理全面的思考；为学生发现问题、提出问题提供了贴近学生生活经验的素材和情境，体现数学地观察，养成数学的理性精神等，这些都是为实现“解决问题”的课程目标服务的，都表达了数学教育正致力于提高学生的“数学核心素养”。

在教学中，“解决问题”不仅仅包含解决某个问题，而是从数学的视角去发现问题、提出问题、分析问题、解决问题。它着力培养学生数学的眼光、数学的思维、数学的语言。因此史宁中教授将数学学科的核心素养解读为三句话：用数学的眼光观察现实世界，用数学的思维分析现实世界，用数学的语言表达现实世界。“解决问题”教学，更关注问题解决的过程——探索、思考、交流、回顾反思。在整个学习活动中，学生通过建立系统的思维方式，来体验知识间的联系，理解知识的价值。“解决问题”是复杂的思维过程，学生需要运用抽象、归纳、类比、演绎等数学思想方法。

显然，教材赋予“解决问题”教学在发展学生的数学素养中的意义非凡。“解决问题”教学能够使学生获得自然的数学知识的同时，获得数学的思维习惯，将数学思考和生活实践中的学习有效结合，让学生获得相互联系的知识结构，帮助学生理解知识的价值，从而发展他们的实践创新能力和科学精神。

二、“解决问题”教学内容在单元体系中的地位和价值

新教材对运用所学知识解决问题教学内容的编排，突破传统应用题教学内容的束缚，在数与代数、图形与几何、统计与概率的各领域都为学生安排了从生活中发现问题、提出数学问题的丰富素材和情境，培养学生提出问题、解决问题的能力。

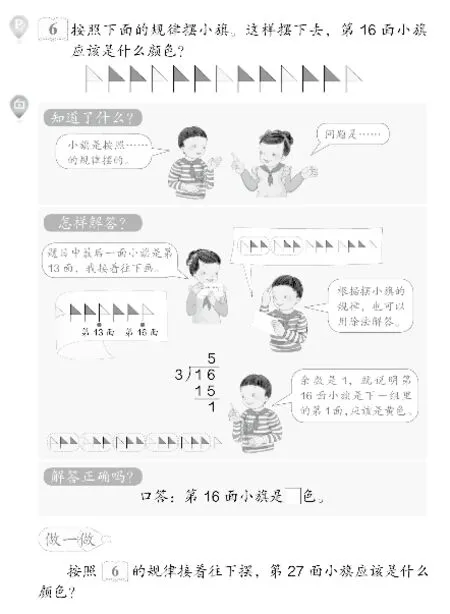
二年级下册《有余数除法》单元“解决问题”教学内容

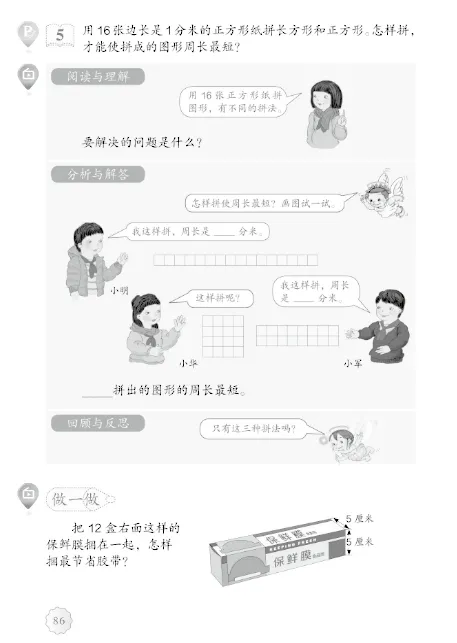
三年级上册《长方形与正方形》单元“解决问题”教学内容

五年级下册《分数的意义和性质》单元“解决问题”教学内容

从上图中可以看到，新教材在各个内容领域加强了对解决问题能力的培养，将培养“四能”（发现问题、提出问题、分析问题、解决问题能力）的教学与各部分知识的教学有机结合。教材循序渐进地提供解决问题的一般步骤，低段教材提供的“你知道了什么”“怎么解答的”“解答正确吗”来引导学生思考。中高段教材提供的“阅读与理解”“分析与解答”“回顾与反思”教给学生解决问题的基本方法。一般“解决问题”教学都安排在每个单元的最后几课时，目标是让学生运用所学知识去解决问题，感受数学学习的价值，增强数学学习的兴趣，深化知识理解，发展数学思维。且每个内容都有其所侧重的思维培养目标，如上图中《有余数除法》单元解决问题侧重建立基本除法问题模型，三年级上册《长方形与正方形》单元中的解决问题侧重感受解决问题策略，五年级下册《分数的意义和性质》单元中解决问题则侧重深化核心知识——分数。

三、“解决问题”学生认知心理分析

早期的教育家从不同的视角分析解决问题的认知过程，著名的有数学问题解决四段论模式。认知心理理论认为，在问题表征阶段，当学生阅读问题时，会在建构的数学表征与文本库之间多次往返。这意味着学生是在不断地更新完善问题表征过程中，逐步加深对问题的理解的，以丰富的表征为基础建构起问题模型。

美国现代认知心理学家西蒙也认为：表征是问题解决的中心环节。能否正确表征问题是解决问题的关键，学生对问题的正确表征，就是用自己的方式重新组织问题情境中的信息，并根据自己的经验和知识对有关信息进行区分和整理，明确信息与问题是否相关，寻找解决问题的突破口，逐步形成解决问题的思路。

布鲁纳为代表的认知理论认为，数学学习过程是一个数学认知过程，数学教育的根本是发展学生的数学认知结构。数学问题解决的过程，就是新旧知识认知结构相互作用，最后升级为新的认知结构。

数学家张奠宙先生提出数学教学的问题驱动原则，它是指在教学中要有“有层次、结构化、可扩展、能持续”的问题或问题系统贯穿整个教学，把学生的思维引向深入，从而最大限度地激发其对问题的探究、体悟和理解教学内容的本质。

根据认知心理理论，笔者认为“解决问题”教学应该关注以下方面：

（1）好“问题”驱动问题的探索。设计好“问题”，让“解决问题”的过程有意义、有意思，更好地推动学生思维发展。

（2）重视“问题表征”策略的积累。表征问题是解决问题的关键环节，在教学中需要加强表征问题的策略的指导，有序地引导学生掌握多种形式表征问题的方法，不断地让学生感受到多元表征之间的转换，逐步提高解决问题的能力。

（3）以问题为载体着力知识结构化。解决问题过程是数学知识结构化的过程。应着力于沟通知识、策略、方法间的联系，形成体系。

四、基于学生认知心理设计“解决问题”教学

1. 追本溯源，厘清三“问”

数学学习需要有贯穿整个教学的“好”问题，才能将学生的思维引向深入。在“解决问题”教学中能驱动学生思考的问题非常重要。在设计问题时，教师要先追本溯源，厘清下面三个“问题”，才能设计出能引领整节课的好问题。

（1）知识本源问题。“解决问题”教材的资源往往带有丰富素材和情境，深刻理解所教学的知识内容的数学本质，准确把握学科本源问题，教师才清楚自己到底是“教什么”。

（2）学习起点问题。要实现每位学生的思维都动起来，必须要了解学生的真实起点在哪里，困惑会是什么，教学才能真正驱动学生自主学习行为。

（3）探究引领问题。这是教学层面的核心问题，与情境设计相结合，让学生能自发地进入“有意思”的问题探索。

三“问”关系图

教师要设计好探究引领问题必须深入思考知识本源问题，也就是“教什么”，还有思考学生现有的学习状况，才能明白自己该“怎么教”。

案例1 三年级上册《分数的初步认识》单元的解决问题

《求一个数的几分之几是多少的简单分数问题》是通过解决问题的形式，进一步理解分数的含义，同时用分数的含义来解决问题，即用平均分的概念来解决“求一个数的几分之几是多少”的简单实际问题，它的知识本源是“平均分”。学生已有的起点是已经学习了平均分问题和初步理解“分数的意义”，已有了“归一”问题的模型，在深入理解了本源问题和起点问题后，在教材创设的贴近学生生活的“男女生人数”问题情境——12名学生，其中是女生，是男生，男女生各有几人？——抓住知识本源和学生起点提炼出探究引领问题，即“其中是女生，是男生是什么意思？你怎么表达是女生的？为什么？是男生呢？”引导学生用画图来辅助表达可以较好地抓住问题核心，在反馈中借助图形表征，让学生充分交流表达，顺利过渡到用算式表征，初步体验简单分数问题的模型。

“解决问题”教学，是展开数学课程的问题探索，是用数学去解决生活问题，具有浓浓的数学味。认真解读思考教学内容的知识本源、学生起点，以此为基础设计才能生活地、新颖地、具有高思维含量地主探问题。

2.打造多维通道，拉长问题体验

（1）构建“半结构化”开放式情境

突破单纯文字问题的形式，用“半结构化”开放式任务情境是问题呈现的重要途径。研究者发现，在“半结构化”的开放式任务情境中，问题提出和解决活动能促进学生学习创造性和批判性思维。

案例2 三年级下册《面积》单元的解决问题：《用面积知识解决问题》

环节一：提出问题，探索起点

出示情境（见图）：小南用长方形卡纸剪正方形的数字卡片。卡纸的长是8厘米，宽是6厘米。一张正方形纸片的边长是2厘米。

看了这些信息后，你能提出什么数学问题？

（学生根据信息提出以下问题）

①长方形卡纸的面积是多少？

②长方形卡纸的周长是多少？

③正方形的数字卡片的面积和周长是多少？

④一共可以剪几张数字卡片？

说说问题是根据哪些信息提出来的，引导学生关注信息之间的关系。

这个环节情境呈现的问题就是“半结构式”的，先出现信息，进行“信息解读”，再用“根据信息提出问题”的操作方法，让学生信息解读自我需求加强了，体会问题的真实性和生成性，培养学生从信息到问题的推理思维。

（2）创设“支点”，拉长思维过程

学生思维是由简单到复杂，由具体到抽象，由感性到理性的。在思维的发展过程中，教师要给学生在思维过程的“支点”，学生借助这个“支点”来学会思维，慢慢提高必要的数学素养。这个“支点”就是基于学生学习现实认知的问题材料，搭建思维的“支点”，就是帮助学生跳过一个个学习上的“坎儿”，学生在不断完成新问题的挑战，慢慢积累数学经验，沉淀数学素养。

案例3 继续以三年级下册《面积》单元的解决问题：《用面积知识解决问题》为例

环节二：理解方法，体会不同的解题思路

围绕“一共可以剪几张数字卡片？”学生独立尝试，要求简单地写出（画出）思考过程。交流引导以下两种方法：

预设一：8×6=48（平方厘米），2×2=4（平方厘米），48÷4=12（张）

预设二：用画图表示，得到结果

8÷2=4（张），6÷2=3（张），4×3=12（张）

讨论两种方法对吗？都是怎样思考的？

得出方法一的思路是:大图形的面积÷小图形的面积

方法二的思路是：行的张数×列的张数

环节三：解决生活问题，再次感受两种不同解题思路

像这样的问题，生活中有吗？学生举例。

呈现教材例题：“客厅的长是6米，宽是3米，用正方形的地砖铺地，地砖的边长是3分米。铺客厅地面一共要用多少块地砖？”请学生独立尝试完成解答，反馈时引入第二种方法的图示。

①教师引导对比，说说这个问题和我们“用卡纸剪数字卡片的问题”有什么相同点和不同点。

小结：解题方法（思路）一样，但这道题需要转化单位。

②再次对比：那么第一种方法和第二种方法有什么共同点呢？它们都有除法算式，表示的意义分别是什么呢？

环节四：再次探索，丰富感性经验

出示情境：小北用长方形卡纸剪正方形的数字卡片。卡纸的长是10厘米，宽是9厘米。一 张正方形纸片的边长是3厘米。一共可以剪几张数字卡片？

学生自主解决后反馈交流。重点比较两种方法的异同。

方法一：10×9=90（平方厘米），3×3=9（平方厘米），90÷9=10（张）

方法二：10÷3≈3（张），9÷3=3（张），3×3=9（张）

让学生用画图表示，说明得到结果。

到底可以剪几个呢？哪种方法对是的？为什么？

生活中的问题会出现这样的情况吗？

与“小南剪卡片的问题”对比，为什么第一题两种解法都可以，而这道题只能用第二种方法呢？想想什么情况下可以用“大图形面积包含着小图形面积”这种方法呢？

环节五：变换情境，拓宽思路，发展思维能力（略）

【思考】学生解决这样的问题的两条基本途径是逐步感受到并加深理解的。第二种方法是普适的方法、一般的方法，更符合真实问题的解决，但它相对来说比第一种方法结构上更复杂些，所以只有在经历解决问题过程时，当直接用“大图形面积÷小图形面积”不能解决时，需要研究大图形的长、宽与小图形边长的关系，于是，画图、以数形结合的思维方式帮助学生理解信息之间的关系，准确地找到解题的突破口。

以上教学活动中，学生的思维不再是一步到位的，而是尽可能地拉长思维过程，从基础的图示化问题，到具体生活问题，再增加变式的图示化问题，最后再回到生活问题，不断积累表征问题和分析问题的基本活动经验。通过四个问题的解决，借助每个问题解决过程的充分探讨、体验，一层层地引导学生感受问题解决各环节的操作要点。

（3）多形式表征，打造多维通道

教学中教师要适当放慢脚步，用图示、表格、文字等不同的表述方法，感受相同问题不同表征，和不同问题表征之间的转换，循序渐进推进学习进程，让学生能从容地找到适合自己解决或思考问题的思维通道，这也是培养学生解决问题的关键能力。比如，上例《用面积知识解决问题》的教学中引导学生不断地在图示、文字和算式的表征中对比理解两种问题解决方法，第一种是大面积里面包含了几个小面积就是需要铺几块砖；第二种方法中的除法表示大图形的长里面包含了几个小图形的边长，宽包含了几个小图形的边长，再相乘求出一共有块数。在问题解决中打造多维通道，引导学生找到这些方法间的内在联系，让彼此的方法能有一条线串起来。并在“同中求异”“异中求同”的问题驱动下，慢慢养成数学的思维习惯，以此来使学生的数学素养提升成为可能。

3.沟通“联系”，着力核心知识的结构化

新教材将“解决问题”视为把先前所获得的知识用于新的、熟悉或不熟悉的情境的过程，体现以“问题为中心的学习”。因此，“解决问题”教学需立足于核心知识、方法，可以看作是将知识结构化的过程，是知识在解决问题的过程中的联系和沟通，使学生的知识结构在运用中形成体系。

案例4 三年级上册《分数的初步认识》单元的解决问题教学片段

环节三 ：对比练习

你发现了什么？这几题有什么相同与不同？

你发现了什么？这几题有什么相同与不同？

【思考】在“求一个数的几分之几是多少”问题的数学模型已经初步建立起来以后，学生要在应用模型的过程中真正建模。笔者设计三个层次：第一层次是总数和平均分的份数（分母）不变，变的是取了几份（分子）；第二层次是对比练习是总数和取了几份（分子）不变，变平均分的份数（分母）；第三层次是平均分的份数（分母）和取了几份（分子）都不变，总数不同，让学生不仅体会解答方法，更要理解解答的道理，在比较中让学生更多地感受“变”与“不变”，从而更深层次地理解体会核心概念——分数。

“用分数解决分数问题”一课的核心知识是“平均分”和“分数的意义”，分数的意义本质上也就是“平均分”，在引入中将平均分和分数的意义进行比较，说说：“你有什么发现？为什么题目不同答案却是相同的？”在探究后说说：“我们刚才在理解分析问题时用到了什么方法、什么知识？”在总结时说说：“今天学习的内容与我们以前学习的什么知识本质上是相同的？”让学生体会分数的有关知识及应用都是以平均分为起点的，抓住核心知识，并将分数问题与归一问题联系起来，形成知识的结构化理解，建构知识体系。

[1]唐彩斌. 从小学数学视角探讨核心素养的双重关系与四大意识[J]. 小学数学教师，2016（7、8）.

[2]边巨星，汤骥 .“核心素养”下的教学再出发[J].教学月刊，2017（1、2）.

[3]朱德江. 新课程下“解决问题”的教学与指导策略构建[J]. 小学教学，2007（10）.

[4]许自强 .国际数学教育改革的新趋势：聚焦“问题提出”[J].小学数学教师，2016 （7、8）.