基于粒子群优化的SVR风电功率超短期预测

徐炜君，裴 欢，魏 勇

(1.东北石油大学秦皇岛分校电气信息工程系，河北 秦皇岛 066004；2.燕山大学信息科学与工程学院，河北 秦皇岛 066004)

基于粒子群优化的SVR风电功率超短期预测

徐炜君1，裴 欢2，魏 勇2

(1.东北石油大学秦皇岛分校电气信息工程系，河北 秦皇岛 066004；2.燕山大学信息科学与工程学院，河北 秦皇岛 066004)

建立了风电功率预测系统并提高其预测精度和预测速度.分析影响风机出力的主要因素并结合风电场实测风速数据和环境参数，提出了一种基于粒子群优化的SVR风电功率超短期预测模型，该模型可以有效地优化支持向量回归机(SVR)的主要参数.通过与遗传算法优化的预测模型(GA-SVR)进行比较，发现该预测模型在超短期风电功率预测上有较高的预测精度和运算速度.

风力发电；超短期预测；支持向量回归机(SVR)；粒子群优化算法

0 引言

随着风电在我国能源结构中比重的增大及装机容量的迅速增加，风力发电所具有的随机性、波动性等特点对电网的安全稳定运行带来了巨大挑战，大规模风电并网对电力系统造成了许多不利影响[1].风电功率预测(Wind Power Prediction，WPP)作为一种保证电网安全运行和提高风电使用效益的重要工具，得到了广泛的研究和应用.风电预测误差的大小及预测时间的长短对于电网运行的安全性、经济性有着重要的影响和深远的意义[2-3].

WPP按时间尺度分为中长期、短期和超短期预测.超短期预测有助于在线优化机组组合与经济负荷调度[4].对短期与超短期预测的时效尚缺乏共识，国家电网公司2011年发布的《风电功率预测功能规范》分别规定为次日零时起3 d和未来0～4 h，时间分辨率为15 min.[5]

针对目前的研究现状，本文提出了用粒子群(PSO)算法优化支持向量回归机(SVR)的惩罚因子C、不敏感损失参数ε和核函数参数γ的方法，并根据风电预测的特点在新疆哈密市的一个风电场建立了超短期风电预测模型，引入均方根误差RMSE和复测定系数R2作为模型的评价指标.通过实验结果对比，本文提出的方法显著提高了运算速度和预测精度.

1 算法介绍

1.1 SVR及其参数选取

1995年俄罗斯科学家Vladimir Vapnik[6]首次提出了支持向量机SVM理论，它是一种有监督的学习过程，通常用来进行分类(Support Vector Classification，SVC)及回归预测分析.非线性SVR主要是通过对输入空间进行非线性变换升维后，在高维空间中构造线性决策函数来实现线性回归，从而得到输入空间的非线性回归.升维变换一般通过核函数来实现，核变换后的决策函数为

y=wT·φ(x)+b.

(1)

通过寻找最优w和b，得到最优化问题：

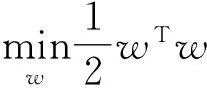
s.t.yi-wT·φ(xi)-b≤ε；

wT·φ(xi)+b-yi≤ε；

i=1，2，…，n.

(2)

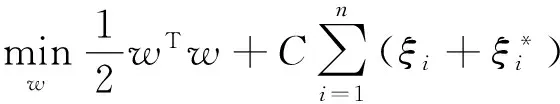
s.t.yi-wT·φ(xi)-b≤ε+ξi；

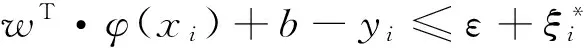
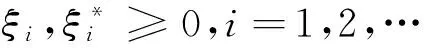
(3)

利用拉格朗日乘子，(3)式可以转化为：

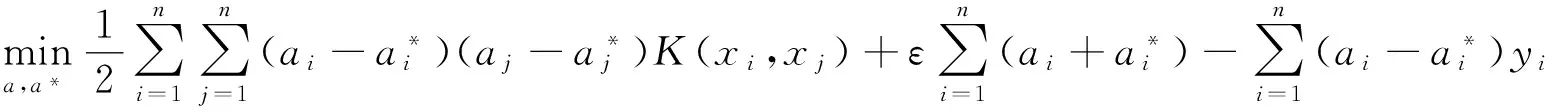
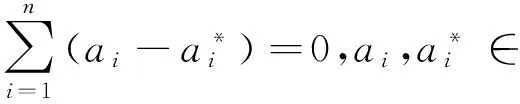
(4)

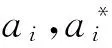
k(xi，xj)=e-γ‖xi-xj‖2.

(5)

式中γ>0是RBF的核函数参数.

1.2 PSO对SVR参数的优化

由(4)和(5)式可知，C，ε和γ是影响SVR性能的关键因素.在风电预测的实践过程中发现，C，ε和γ3个参数中ε的取值在某种程度上独立于C和γ的选取，因此可以根据SVR建模的精度要求先确定ε，然后再用粒子群算法优化参数C和γ.

PSO算法是1995年J.Kennedy博士模拟鸟群的捕食行为提出的一种高效、多维、并行的寻优算法[10].本文采用PSO算法建立位置、速度搜索模型来寻找最优参数(C，γ)组合.设群体中的每个粒子由二维向量(C，γ)组成，第i个粒子在二维解空间的位置ui=(ui1，ui2)T，其速度vi=(vi1，vi2)T.本次迭代的个体极值为p，全局极值为g.在每次迭代中，粒子跟踪个体极值、全局极值和自己前一次迭代的状态来调整本次迭代的位置和速度，迭代公式为：

vi(t+1)=ωvi(t)+c1r1(p-ui(t))+c2r2(gi-ui(t))；

(6)

ui(t+1)=ui(t)+vi(t+1).

(7)

其中：vi(t)，vi(t+1)，ui(t)，ui(t+1)分别是第i个粒子在本次和下一次迭代的速度和位置；c1，c2是学习因子，其初始值本文分别取1.5和1.7；r1，r2是[0，1]之间的随机数；ω是权重因子，为加快收敛速度，其值应随算法的进行根据(8)式自动调节，即

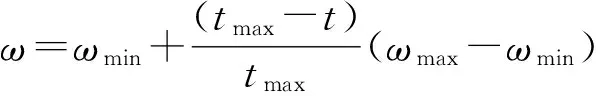
(8)

其中：ωmax，ωmin∈[0，1]分别为最大和最小权重因子，t为当前迭代次数，tmax为总迭代次数.

1.3 预测模型的评价指标

为了反映SVR建模的回归性能，本文引入均方根误差和复测定系数作为模型的评价指标.均方根误差(RMSE)的计算公式为

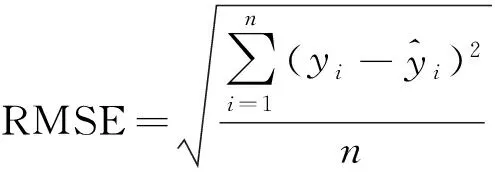
(9)

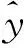
复测定系数的计算公式为

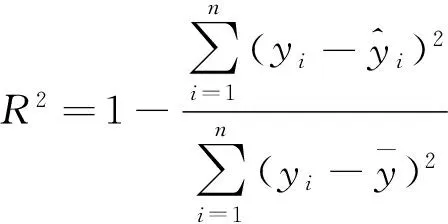
(10)

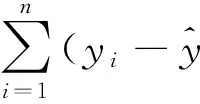
2 风电场物理建模及数据处理

根据预测物理量的不同，风电功率预测方法可以分为2类：第1类是先对风速进行预测，然后根据风电机组或风电场的功率曲线得到风电场输出功率；第 2 类为直接预测风电场的输出功率.

风电功率依赖于风电场的地理环境(包括地形地貌、粗糙度、塔影及尾流效应等)与气象条件(包括风速、风向、气 压 及 温 度 等).本文主要以风电场的气象条件为基础，在已有气象数据的前提下预测未来超短期的气象条件，为在线优化机组组合与经济负荷调度提供技术支持.

2.1 影响风电出力的因素

风力机捕获的风功率[12-13]可表示为

P=CpAρv3/2.

(11)

其中：P为风机输出功率，单位为kW；Cp为风轮的功率系数；ρ为空气密度，单位为kg/m3；A为风轮扫掠面积，单位为m2；v为风速，单位为m/s.

由(11)式可知，影响风力机出力的重要因素是ρ和v，其中v是关键因素.ρ和温度、湿度及大气压强密切相关，因此在WPP中还应该考虑以上因素.

2.2 风电场物理建模

为了验证本文提出的预测算法的可行性，以新疆哈密市巴里坤县三塘湖乡风电场(坐标：N为44°06.742′，E为92°54.901′，海拔为1 434 m，地形为山地)中测风塔的监测数据作为预测模型的训练和测试样本集.考虑到2.1节所述的影响因素，构成样本向量为

y=(v90avg，v90max，v90min，v80avg，v80max，v80min，v70avg，v70max，v70min，

a90avg，a70avg，a10avg，Tavg，Tmax，Tmin，Pavg，t).

(12)

其中：t为采样时刻点(每10 min采样一次)；v90avg，v90max，v90min为测风塔90 m高处的平均、最大和最小风速；v80avg，v80max，v80min为测风塔80 m高处的平均、最大和最小风速；v70avg，v70max，v70min为测风塔70 m高处的平均、最大和最小风速；a90avg，a70avg，a10avg为测风塔90，70，10 m高处风向的平均值；Tavg，Tmax，Tmin为温度的平均、最大和最小值；Pavg为大气压强均值.

2.3 数据的选取和预处理

在选取训练和测试数据时，存在相似日和相邻日的问题.相似日是指一个季度中，与预测日具有相同天气类型的历史日，而相邻日是指位于预测日之前，且相连的历史日[14-15].相似日能有效地反映风电出力的趋势，而相邻日数据可弥补仅以天气条件作为依据进行预测的不足.

2.2节所述风电场每10 min采样1次，每天会产生144组数据，以2015年2月1日至5日的720组相邻日数据作为训练样本，2015年2月6日的144组数据作为测试样本.样本选定后用

(13)

对每组数据的各个分量进行归一化预处理，将所有数据均归一化到[-1，1]的范围内.(13)式中：yi(j)为分量，yimax(j)和yimin(j)分别为第j个分量的最大和最小值，xi(j)为归一化后的分量，i=1，2，…，n(n为样本数)，j=1，2，…，17.

3 实例预测及结果分析

将2.3节中经过归一化后的训练样本集的第一列向量xi(1)作为SVR的训练目标输出样本，xi(2，…，17)作为SVR的训练输入样本.首先用PSO算法寻优参数C，ε，γ，得到的最优参数分别为C=22.484 7，ε=0.010 0，γ=0.010 0.然后用该训练样本训练SVR进而建立风电预测的SVR预测模型，最后用测试样本得到预测结果并将此结果与该风电场的实测运行数据做对比(对比结果如图1所示)，采用RMSE和复测定系数R2评价预测模型的精确度.

为了验证本文提出算法(PSO-SVR)的优越性，与遗传算法优化支持向量机模型(GA-SVR)做比较(GA优化的参数为C=11.492 4，ε=0.046 7，γ=0.010 4)，比较结果见表1.从表1可以看出，PSO-SVR 预测模型的RMSE比GA-SVR低约 2.3%，复测定系数R2比GA-SVR高约0.01，预测时间缩短了约47%，这说明本文提出的算法有较高的预测精度和运算速度，其学习能力和泛化能力也得到了提高.

表1 两种预测方法比较

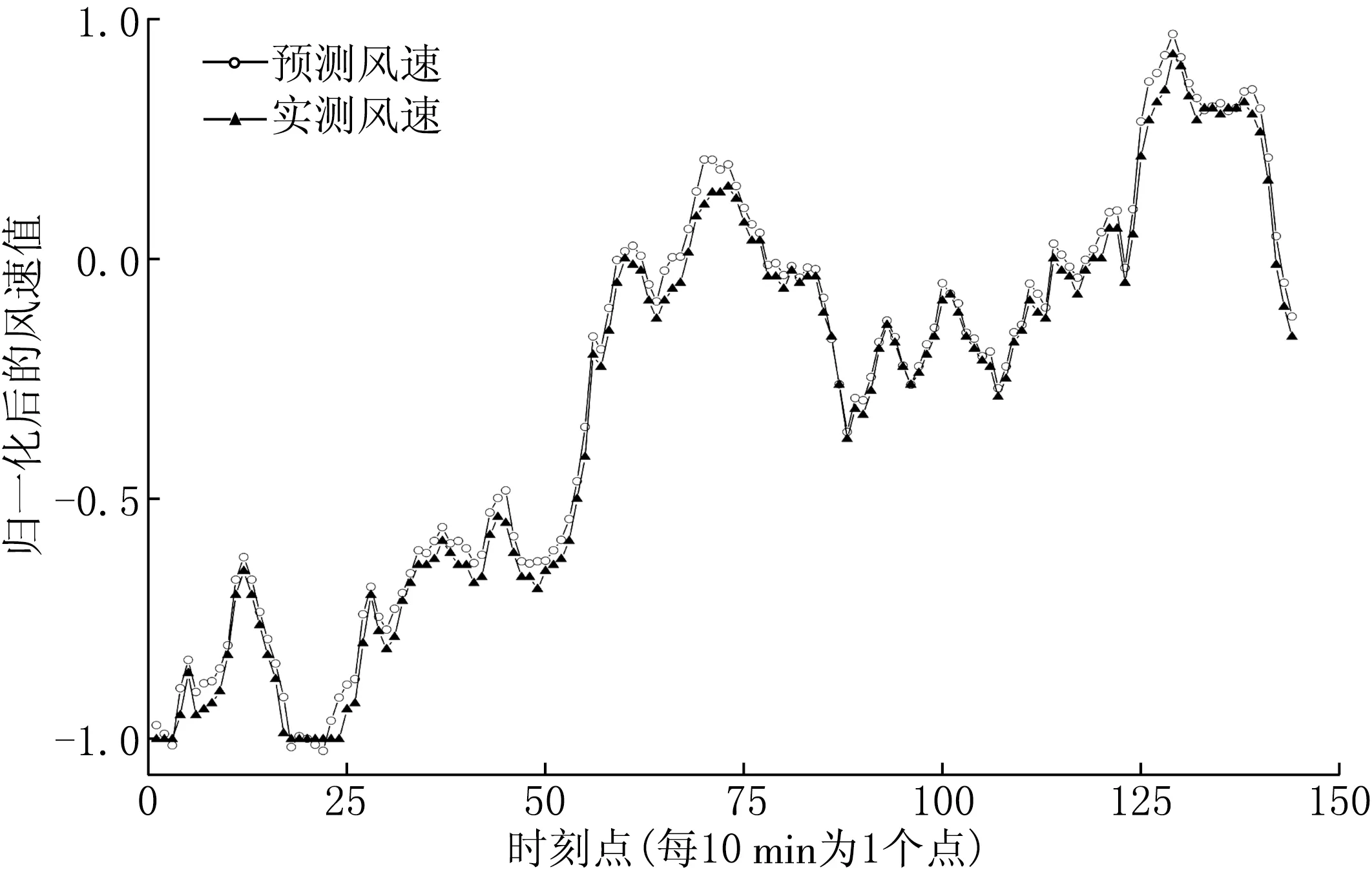
图1 风速预测曲线

4 结论

本文针对风电并网带来的安全稳定和经济运行问题，利用风电场中测风塔的历史风速数据和环境参数作为实验数据构建风电场物理模型，并用粒子群算法优化SVR的惩罚因子C、不敏感损失参数ε和核函数参数γ，提出了PSO-SVR风电功率超短期预测模型.GA-SVR比较，PSO-SVR预测模型的RMSE比GA-SVR低约 2.3%，复测定系数R2比GA-SVR高约0.01，预测时间缩短了约47%，这说明本文提出的预测模型在超短期风电功率预测上有较高的预测精度和运算速度.

[1] 薛禹胜，雷兴，薛峰，等.关于风电不确定性对电力系统影响的评述[J].中国电机工程学报，2014，34(29)：5029-5040.

[2] 王丽婕，冬雷，高爽.基于多位置NWP与主成分分析的风电功率短期预测[J].电工技术学报，2015，30(5)：79-84.

[3] 吴栋梁，王扬，郭创新，等.电力市场环境下考虑风电预测误差的经济调度模型[J].电力系统自动化，2012，36(6)：23-28.

[4] 薛禹胜，郁琛，赵俊华，等.关于短期及超短期风电功率预测的评述[J].电力系统自动化，2015，39(6)：141-151.

[5] 刘纯，裴哲义，王勃，等.风电功率预测功能规范[S].北京：国家电网公司，2011：1-3.

[6] VAPNIK V N.The nature of statistical learning theory[M].New York：Springer，1995：280-292.

[7] HSU C W，LIN C J.A simple decomposition method for support vector machine[J].Machine Learning，2002，46(123)：219-314.

[8] 舒坚，汤津，刘琳岚，等.基于模糊支持向量回归机的WSNs链路质量预测[J].计算机研究与发 展，2015，52(8)：1842-1851.

[9] 黄为勇，王义，田秀玲，张艳华.一种基于SVR的发动机多模式故障诊断方法[J].仪器仪表学报，2015，36(9)：2112-2119.

[10] 朱永红，丁恩杰，胡延军.PSO优化的能耗均衡WSNs路由算法[J].仪器仪表学报，2015，36(1)：78-86.

[11] RATNAWEERA A，HALGAMUGE S，WATSON H C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J].IEEE Transactions on Evolutionary Computation，2004，8(3)：240-255.

[12] 岳有军，徐玥，赵辉，等.基于云模型的独立变桨距控制仿真研究[J].化工自动化及仪表，2014，41(5)：481-485.

[13] 秦斌，姜学想，周浩，等.基于SVM的永磁直驱风电系统滑模变桨距控制[J].仪器仪表学报，2014，35(7)：1525-1531.

[14] 丁明，刘志，毕锐，等.基于灰色系统校正-小波神经网络的光伏功率预测[J].电网技术，2015，39(9)：2438-2443.

[15] 任金霞，游鑫，余志武.电力系统短期电力负荷预测仿真研究[J].计算机仿真，2015，32(5)：132-135.

(责任编辑：石绍庆)

Ultra-short-term wind power forecasting based on svr optimized by particle swarm optimization

XU Wei-jun1，PEI Huan2，WEI Yong2

(1.Department of Electrical and Information Engineering，Northeast Petroleum University at Qinhuangdao，Qinhuangdao 066004，China； 2.College of Information Science and Engineering，Yanshan University，Qinhuangdao 066004，China)

Establishing the wind power prediction system and improving the accuracy and speed of prediction is one of the key technology for large-scale development of wind power.Analyzing the main factors influencing the fan output and combining the measured wind speed data with wind farms environmental parameters，this paper proposes a wind power ultra-short-term forecast model based on SVR optimized by particle swarm optimization.The model can effectively optimize the main parameters of SVR.Compared with GA-SVR，the model has higher prediction precision and computing speed on the ultra-short-term wind power prediction.

wind power；ultra-short-term prediction；support vector regression machine(SVR)；particle swarm optimization algorithm

1000-1832(2017)01-0073-05

10.16163/j.cnki.22-1123/n.2017.01.014

2016-03-01

河北省自然科学基金资助项目(D2014203218)；燕山大学青年教师自主研究计划项目(15LGBO22).

徐炜君(1981—)，男，硕士，主要从事风力发电系统及其控制研究.

TM 715 [学科代码] 480·80

A