基于BiCR算法的数值保角变换计算法

吕毅斌，代荣恒，王樱子

(1.昆明理工大学理学院，云南 昆明 650500；2.昆明理工大学计算中心，云南 昆明 650500)

基于BiCR算法的数值保角变换计算法

吕毅斌1，代荣恒1，王樱子2

(1.昆明理工大学理学院，云南 昆明 650500；2.昆明理工大学计算中心，云南 昆明 650500)

将BiCR(Bi-Conjugate Residual)算法与基于模拟电荷法的外部数值保角变换算法原理相结合，提出了基于BiCR算法的数值保角变换计算法，并通过数值实验检验了所提出算法是有效且可行的.

模拟电荷法；保角变换；BiCR算法

保角变换是函数论的一个基本问题，它被广泛应用于电磁理论、弹性理论、热传输、流体力学与图像处理等许多物理学和工学的问题上.[1-3]解析法和数值计算法是保角变换的主要求解方法.在保角变换中黎曼存在定理可以证明保角变换是构造型的变换，因此通常只能知道变换函数存在但不能求出，只有很少数情况下才能用初等函数表示解析函数.在复杂的实际应用工程问题中，很多情况只能通过数值方法来近似求解满足给定条件的保角变换.

基于模拟电荷法的数值保角变换算法由日本学者天野要提出.[4-6]相对于传统的级数展开法、积分方程法与变分法等数值保角变换求解方法，利用模拟电荷法原理计算保角变换的过程中不计算数值积分，所以计算时间短.在保角变换的计算中可以使用拉普拉斯方程的最大值原理评价误差，因而保角变换的计算精度很高.

BiCR算法[7-8]由Sogabe提出，是CR(Conjugate Residual)方法的推广，是一种可以高效求解线性方程组的算法，主要用于求解非对称线性方程组.

本文首先配置模拟电荷点和边界上的约束点，进而得到约束方程.然后通过BiCR算法求解约束方程，在求解出保角变换半径的近似值和模拟电荷的电荷量后，构造保角变换的近似函数.最后通过数值实验对算法进行了检验.

1 基于模拟电荷法的外部数值保角变换算法

本节简要介绍基于模拟电荷法的外部数值保角变换算法[9-11].考虑如下保角变换：设D为z平面上任意封闭若尔当曲线C的外部区域，此时存在一个保角变换函数f(z)，将区域D映射为w平面上的单位圆的外部区域|w|≥1.在不失一般性的情况下，假定原点z=0在C的内部且有f(0)=0.此时，若f(z)满足正规化条件f(∞)=∞，f′(∞)>0，则f(z)可以唯一表示为

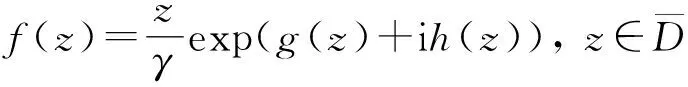
其中：g(z)是Dirichlet问题

的解.γ是外部变换半径.h(z)为g(z)在D内的共轭调和函数，且有h(∞)=0.此时由模拟电荷法，可用C围成区域内部配置的N个电荷点ζj作为极的对数势场的一维结合

来高精度的近似g(z)，这时h(z)可以用如下函数近似：

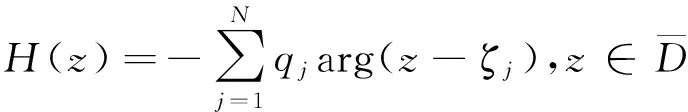
由于电荷qj以及变换半径γ满足Dirichlet问题边界条件

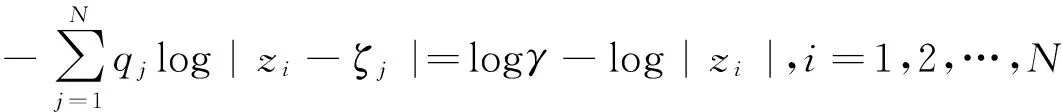
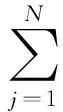
其中Γ为外部变换半径γ的近似.从而只需求解以上线性方程组并回带，即可得到数值保角变换函数f(z).

综上，基于模拟电荷法的外部数值保角变换算法步骤如下：

(1) 分配适当数量的约束点和模拟电荷点，安排相对应的约束点和模拟电荷点的位置；

(2) 利用Dirichlet问题边界条件构造线性方程组，得到保角变换半径和电荷量；

(3) 通过保角变换半径和电荷量构造外部保角变换近似函数.

2 基于BiCR算法的外部数值保角变换新算法

在前节阐述的基于模拟电荷法的数值保角变换算法过程中，线性方程组的求解对最终计算结果起着关键性作用.经整理，需要求解的线性方程组为

Ax=b(A∈R(N+1)×(N+1)，b∈RN+1).

其中

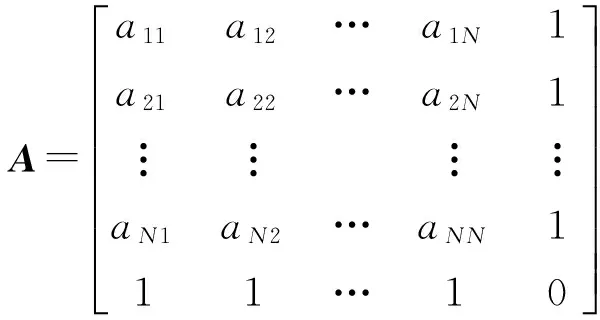
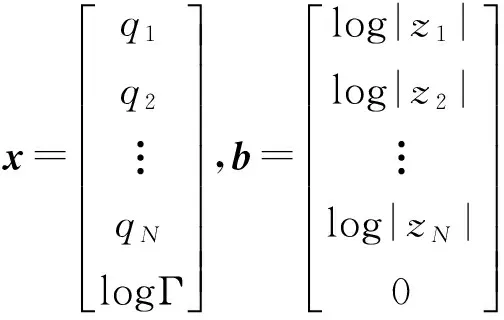
这里aij=log|zi-ζj|.

本文采用BiCR算法对以上线性方程组进行求解.[12-14]BiCR算法是一种适用于非对称线性方程组的迭代求解方法，用零向量作为初始解.下面给出标准的BiCR算法步骤：

Input：A，b，x0.

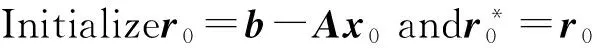
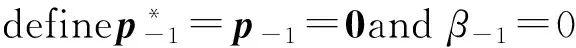
forn=0，1，…，

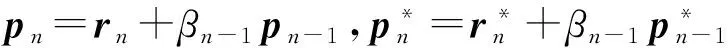
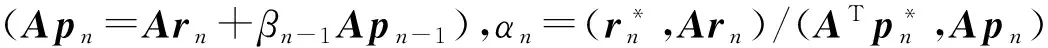
xn+1=xn+αnpn，rn+1=rn-αnApn，

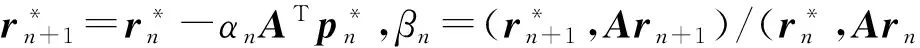
end.

在上述BiCR算法中，x0是给定的初始近似解，这里选取零向量；r0=b-Ax0为初始向量.

3 数值实验

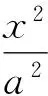
在下面的数值例中，选取了两种不同的参数a进行实验.外部数值保角变换的误差是根据拉普拉斯方程的最大值原理进行评价.将误差定义为z平面上椭圆边界上的点保角变换到w平面上的相应点与单位圆周的最大距离，即误差计算公式为error=max{‖f(z)|-1|}.

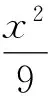
根据天野要[4]的方法对模拟电荷点和约束点的位置进行了设置，模拟电荷点数量为200.椭圆边界及其边界外部区域情况见图1，保角映射的结果见图2，保角映射的最终误差值为7.147 6×10-8.本实验通过给定不同的约束点和模拟电荷点得到误差分布曲线见图3.

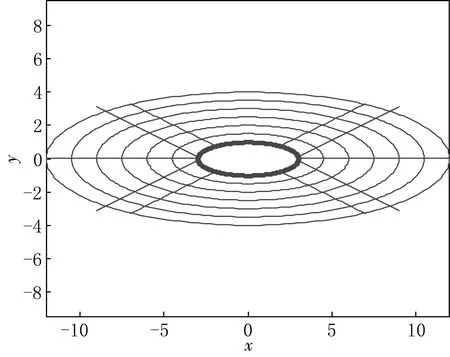
图1 a=3时椭圆及外部区域

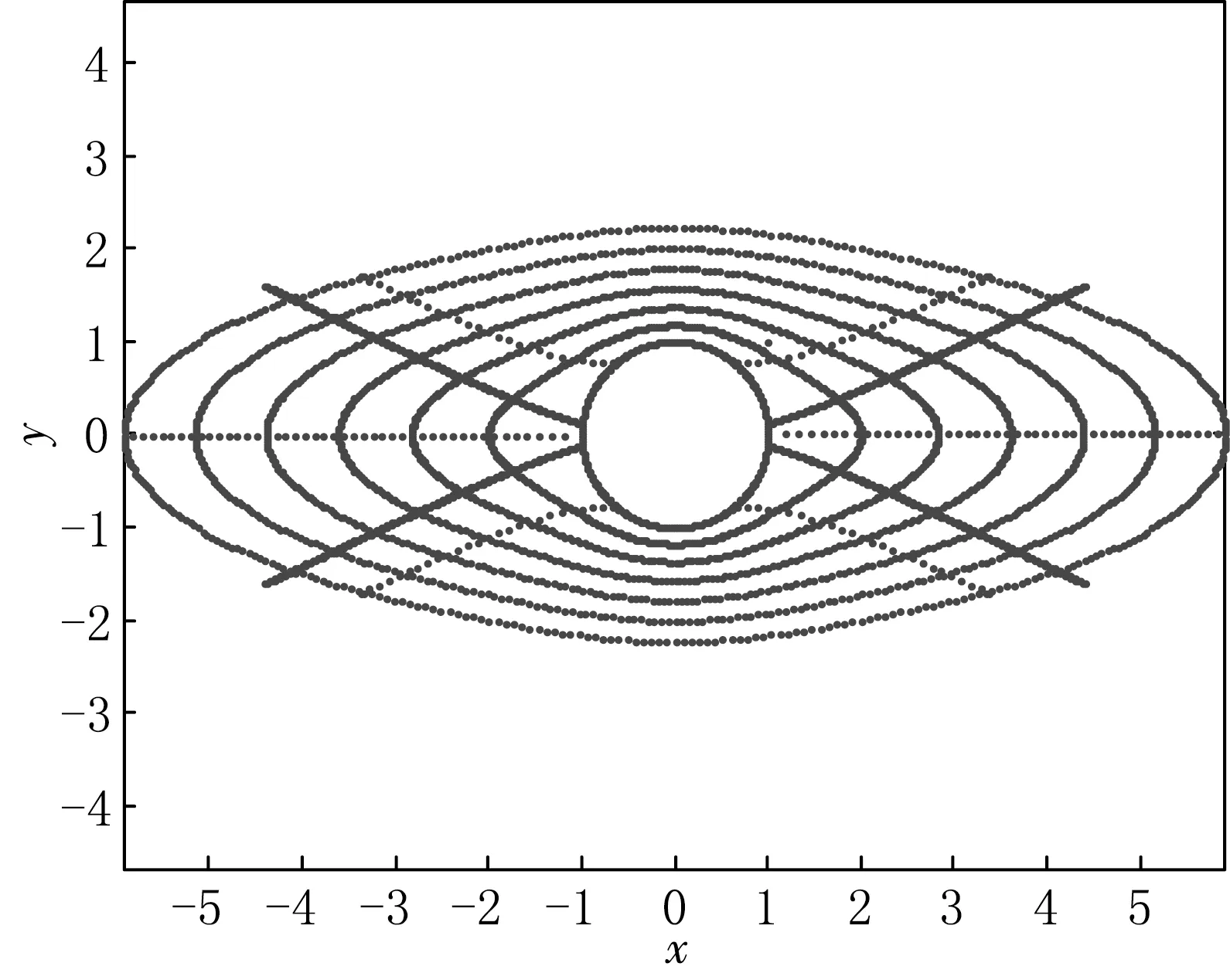
图2 a=3时椭圆及外部区域的保角变换

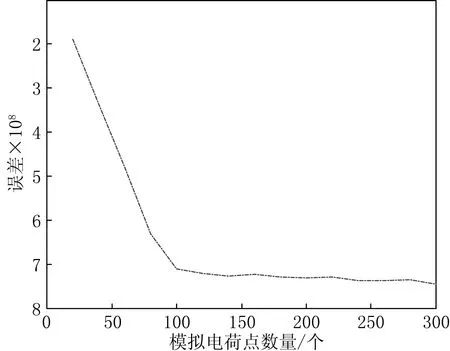
图3 a=3时数值保角变换的误差分布曲线

例2 对a=5时的椭圆边界及其边界外部的区域进行保角变换，椭圆边界为

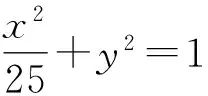
与例1相同，根据天野要[4]的方法对模拟电荷点和约束点的位置进行了设置，模拟电荷点数量取为200，椭圆边界及其边界外部区域情况见图4，保角映射的结果见图5，保角映射的最终误差值为5.713 8×10-8.本实验通过给定不同的约束点和模拟电荷点得到误差分布曲线见图6.

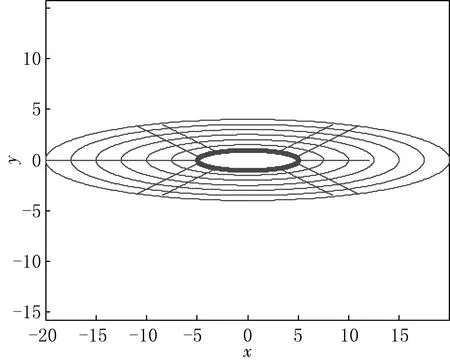
图4 a=5时椭圆及外部区域

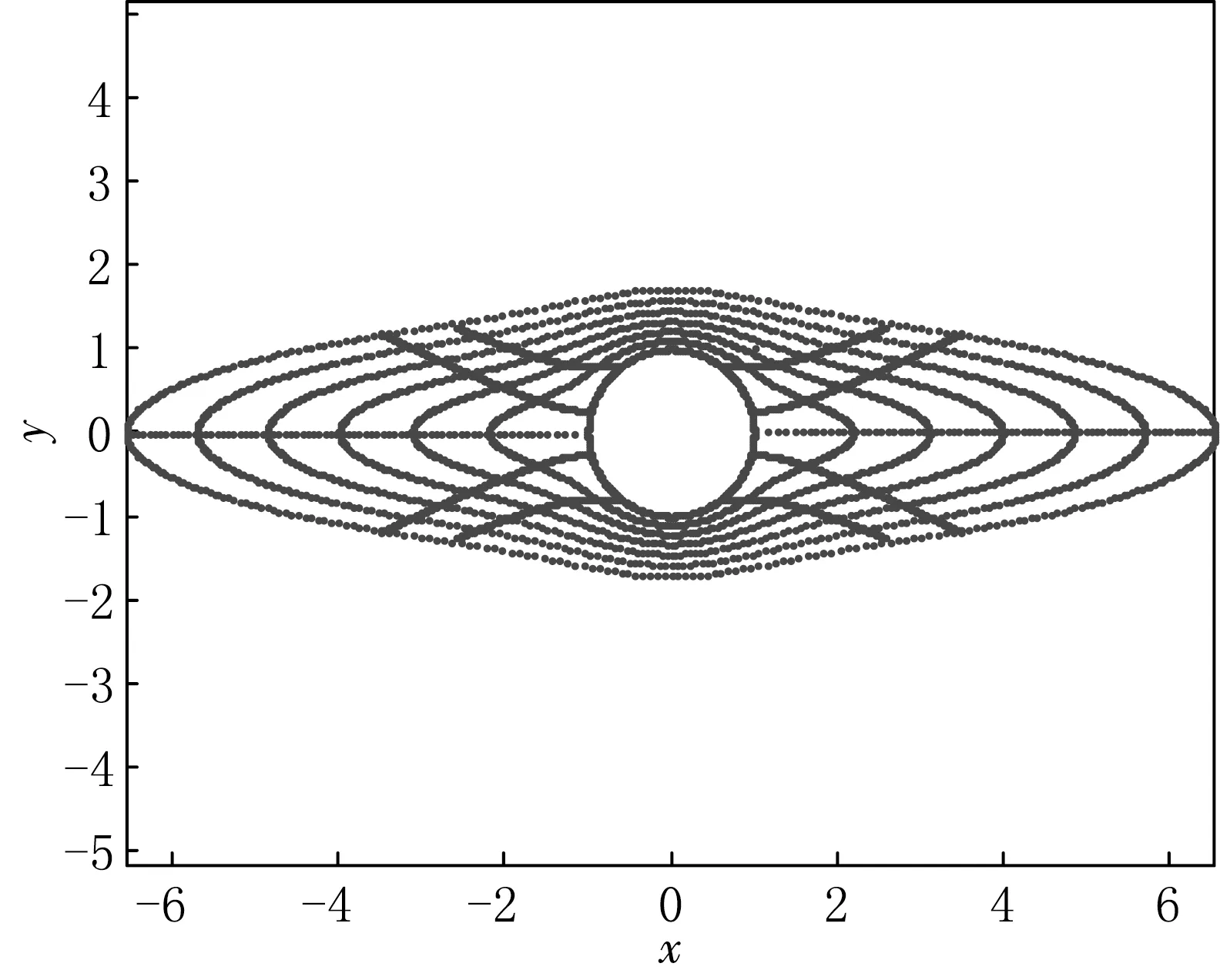
图5 a=5时椭圆及外部区域的保角变换

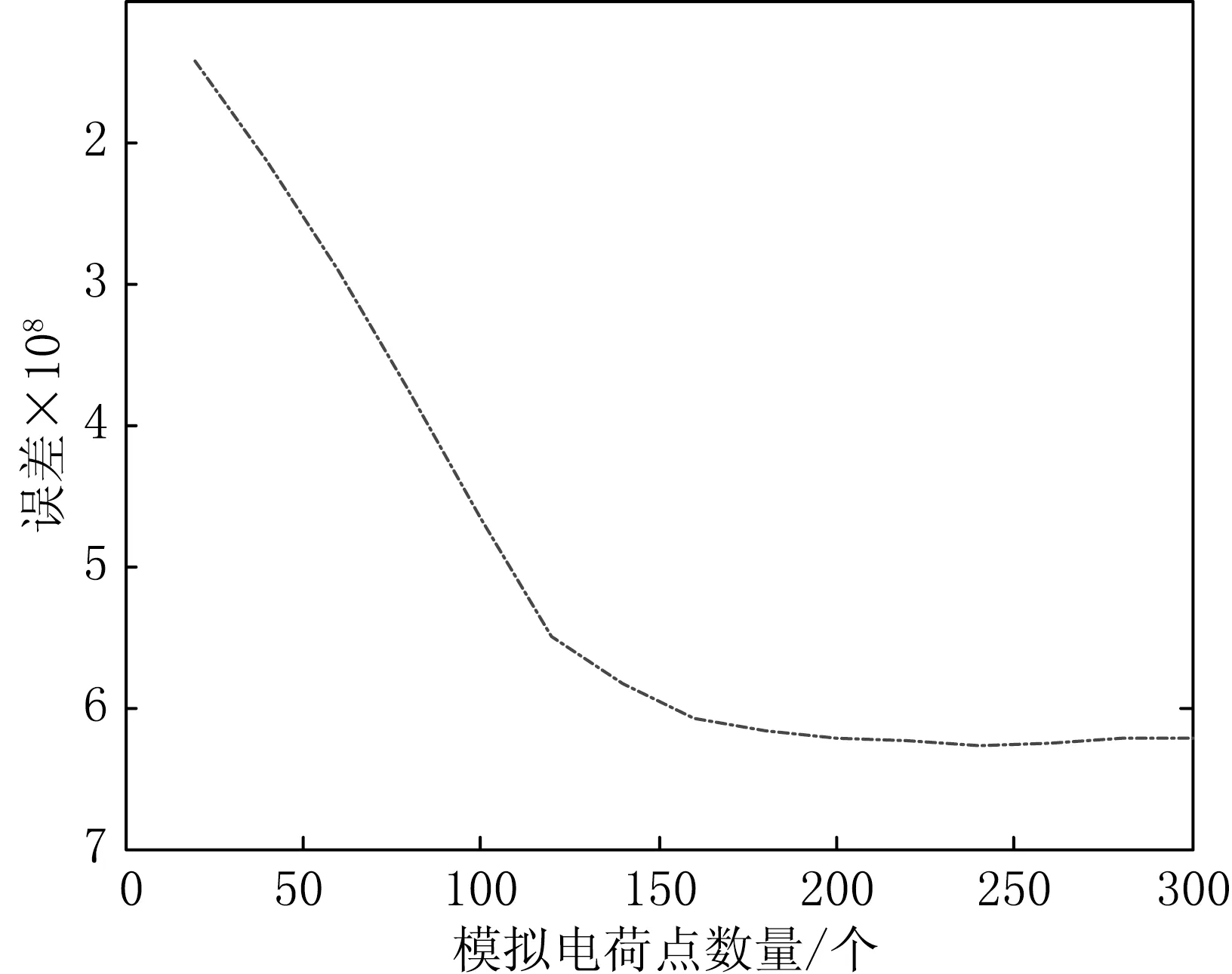
图6 a=5时数值保角变换的误差分布曲线

上述实验表明，本文阐述的算法可以高精度的构建保角变换函数，故而该算法是行之有效的，并且通过参数的调整，可以得到更好的结果.

4 结论

本文将求解非对称线性方程组的BiCR算法与基于模拟电荷法的数值保角变换算法相结合，提出了数值保角变换的一个新算法，并通过数值实验，检验了算法的有效性.这个算法具有程序简洁、运行占用内存小、计算精度高等优点.在对其进行误差分析后，可以将其应用于多连通区域保角变换和流体力学等很多物理学和工学问题中.

[1] 曹伟杰.保形变换理论及其应用[M].上海：上海科技文献出版社，1988：193-231.

[2] 徐趁肖，朱衡君，齐红元.复杂边界单连通域共形映射解析建模研究[J].工程数学学报，2002(4)：135-138.

[3] 朱满座.数值保角变换及其在电磁理论中的应用[D].西安电子科技大学，2008.

[4] AMANO K.Numerical conformal mapping based on the charge simulation method[J].Trans Inform Process Soc Japan，1987，28：697-704.

[5] AMANO K.Numerical conformal mapping of exterior domains based on the charge simulation method[J].Trans Inform Process Soc Japan，1988，29：62-72.

[6] AMANO K.A charge simulation method for the numerical conformal mapping of interior，exterior and doubly-connected domains[J].Comput Appl Math，1994，53：353-370.

[7] SOGABE T，SUGIHARA M，ZHANG S L.An extension of the conjugate residual method to non-symmetric linear systems[J].Journal of Computational and Applied Mathematics，2009，226：103-113.

[8] SOGABE T，ZHANG S L.Extended conjugate residual methods for solving nonsymmetric linear systems[M].New York：Science Press，2003：88-99.

[9] LU Y B，WU D A，WANG Y Z，et al.The accuracy improvement of numerical conformal mapping using the modified Gram-Schmidt method[M].Berlin：Springer，2013：555-563.

[10] SAKURAI T，SUGIURA H.A method for numerical conformal mapping by using Pade approximations[J].Trans Inform Process Soc Japan，2002，43：2959-2962.

[11] 姚国梅，吕毅斌，王樱子.数值保角变换的新算法[J].价值工程，2014，31：308-310.

[12] 杨志梅.解非对称线性系统的混合BiCR法[D].广西大学，2010.

[13] 左宪禹，谷同祥，莫则尧，等.适合于分布式并行计算的一种并行广义乘积型双共轭残差方法[J].应用数学与计算数学学报，2013(2)：246-259.

[14] 仲妍，骆志刚，吴枫.求解非对称线性方程组的s-BiCR算法[J].国防科技大学学报，2010(2)：61-67.

(责任编辑：李亚军)

The BiCR method for numerical conformal mapping

LU Yi-bin1，DAI Rong-heng1，WANG Ying-zi2

(1.Faculty of science， Kunming university of science and technology， Kunming 650050， China； 2.Computer Center， Kunming university of science and technology， Kunming 650050， China)

A new method for numerical conformal mapping is considered.In this method，the linear equation of charge simulation method is solved using the BiCR(Bi-Conjugate Residual) algorithm，and the approximate conformal mapping function is constructed using the charge points and conformal mapping radius.Finally，the efficiency of the proposed method is illustrated by several numerical examples.

charge simulation method；numerical conformal mapping；BiCR method

1000-1832(2017)01-0048-05

10.16163/j.cnki.22-1123/n.2017.01.010

2015-08-21

国家自然科学基金资助项目(11461037).

吕毅斌(1972—)，男，博士，副教授，主要从事科学计算与图像处理研究；通信作者：王樱子(1972—)，女，硕士，讲师，主要从事科学计算与数学应用软件设计研究.

O 241.2 [学科代码] 110·61

A