基于矩生成函数的多元响应降维子空间估计

甘胜进，游文杰

(福建师范大学福清分校电子与信息工程学院，福建 福清 350300)

基于矩生成函数的多元响应降维子空间估计

甘胜进，游文杰

(福建师范大学福清分校电子与信息工程学院，福建 福清 350300)

提出一类新的估计多元响应降维子空间方法，即基于矩生成函数(GF)、绝对值矩生成函数(G-A)与矩生成函数海塞主方向方法(G-PHD).给出了该方法估计量的相合性以及渐近性性质，并进行了实例模拟.

充分降维；切片逆回归；矩生成函数；绝对值矩生成函数；海塞主方向

1 预备知识

考虑一维响应变量Y和p维解释变量X=(X1，X2，…，Xp)T之间回归问题的主要目的是研究在X给定的条件下，Y对X的条件分布函数FY|X如何随自变量X变化.如果存在p×k(k≤p)矩阵η(列满秩)满足

Y‖X|X⟺Y‖X|ηTX，

(1)

其中‖表示统计独立，Y‖X|U表示在任意给定U值的情况下，X与Y相互独立，则FY|X(y|x)=FY|ηTX(y|ηTx)，这样X中有关Y的信息就包含在ηTX中，Y对X条件分布的维数是k维，不再是p维.如果k相对于维数p微不足道，那么降维目的就达到了.特别当k=1，2时，便可在概要图上分析Y与X之间的回归关系.Li[1]首次提出切片逆回归(简称SIR)方法，即用X对Y的逆回归均值函数E(X|Y)来估计η.由于Y‖X|ηTX⟺Y‖X|(ηB)TX，其中B为k阶可逆方阵，可见在上式中η与ηB起到作用是一样的，而η与ηB列向量张成子空间是相同的，故考虑span{η}而非η本身，span{η}表示由η列向量张成的子空间.沿用Fisher充分统计量的概念，称span{η}为其充分降维子空间(简称DRS).进一步地，如果满足(1)式的所有η的交集仍然满足(1)式，则称其为中心降维子空间(简称CS)，记为SY|X，rank(SY|X)称为结构维数.CS是最小的充分降维子空间，通常情况下CS总是存在的.如果感兴趣的是E(Y|X)，结合充分降维就产生均值降维子空间[2]概念，即

Y‖E(Y|X)|ηTX.

(2)

类似CS的讨论，若所有满足(2)式的集合的交集仍然满足(2)式，则称之为中心均值降维子空间(简称CMS)，记为SE(Y|X).令Z=Σ-1/2(X-E(X))，则有转换公式SY|X=Σ-1/2SY|Z[3]，其中Σ=D(X)>0.因此下文不妨假定E(X)=0，D(X)=Ip.

估计降维子空间常用到下面两个基本条件：

(1) 线性条件均值：E(X|ηTX)为ηTX线性函数，即E(X|ηTX)=PηX，∀η∈Rp，其中投影阵Pη=η(ηTη)-1ηT.

(2) 常数条件方差：Var(X|ηTX)为非随机矩阵，即Var(X|ηTX)=I-Pη.

满足线性条件均值的是椭圆分布，而满足条件常数方差的是多元正态分布.下文提出基于矩生成函数方法估计多元响应降维子空间，并给出该方法估计量的相合性和渐近性，最后为该方法的蒙特卡罗模拟.

2 多维响应降维子空间

将一维响应推广到多维响应，就会产生多维响应降维子空间与多维响应均值降维子空间，即

Y‖X|ηTX，

(3)

Y‖E(Y|X)|ηTX.

(4)

其中X=(X1，X2，…，Xp)T，Y=(Y1，Y2，…，Yq)T.

一些一维响应降维子空间估计方法可以推广到多维响应降维子空间的估计，例如多元切片逆回归(简记MS)、最小二乘估计(OLS)和海塞主方向(PHD)[4]，其他估计方法可参看文献[5-10].本文受文献[8-9]启发，提出矩生成函数方法(简记GF).

记φ(t)=E(etTYX)，t∈Rq，φ(t)张成子空间记为M，即M=span{φ(t)|t∈Rq}，则M=span{E(φ(T)φ(T)T)}[11]几乎必然成立，其中T是支撑为Rq的q维随机向量.称M为多元响应降维子空间的矩生成函数估计，其理论依据为下面定理.

定理1 在线性条件均值条件下，M⊆SY|X.

证明 注意到(3)式意味着Y|X，Y|ηTX同分布，故tTY|X，tTY|ηTX同分布.由此以及线性条件均值定义，有

φ(t)=E(etTYX)=E(XE(etTY|X))=E(XE(etTY|ηTX))=

E((X|ηTX)E(etTY|ηTX))=E((X|ηTX)etTY)=PηE(etTYX)⊆span(η).

从上述定理证明过程可知，E(etTYX)可看作Y对X向前回归.另一方面，E(etTYX)=E(etTYE(X|Y))⊆span{E(X|Y=y)|y∈ΩY}，其中ΩY为Y样本空间，从而E(etTYX)也可看作X对Y逆回归，因此E(etTYX)可看作向前回归与逆回归的结合.在线性条件均值条件下span{E(X|Y=y)|y∈ΩY}⊆SY|X，但切片逆回归估计效果对切片数量比较敏感，因此如何选择较为合适的切片数量至今仍是一个公开难题，而本方法避免了对响应变量进行切片，只需样本的矩估计.

定理2 当X为p维标准正态分布时，M⊆SY|X.

证明 类似于定理1的证明及Stein引理[12]，

E(etTYX)=E(XE(etTY|X))=E(XE(etTY|ηTX))=

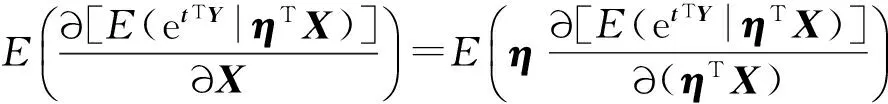
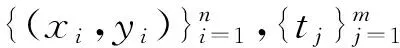
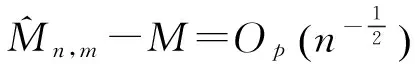
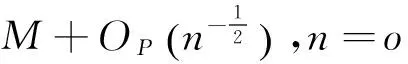
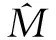
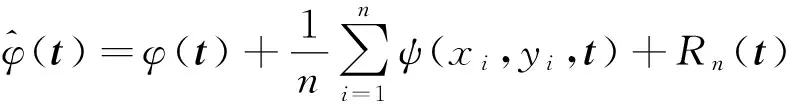
(5)

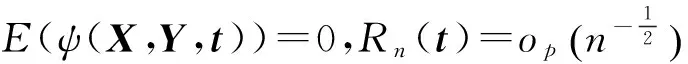
(6)

实际上(5)与(6)式较容易满足.[13]采用类似文献[14]的方法可证明多元渐近正态性.

E(ψ(X，Y，T)φ(T)T|X=xi，Y=yi)}.

证明

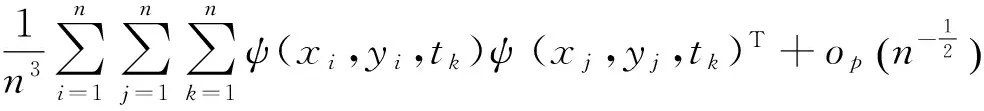
由于E(ψ(X，Y，T)φ(T)T|T=ti)=E(ψ(X，Y，ti))φ(ti)T=0，故两样本U统计量

被下面的投影近似：

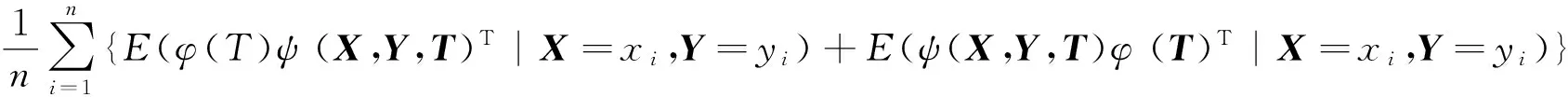
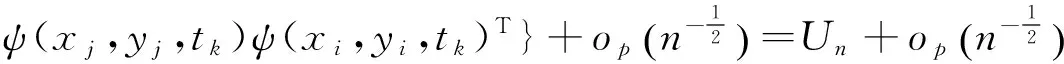
(7)

利用条件期望平滑性和(6)式，可类似上面讨论Un：

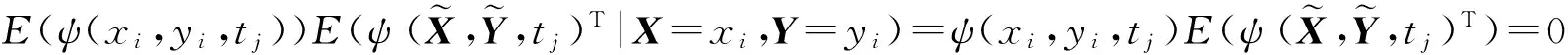
(8)

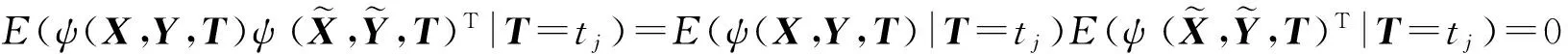
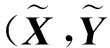
当回归函数是偶函数，并且自变量是对称分布时，多元切片逆回归方法对此类模型失效，可采用两种办法，即绝对值矩生成函数与矩生成海塞主方向，分别简记为G-A、G-PHD.

定理5 在线性条件均值条件下，由φ(t)=E(e|tTY|X)，t∈Rq张成的子空间M⊆SY|X.

此定理证明与定理1类似，故省略.

定理6 当线性条件均值和常数条件方差成立时，由φ(t)=E(etTY(XXT-I))，t∈Rq张成的子空间M⊆SY|X.

证明 由条件期望平滑性，线性条件均值和常数条件方差可得

φ(t)=E(etTY(XXT-I))=E(E(etTY|X)(XXT-I))=

E(E(etTY|ηTX)(XXT-I))=E(etTY(E(XXT|ηTX)-I))=

E(etTY(Var(X|ηTX)+E(X|ηTX)E(X|ηTX)T-I))=PηE(etTY(XXT-I))Pη⊆SY|X.

以上两种方法的样本估计、相合性和渐近性与GF类似，这里不再赘述.

3 数值模拟

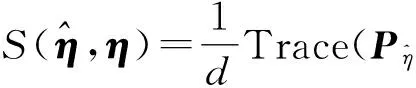
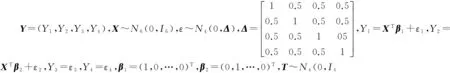
表1为(X，Y)与T的样本容量在某些取值下，采用定理1或定理2中M的样本得到的100次蒙特卡罗随机模拟结果.其中第一列与第一行分别为(X，Y)与T的样本容量n与m的取值，每个表格里第一和第二个数分别表示100次模拟迹相关系数的均值与标准差.

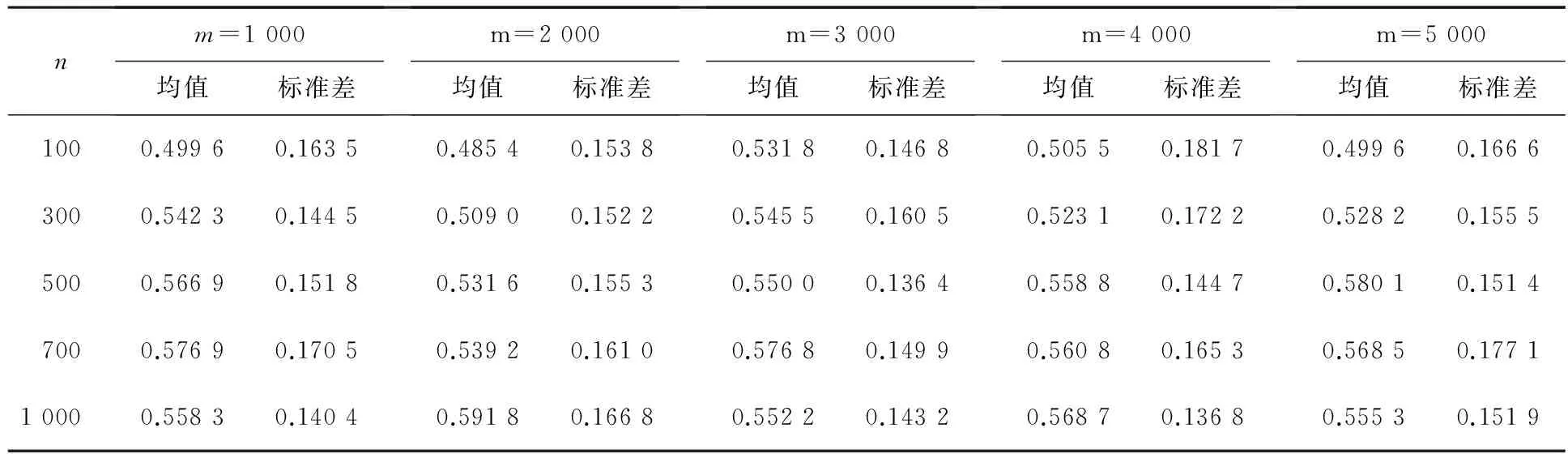
表1 在(X，Y)与T的不同样本容量下100次模拟迹相关系数的均值与标准差

从表1中可以看出，当m固定时，n逐渐变大，估计方向与真实方向接近程度的均值几乎逐渐递增，标准差曲折减少；而当n固定，m逐渐变大时，迹相关系数的均值和标准差变化不大，说明估计效果只依赖于n，印证了定理3的结论.

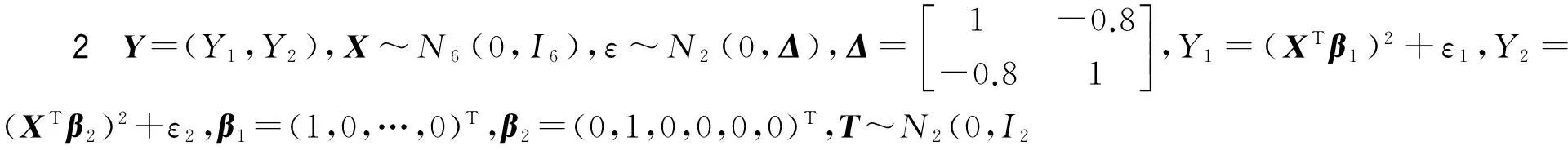
表2为100次重复选取的各个方法在不同样本容量下的估计性能比较，每个格子第一个数为迹相关系数的均值，第二个数为标准差.从中可以看出，GF表现最好，紧随其后的是G-A与G-PHD，但G-A 与GF差别不大.相比之下，OLS和MS(每个响应变量切片数量为4，故总切片数为42=16)表现最差，一个很重要的原因是Y对X回归函数是偶函数.

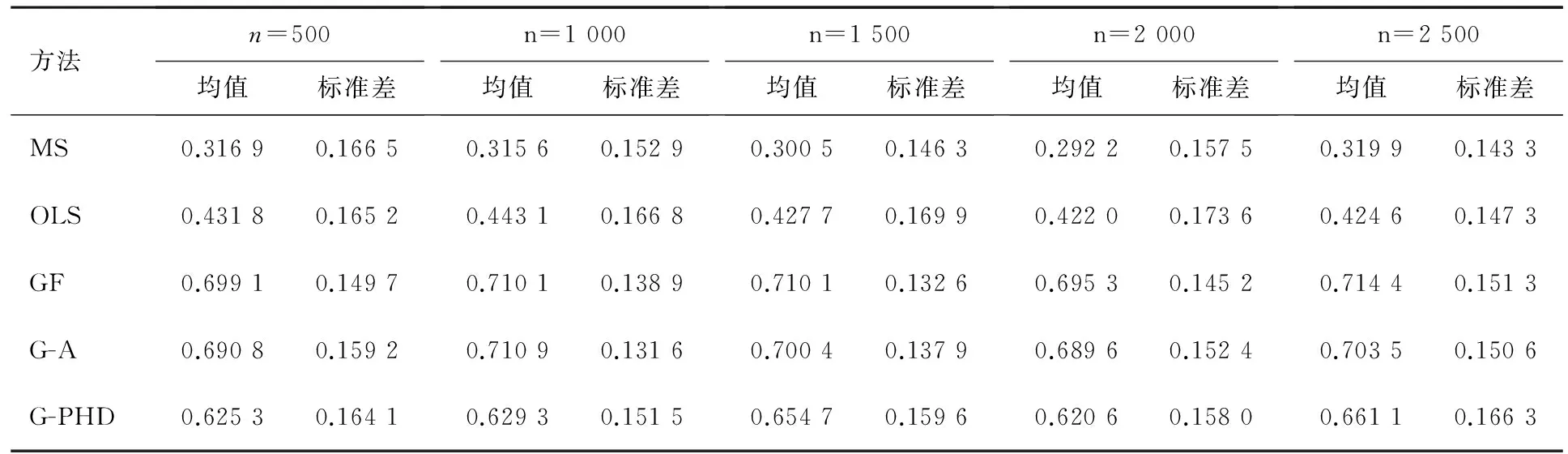
表2 基于模型2的几种选取方法性能比较

图1与图2分别表示100次重复的情况下，三种方法GF，G-A与G-PHD在模型1和模型2上估计效果的箱线图.从中可以看出，对于线性回归函数而言，GF表现是最好的；而对于对称函数来说，GF的估计性能不比其他两种方法差.因此就目前模拟的效果来看，GF具有较好的稳健性，是三种方法中最好的.

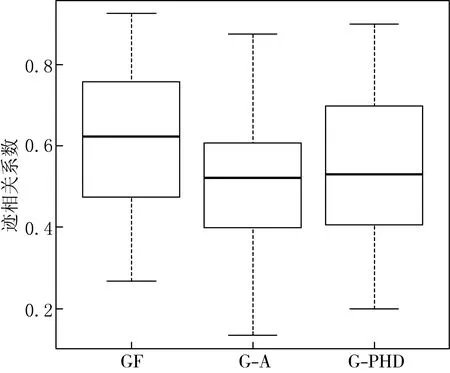
图1n=1 000时模型1中GF，G-A与G-PHD估计效果对比

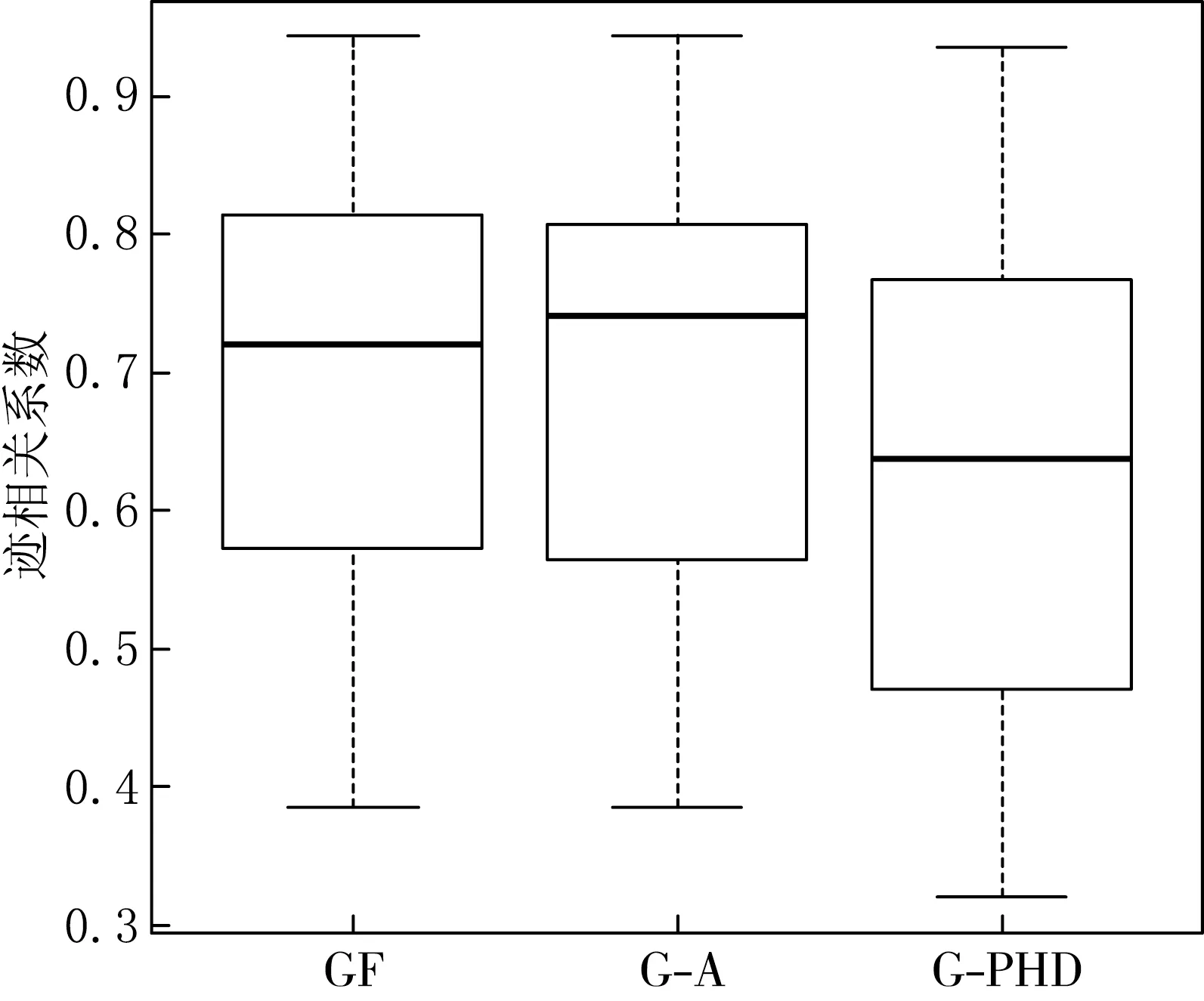
图2n=1 000时模型2中GF，G-A与G-PHD估计效果对比

[1] LI K C.Sliced inverse regression for dimension reduction[J].Journal of American Statistical Association，1991，86：316-327.

[2] COOK R D，LI BING.Dimension reduction for conditional mean in regression[J].The Annals of Statistics，2002，30(2)：455-474.

[3] COOK R D.Regression graphics：ideas for studying regressions through graphics[M].New York：Wiley，1998：104.

[4] YIN XIANGRONG，BURA E.Moment-based dimension reduction for multivariate response[J].Journal of Statistical Planning and Inference，2006，136：3675-3688.

[5] SETODJI C M，COOK R D.K-means inverse regression[J].American Statistical Association and American Society for Quality，2004，46(4)：421-429.

[6] LI B，WEN S Q，ZHU L X.On a projective resampling method for dimension reduction with multivariate responses[J].Journal of American Statistical Association，2008，103：1177-1186.

[7] LI KER-CHAU，ARAGON YVE，SHEDDEN KERBY，et al.Dimension reduction for multivariate response data[J].Journal of American Statistical Association，2003，98：99-109.

[8] ZHU YU，ZENG PENG.Fourier methods for estimating the central subspace and the central mean subspace in regression[J].Journal of American Statistical Association，2006，101：1638-1651.

[9] ZHU LI PING，ZHU LI XING，WEN SONG QIAO.On dimension reduction in regression with multivariate responses[J].Statistica Sinica，2010，20：1291-1307.

[10] LUE H H.On principal Hessian directions for multivariate response regressions[J].Computational Statistics，2010，25(4)：619-632.

[11] YIN X R，COOK R D.Estimating central subspaces via inverse third moments[J].Biometrika，2003，90：113-125.

[12] STEIN C M.Estimation of the mean of a multivariate normal distribution[J].The Annals of Statistics，1981，9：1135-1151.

[13] BICKEL KLAASSEN，RITOV WELLNER.Efficient and adaptive inference in semi-parametric models[M].Baltimore：John Hopkins University Press，1993：19.

[14] ZHU L P，WANG T，ZHU L X.Sufficient dimension reduction through discretization-expectation estimation[J].Biometrika，2010，97(2)：295-304.

[15] FERR L.Determining the dimension in sliced inverse regression and related methods[J].Journal of American Statistical Association，1998，93：132-140.

(责任编辑：李亚军)

Estimate of dimension reduction subspace for multivariate responses based on moment-generating function

GAN Sheng-jin，YOU Wen-jie

(School of Electronic and Information Engineering，Fuqing Branch of Fujian Normal University，Fuqing 350300；China)

A new class of estimators for dimension reduction subspace with multivariate responses are proposed based on some related literature，which are termed as moment-generating function(GF)，absolute moment-generating function(G-A) and moment-generating function of principal Hessian directions(G-PHD) respectively.Consistency and asymptotic property of estimators are given.

sufficient dimension reduction；sliced inverse regression；moment generating function；absolute moment generating function；principal Hessian directions

1000-1832(2017)01-0043-05

10.16163/j.cnki.22-1123/n.2017.01.009

2015-10-29

国家自然科学基金资助项目(61473329)；福建省自然科学基金资助项目(2015J01009)；福建省中青年教师教育科研项目(JAT160566).

甘胜进，男，硕士，讲师，主要从事高维数据充分降维研究；游文杰，男，博士，教授，主要从事统计计算以及数据挖掘研究.

O 213 [学科代码] 110·71

A