利用空间向量探讨几何体中点的存在性问题
■河北省临城中学2014级02班 孙奇士
利用空间向量探讨几何体中点的存在性问题
■河北省临城中学2014级02班 孙奇士
在立体几何中,经常遇到点的存在性问题,即探讨线线平行(垂直),线面平行(垂直)和面面平行(垂直)中的点是否存在。这类问题用空间向量的坐标运算来处理比较简单直观。
一、直线上点的存在
如图1,在侧棱与底面垂直的三棱柱ABC-A1B1C1中,AC= 3,BC=4,AB=5, AA1=4。
(1)求证:AC⊥BC1。
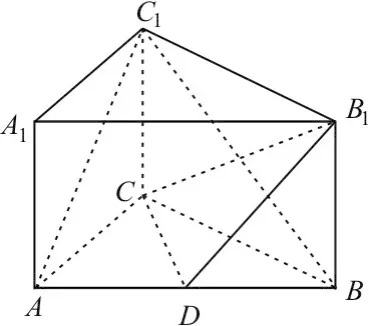
图1
(2)在AB上是否存在点D,使得AC1⊥CD?
(3)在AB上是否存在点D,使得AC1∥平面CDB1。
解析:三棱柱ABC-A1B1C1中,AC=3, BC=4,AB=5,AC,BC,CC1两两垂直。以为C坐标原点,直线CA,CB,CC1分别为x轴,y轴,z轴,建立如图2的空间直角坐标系,则C(0,0,0), A(3,0,0),C1(0,0, 4),B(0,4,0),B1(0, 4,4)。
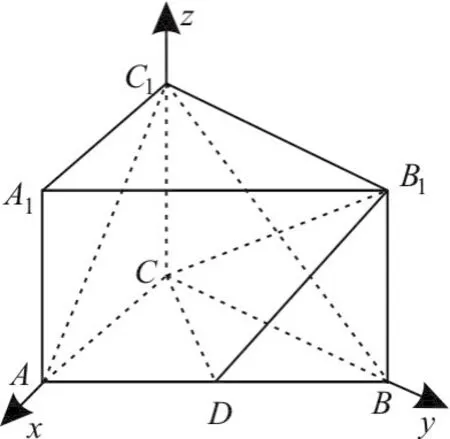
图2
(2)假设AB在上存在点D,使得AC1⊥ CD,则=(-3λ,4λ,0),其中0≤ λ≤1,则D点坐标为(3-3λ,4λ,0)。
所以在AB上存在点D使得AC1⊥CD,此时点D与点B重合。
(3)假设在AB上存在点D使得AC1∥平面CDB1,则=(-3λ,4λ,0),其中0≤λ≤1,D的坐标为(3-3λ,4λ,0)=(3 -3λ,4λ-4,-4)。
此时m(3-3λ)=-3,m(4λ-4)-4n= 0,-4m-4n=4,解得
所以在AB上存在点D使得AC1∥平面CDB1,此时D为AB的中点。
点评:解存在性问题,一般是假设存在,设点的坐标为(x,y,z),再利用点在直线上,将x,y,z用λ表示,根据平行或垂直的数量积运算得到关于λ的方程求解。
二、平面内点的存在
如图3,在四棱锥P-ABCD中, PD⊥底面ABCD,底面ABCD为正方形,PD =DC,E、F分别是AB、PB的中点。
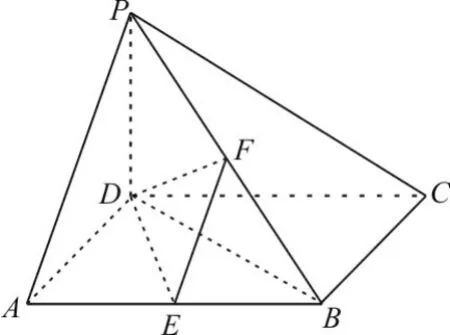
图3
(1)求证:EF⊥CD。
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论。
解析:以DA,DC,DP所在直线分别为轴,y轴,z轴建立如图4所示的空间直角坐标系,设AD=a,则坐标分别为
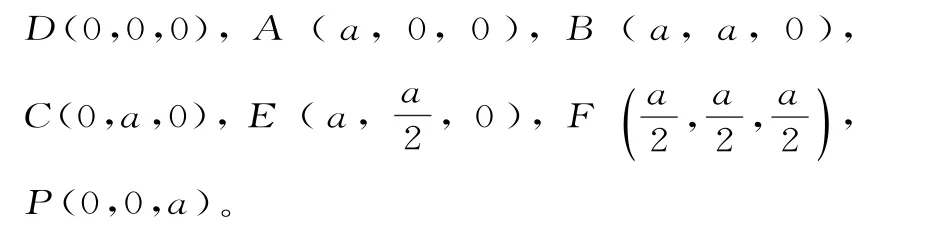
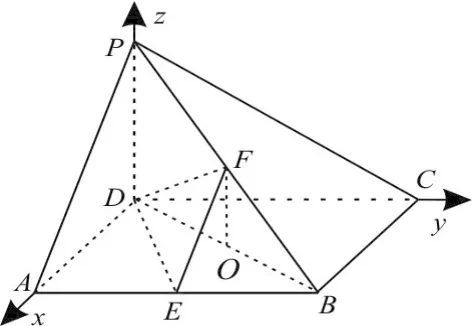
图4
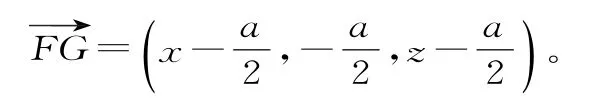
练一练:
1.在长方体ABCD-A1B1C1D1中,E、F分别是AD、DD1的中点,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图5所示的几何体ABCDA1C1D1,且这个几何体的体积为
(1)求证:EF∥平面A1BC1。
(2)求A1A的长。
(3)在线段BC1上是否存在点P,使直线A1P与C1D垂直?如果存在,求线段A1P的长;如果不存在,请说明理由。

图5
答案:(1)略;(2)4;(3)存在,
2.如图6,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=AB,M、N分别是PA、BC的中点。
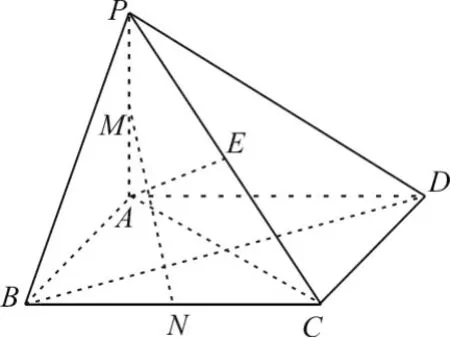
图6
(1)求证:MN∥平面PCD。
(2)在棱PC上是否存在点E,使得AE⊥平面PBD?若存在,求出AE与平面PBC所成角的正弦值;若不存在,请说明理由。
答案:(1)略;(2)点E存在,是PC的中点,正弦值为
3.已知M为正方体ABCD-A1B1C1D1的棱BC的中点,点P在面CC1D1D内,且PM∥平面BB1D1D,探讨点P的确切位置。
答案:点P在线段CD、C1D1的中点的连线上。
4.在棱长AB=AD=2,AA1=3的长方体ABCD-A1B1C1D1中,点E是平面BCC1B1上一个动点,点F是CD的中点,试确定点E的位置,使得D1E⊥平面AB1F。
答案:以A为原点,直线AB、AD,AA1为x轴,y轴,z轴建立空间直角坐标系,
(责任编辑 徐利杰)

