瞄准高考方向 学好空间向量
■湖北省武汉市黄陂区第六中学 梅 磊
瞄准高考方向 学好空间向量
■湖北省武汉市黄陂区第六中学 梅 磊
空间向量是解决立体几何问题的有力工具,下面以近三年高考数学全国Ⅰ卷中的立体几何解答题为例,带你瞄准高考方向,学好空间向量。
(2014年全国Ⅰ卷理第19题)如图1,三棱 柱 ABCA1B1C1中,侧面BB1C1C为菱形, AB⊥B1C。

图1
(1)证明:AC=AB1;
(2)若AC⊥AB1,∠CBB1=60°,AB= BC,求二面角A-A1B1-C1的余弦值。
解析:(1)连接BC1,交B1C于点O,连接AO。因为侧面BB1C1C为菱形,所以B1C⊥BC1,且O为B1C及BC1的中点。
又AB⊥B1C,所以B1C⊥平面ABO。由于AO⊂平面ABO,故B1C⊥AO。
又B1O=CO,故AC=AB1。
(2)因为AC⊥AB1,且O为B1C的中点,所以AO=CO。又因为AB=BC,所以△BOA≌△BOC。故OA⊥OB,从而OA, OB,OB1两两互相垂直。

图2
因为∠CBB1=60°,所以△CBB1为等边三角形。又AB=BC,则:
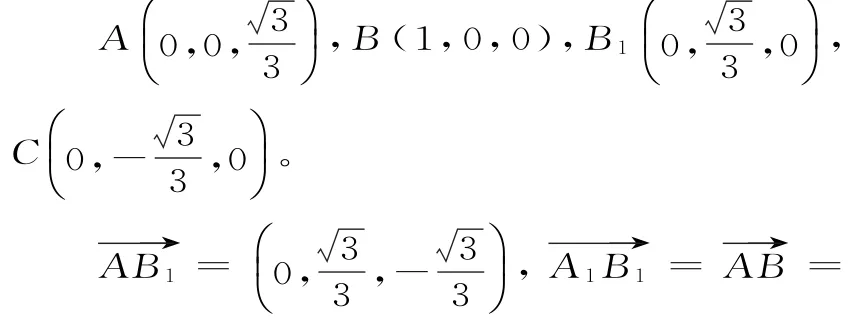
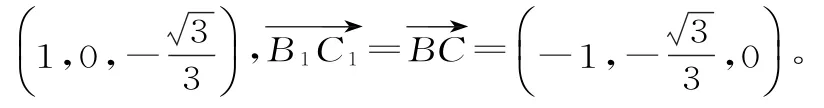
设n=(x,y,z)是平面AA1B1的法向量,则即
设m=(x,y,z)是平面A1B1C1的法向量,则
二面角A-A1B1-C1的余弦值为
点评:本题中以横放的三棱柱ABCA1B1C1为基本图形,侧面BB1C1C为菱形,有利于建立空间直角坐标系。
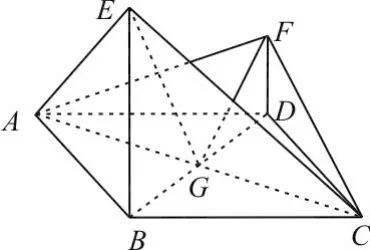
图3
(2015年全国Ⅰ卷理第18题)如图3,四边形ABCD为菱形,∠ABC=120°,E、F是平面ABCD同一侧的两点,BE⊥平面ABCD, DF⊥平面ABCD,BE=2DF,AE⊥EC。
(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值。
解析:(1)连接BD,设BD∩AC=G,连接EG,FG,EF。
在菱形ABCD中,不妨设GB=1。由∠ABC=120°,可得AG=GC=。
由BE⊥平面ABCD,AB=BC,可知AE=EC。
从而EG2+FG2=EF2,所以EG⊥FG。
又AC∩FG=G,可得EG⊥平面AFC。
又EG⊂平面AEC,则平面AEC⊥平面AFC。
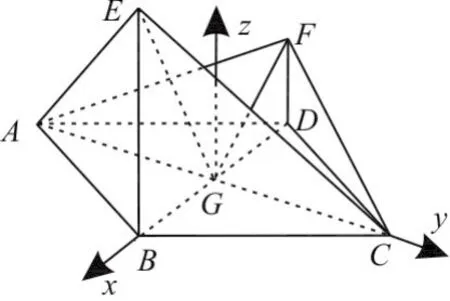
图4
故
点评:本题以同学们熟悉的菱形为载体,利用添加平面垂线段的方法构建空间几何图形,使大家感觉到“似曾相识”之中有新意。本题的立体图形情境是同学们在学习立体几何中的有关概念和线面关系的过程中所熟悉的,同学们可以根据题意,按部就班地解题。90°,且二面角D-AF-E与二面角C-BE-F都是60°。
(2016年全国Ⅰ卷理第18题)如图5,在以A、B、C、D、E、F为顶点的五面体中,面ABEF为正方形, AF=2FD,∠AFD=

图5
(1)证明:平面ABEF⊥平面EFDC;
(2)求二面角E-BC-A的余弦值。
解析:(1)由已知可得AF⊥DF,AF⊥FE,所以AF⊥平面EFDC。
又AF⊂平面ABEF,故平面ABEF⊥平面EFDC。
(2)过D作DG⊥EF,垂足为G,由(1)知DG⊥平面ABEF。
由(1)知∠DFE为二面角D-AF-E的平面角,故∠DFE= 60°,则|DF|=2,可得A (1,4,0),B(-3,4,
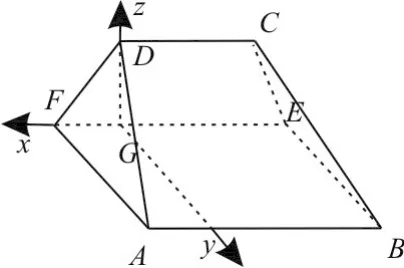
图6
因为AB∥EF,所以AB∥平面EFDC。
又平面ABCD∩平面EFDC=CD,故AB∥CD,CD∥EF。
由BE∥AF,可得BE⊥平面EFDC,所以∠CEF为二面角C-BE-F的平面角,∠CEF=60°。从而可得C(-2,0
设n=(x,y,z)是平面BCE的法向量,则满足:
点评:解立体几何问题,关键在于建立空间直角坐标系,把空间中的点用空间坐标表示出来。利用空间向量可解决平行、垂直关系的证明问题,其理论依据为向量的共线和数量积公式。
(责任编辑 徐利杰)

