例析圆锥曲线中的探索性问题
■重庆市铁路中学 何成宝
例析圆锥曲线中的探索性问题
■重庆市铁路中学 何成宝
圆锥曲线中的探索性问题,是同学们在学习圆锥曲线时经常遇到的一类问题,面对此类问题,同学们往往束手无策,难以顺利解决。下面举例说明,以供同学们参考。
一、椭圆
已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、 F、G分别在BC、CD、DA上移动,且=P为GE与OF的交点(如图1),问是否存在两个定点,使P到这两点的距离的和为定值。若存在,求出这两点的坐标及此定值;若不存在,请说明理由。
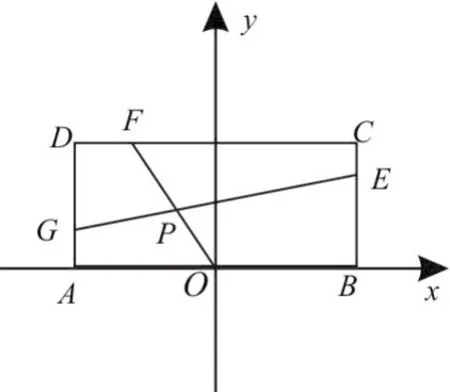
图1
解析:根据题设条件,首先求出点P的坐标满足的方程,据此再判断是否存在两定点,使得点P到两点距离的和为定值。
解得坐标分别为:A(-2,0),B(2,0), C(2,4a),D(-2,4a)。

解得坐标分别为E(2,4ak),F(2-4k, 4a),G(-2,4a-4ak)。
直线OF的方程为:

直线GE的方程为:

①②联立消去参数k,得点P(x,y)的坐标满足方程2a2x2+y2-2ay=0。
二、双曲线
解析:假设存在直线m,它与双曲线的交点Q1、Q2的坐标分别为Q1(x1,y1),Q2(x2, y2),则:
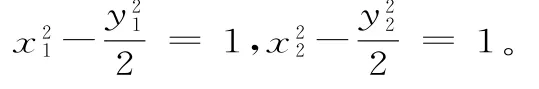
两式相减,得:

则2(x1-x2)=y1-y2。
直线m的方程为y-1=2(x-1),即y=2x-1。
2x2-4x+3=0。
Δ=(-4)2-4×2×3=-8<0。
因此,直线y=2x-1与双曲线不相交,题设中的直线是不存在的。
在研究直线与圆锥曲线有关的问题时,应注意对判别式的讨论。
三、抛物线
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,已知|AB|=2|OA|,且点B的纵坐标大于零。
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程。
(3)是否存在实数a,使抛物线y= ax2-1上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求出a的取值范围。
解析:(1)设,则由得
由条件可知圆的标准方程为(x-3)2+ (y+1)2=10,圆心为(3,-1),半径为。
设圆心(3,-1)关于直线OB的对称点为(x0,y0),则:得故所求圆的方程为(x-1)2+(y-3)2=10。
(3)设P(x1,y1),Q(x2,y2)为抛物线上关于直线OB对称两点,则:

x1,x2为方程的两个相异实根,于是由解得
以上三个例题,分别是椭圆、双曲线、抛物线与直线的关系中的探索性问题。探索性问题,由于没有明确的结论,方向不明,自由度大,要去探索研究。因此,学好圆锥曲线中的探索性问题,能够很好地培养同学们的创新意识和应用能力。
(责任编辑 徐利杰)
启事:随着高考制度的不断改革,全国参加高校自主招生的学生越来越多,为了更好地备战自主招生考试,本刊编辑部决定于今年5月份出版一期增刊,主要内容为全国部分高校自主招生面试、笔试典型题归类解析,定价6元,邮寄费1元。欢迎订阅。邮局汇款: (450004)郑州市顺河路11号《中学生数理化》(高中)编辑部。收款人:王福华。转账汇款:中国邮政储蓄,户名王福华,卡号6221884910016853274。
本刊编辑部

