例说数列与不等式的综合题型
■湖南省长沙市周南雨花中学 彭向阳
例说数列与不等式的综合题型
■湖南省长沙市周南雨花中学 彭向阳
一、不等式成立问题
已知等比数列{an}满足2a1+ a3=3a2,且a3+2是a2与a4的等差中项。
(1)求数列{an}的通项公式;
(2)若bn=an-log2an,Sn=b1+b2+…+ bn,求使不等式Sn-2n+1+47<0成立的n的最小值。
解析:(1)容易求得an=2n。
(2)bn=2n-log22n=2n-n。
故所求的n的最小值为10。
点评:正确利用求和公式求解,得到关于n的不等式,解不等式时,注意n是正整数。
二、不等式证明问题
设n∈N*,xn是曲线y=x2n+2+1在点(1,2)处的切线与x轴交点的横坐标。
(1)求数列{xn}的通项公式;
解析:(1)第一问简单,利用导数y'=(2n+ 2)x2n+1,求出切线方程y-2=(2n+2)· (x-1),再令y=0得到
(2)第二问难度大一点,有以下两种解法:
解法1:利用单调性。

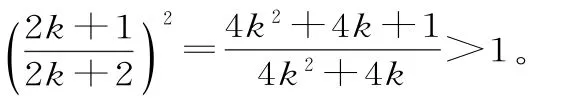
说明{n Tn}单调递增,于是nTn≥1·T1=,所以
解法2:利用放缩法。
放缩法一:
放缩法二:
放缩法三:
变式1 已知数列{an}中,a1=1,an+1=
(1)求数列{an}的通项公式;
(3)已知pn=(1+b1)(1+b3)(1+b5)… (1+b2n-1),求证:
解析:(1)由题意知,则整理得到

(3)原 不 等式 即为 pn=
故原不等式成立。
变式2 数列{an}的前n项和为Sn,且Sn=2an-1,设bn=2(log2an+1),n∈N*。
(1)求数列{an}的通项公式;
(2)求数列{an·bn} 的前n项和Tn;
(3)证明:对于任意n∈N*,不等式恒成立。
解析:(1)由题意知Sn=2an-1。①
当n≥2时,Sn-1=2an-1-1。②
由①-②得an=2an-1。
由于S1=2a1-1,所以a1=1,an=2n-1。
(2)bn=2(log2an+1)=2n。
故Tn=2·20+4·21+6·22+…2n· 2n-1。③
故2Tn=2·21+4·22+…+(2n-2)· 2n-1+2n·2n。④
③-④得:
-Tn=2+2(21+22+…2n-1)-2n·2n= (2-2n)·2n-2。
所以Tn=(2n-2)·2n+2=(n-1)· 2n+1+2。
(3)待证不等式两边平方得:


变式3 在数列{an}中,已知并且当n≥2且n∈N*时,有an+1=
(1)若bn=an+1-an(n∈N*),求证:数列{bn}是等比数列;
解析:(1)当n=1时
由累加法得到:

变式4 数列{an}的通项公式an=n+1。
解析:(1)设f(x)=sin,则结合函数y=cosx的单调性,知,函数f(x)在区间(0,x0)上递增,在上递减;又f(0)=,因此在上,恒有f(x)≥0,即sin
(2)因为anan+1≥6,所以由(1)知故


三、不等式恒成立问题
已知数列{an}是等差数列,a2= 6,a5=12,数列{bn}的前n项和是Sn,且
(1)求数列{an},{bn}的通项公式;
解析:(1)由题意容易求得an=2n+2,

点评:数列中的恒成立问题,同函数中的恒成立问题一样,m>an对任意的n∈N*都成立,则m大于an中的最大项;反之一样。这样转化为考虑数列的单调性,来求解最大值(上界)或者最小值(下界)。
变式1 已知数列{an}中,a1=2,anan-1-2n=0(n≥2,n∈N*)。
(1)求数列{an}的通项公式;
解析:(1)根据题意,利用累加法容易求得an=n(n+1)。
变式2 已知数列{an}中,a1=1,an+1=
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足数列{bn}的前n项和为Tn,如果不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围。
解析:(1)对原等式两边取倒数,得到令解得整理得
所以λ的取值范围是(-1,2)。
四、不等式有解问题
等差数列{an}的首项为a1,公差d=-1,前n项和为Sn,a1∈{1,2,3}。
(1)若存在n∈N*,使Sn=-5成立,求a1的值。
(2)是否存在a1,使Sn<an对任意大于1的正整数n均成立?若存在,求出a1的值;不存在,请说明理由。
解析: (1)由条件得Sn=na1+
整理得n2-(2a1+1)n-10=0。
由于n∈N*,所以Δ=(2a1+1)2+40必为完全平方数。
由于a1∈{1,2,3},逐个检验得a1=1符合要求,此时n=5。
(2)由Sn<an得:

故不存在a1,使Sn<an对任意大于1的正整数n均成立。
点评:不等式有解问题,同函数不等式的有解问题一样,实质也是最值问题。存在n∈N*使得m>an有解,则m大于an的最小项;m<an有解,m小于an的最大值。这样转化考虑数列的单调性,来求解最大值(上界)或最小值(下界)。
(责任编辑 徐利杰)

