浅谈抛物线几何性质的几何证明

■郑州外国语学校 杨春波

数学篇

浅谈抛物线几何性质的几何证明

■郑州外国语学校 杨春波

抛物线的一些几何性质想必大家是熟悉的:如图1,抛物线y2=2px(p＞0)的焦点为F,准线为l。过点F作倾斜角为α(0＜α＜π)的直线与抛物线交于A、B两点,设A(x1,y1), B(x2,y2),M为AB的中点,由A、M、B向准线l作垂线,垂足分别为D、N、C,连接图中剩余各线段,则有:

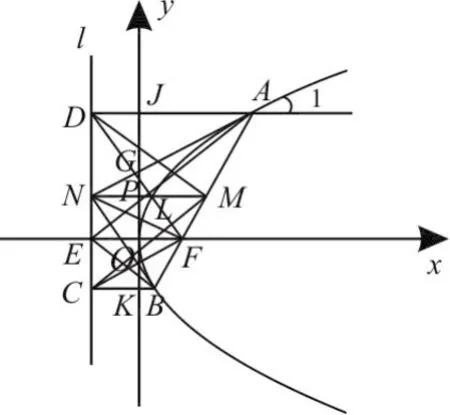
图1

(4)以AB为直径的圆与准线l相切。

(5)点A、O、C三点共线,点B、O、D三点共线。

证明抛物线的以上几何性质时多用代数方法(即联立直线与抛物线的方程),既然是几何性质,为何不用几何证法呢?而且,相对于椭圆和双曲线来说,抛物线的定义自有优势:平面内与一个定点和一条定直线(定直线不经过定点)距离相等的点的轨迹。现把抛物线几何性质的几何证明,展示如下。

证明:

因此,|AB|≥2p,当且仅当sin2α=1,即时,等号成立。这就是“通径在过焦点的所有弦中弦长最短,其长度为2p”。(3)得证。

由AD∥BC及AF=AD,BF=BC,易证∠DFC=90°。在Rt△DFC中,FE为斜边上的高,由射影定理知EF2=ED·EC,即y1y2=-p2。

Rt△DFC中,FN为斜边上的中线,则FN=NC=ND,从而易证△ADN≌△AFN (或△BCN≌△BFN),得∠NFM=90°,即NF为Rt△ANB斜边上的高,则NF2= AF·BF,从而:

易知|AB|=x1+x2+p。

由|AF|=|AD|=|EF|+|AF|cosα= p+|AF|cosα,得

设G为AN与DF的交点,H为BN与CF的交点,则G、H分别为DF和CF的中点。在△DEF中,G为DF的中点,O为EF的中点,故OG为△DEF的中位线,OG∥DE,点G在y轴上。同理,点H也在y轴上。而且易知G、H分别是OJ和OK的中点。

两式相乘,得AJ·BK·(OF)2= (OG·OH)2=(OF)4,AJ·BK=(OF)2,即至此(1)得证。

设AC与x轴的交点为O',则:

因此,|O'E|=|O'F|,O'为EF的中点,则O'与O重合,A、O、C三点共线。同理, B、O、D三点也共线,(5)得证。

值得一提的是,对于图1,有同学挖掘出了另外一些相关的几何性质和几何证明,补充在这里与大家分享。

(6)设L为MN与抛物线的交点,则L为MN的中点。

证明:在Rt△NFM中,由抛物线的定义知|LF|=|LN|,从而易证FL为斜边上的中线,则|LM|=|LN|,L为MN的中点。

(7)EF平分∠AEB。

证明:由知 Rt△ADE∽Rt△BCE,则∠AED=∠BEC,∠AEF=∠BEF,EF是∠AEB的平分线。(8)以AF或BF为直径的圆与y轴相切。

证明:设M1为AF的中点,则:

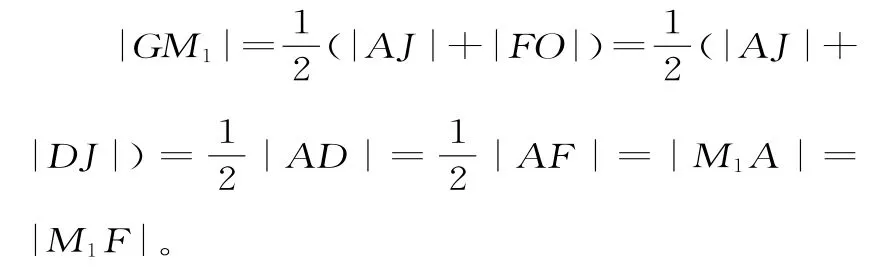
故以AF为直径的圆与y轴相切。同理,可证以BF为直径的圆也与y轴相切。

(9)NA、NB均是抛物线的切线。

证明:如图1,由∠FAN=∠DAN=∠1,结合抛物线的光学性质(从焦点出发的光线,经过抛物线上的一点反射后,反射光线平行于抛物线的轴),知NA是抛物线的切线。同理,NB也是抛物线的切线。

由此可见,抛物线的焦点弦在两端点处的切线互相垂直,且两切线的交点恰在抛物线的准线上,而且由NF⊥AB可知,两切线的交点与抛物线焦点的连线与焦点弦垂直。

众所周知,解析几何的基本思想是用代数方法研究几何问题,其最基本的研究方法为坐标法。但是,事物是一分为二的,如果过分强调坐标法,久而久之,人们就会习惯于将解析几何与繁难的运算等价起来,这样的认识是片面的。我们应该清楚地认识到,解析几何的研究对象是几何图形,因此,在解答解析几何问题时,要注重挖掘问题的几何特征,不妨用几何的眼光审视解析几何问题。更多的例证留给同学们去探索、去发现。

练一练:

1.已知抛物线y2=2px(p＞0)的焦点弦AB的两个端点分别为A(x1,y1),B(x2, y2),则的值一定等于( )。

A.-4 B.4 C.p2D.-p2

2.(2014·课标全国Ⅱ)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A、B两点,则|AB|等于( )。

3.过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,则|AF|·|BF|的最小值为( )

4.设抛物线x2=12y的焦点为F,经过点P(2,1)的直线l与抛物线交于A、B两点,且P恰为AB的中点,则|AF|+|BF|=____。

参考答案:1.A2.C3.C4.8

(责任编辑 徐利杰)