圆锥曲线的定义在解题中的运用

☉江苏省常熟市尚湖高级中学 王梅芳

圆锥曲线的定义在解题中的运用

☉江苏省常熟市尚湖高级中学 王梅芳

定义是揭示事物本质属性的思想形式，面对一个数学对象，回顾它的定义，常常是解决问题的锐利武器．圆锥曲线的第二定义体现了“形”的统一，第一定义则体现了“质”的区别．两种定义不仅在解题中应用广泛，而且具有很大的灵活性．第一种定义和第二种定义的灵活转换常常是打开解析几何思路的钥匙，在题目中挖掘这些隐含信息有助于解题．下面我们一起来看看圆锥“定义”在求解圆锥曲线问题中有哪些常规应用．

一、利用圆锥曲线定义解含绝对值不等式

我们知道，椭圆类不等式：|x-c|+|x+c|≤2a（a＞c）的解为-a≤x≤a；|x-c|+|x+c|≥2a（a＞c）的解为x≤-a或x≥a.类似的，双曲线类不等式：||x-c|-|x+c||≥2a（a＜c）的解为x≤-a或x≥a；||x-c|-|x+c||≤2a（a＜c）的解为-a≤x≤a.利用圆锥曲线定义可以解决这类绝对值不等式问题.

（一）椭圆类不等式

1.形如|MF1|+|MF2|≤2a（|F1F2|＜2a）

它表示椭圆类不等式，它的解集为｛x|xA≤x≤xB｝.

2.形如|MF1|+|MF2|≥2a（|F1F2|＜2a）

它表示椭圆类不等式，它的解集为｛x|x≤xA或x≥xB｝.

例1不等式|x-1|+|x+2|≥5的解集为________．

此题为椭圆类不等式．问题关键：用椭圆的定义求出它的中心、顶点即可．

解：根据椭圆类不等式2a=5，2c=1-（-2）=3，“中心”

所以不等式|x-1|+|x+2|≥5的解集为｛x|x≤-3或x≥2｝．

3.特别地，当|F1F2|=m，|MF1|+|MF2|=m（常数）

它不再表示椭圆，而动点M是线段F1F2上的任一点，而不等式|MF1|+|MF2|＜m表示三边不能构成三角形，所以不等式的解集为Ø；

|MF1|+|MF2|≥m表示三边可构成三角形或线段上任意一点，用三角形两边之和大于第三边推导，所以不等式的解集为R．

（二）双曲线类不等式

1.形如||MF1|-|MF2||≤2a（|F1F2|＞2a）

它表示双曲线类不等式，它的解集为｛x|xA≤x≤xB｝.

2.形如||MF1|-|MF2||≥2a（|F1F2|＞2a）

它表示双曲线类不等式，它的解集为｛x|x≤xA或x≥xB｝.

例2已知函数f（x）=|x-m|，其中m＞1.

（1）略.

（2）已知关于x的不等式|f（2x+m）-2f（x）|≤2的解集为｛x|1≤x≤2｝，求m的值．

这是一道关于绝对值的函数题，变形后变为含参数的绝对值不等式，观察到此题是双曲线类不等式，不妨找“中心”、找“顶点”，与已知解集采用数形结合可将问题解决.

解：（1）略.

（2）因为f（x）=|x-m|，其中m＞1，

所以将不等式|f（2x+m）-2f（x）|≤2转化为||x|-|xm||≤1.

根据双曲线类不等式2a=1，2c=m-0，“中心”为x=

xA，所以原不等式的解集为

由题的条件可知，不等式的解集为｛x|1≤x≤2｝，

3.形如|MF1|-|MF2|≤2a或|MF1|-|MF2|≥2a（|F1F2|＞2a）

它们表示双曲线类不等式的右支，它们的解集分别为｛x|x≤xB｝或｛x|x≥xB｝．

例3不等式|x+2|-|x|≤1的解集为________．

此类绝对值不等式是双曲线类不等式．因式子|x+2|长度较长，-2＜0，因此可判断双曲线类不等式的右支．解题的关键是求“中心”和“顶点”．

解：因“左焦点”-2在前，|x+2|长度比较长，因此本题属于双曲线类不等式的右支．

根据双曲线类不等式2a=1，2c=0-（-2）=2，“中心”为

由圆锥曲线定义知，xF1=-2，xF2=0，xA=-1

4．形如|MF2|-|MF1|≤2a或|MF2|-|MF1|≥2a（|F1F2|＞2a）

它们表示双曲线类不等式的左支，它们的解集分别为｛x|x≥xA｝或｛x|x≤xA｝．

5．特别地，当|F1F2|=m，||MF1|-|MF2||=m（常数）

它不再表示双曲线，而动点M表示以F1，F2为顶点的射线，简称为“两边开”．在涉及到不等式||MF1|-|MF2||≤m表示三边可构成三角形或线段上任意一点，用三角形两边之差小于第三边推导，所以不等式的解集为R；不等式||MF1|-|MF2||＞m表示三边不能构成三角形，所以不等式的解集为Ø．

（三）抛物线类不等式

形如|MF|≤d或|MF|≥d表示抛物线类不等式．由于抛物线只有一个顶点，所以不等式的解集显得简单些，结果要么左边开要么右边开．

二、求焦点三角形的面积

分析：首先设|PF1|=m，|PF2|=n，用余弦定理求得m与n之间的关系，再根据椭圆定义用配方法求得mn的值，代入三角形面积公式问题即可解决．

解：由题意得a=4，c=3，所以|F1F2|=2c=6．

设|PF1|=m，|PF2|=n，由余弦定理得

|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|·cos∠F1PF2，

即6=m2-n2-mn，所以36=（m+n）2-3mn．

由椭圆定义得m+n=2a=8，所以36=64-3mn，所以mn=

三、利用圆锥曲线定义求离心率

例5F1，F2是椭圆的两个焦点，过F2作一条直线交椭圆于P，Q两点，使PF1⊥PQ，且|PF1|=|PQ|，求椭圆的离心率e．

我们在解有关圆锥曲线问题时，如果题目涉及焦点、准线方程、离心率、圆锥曲线上的点这四个条件中的三个，我们一般就要联想到圆锥曲线定义，有时甚至只知道其中的两个条件，也可以联想到圆锥曲线定义．灵活巧妙地运用圆锥曲线的定义，将会带给我们意想不到的方便和简单．

四、利用圆锥曲线的定义求最值

例6如图1，F1，F2是双曲线的左、右焦点，M（6，6）为双曲线内部的一点，P为双曲线右支上的一点，求：

（1）|PM|+|PF2|的最小值；

图1

（其中|PH|为P到右准线l的距离）

说明：（1）和式“|PM|+|PF2|”与双曲线第一定义有质的区别，能否转化为“差”是解题的关键；（2）关键在于处理|PF2|的系数，于是联想到，可用第二定义转化．

五、求线段（或线段和）的长度

A.bB.aC.ebD.ea

分析：首先根据三角形内心的性质及等腰三角形的“三线合一”性质将|PF2|转化为|PC|，再根据三角形中位线定理和双曲线定义，问题即可解决.

解：延长F2B交PF1于C，则可知PB既为△PF2C角平分线又为△PF2C高线，所以△PF2C为等腰三角形，所以|PF2|= |PC|且|BF2|=|BC|，所以OP为△CF1F2的中位线，则|OB|=由双曲线定义知，|PF1|-|PF2|=2a，所以，故选B.

六、利用圆锥曲线的定义求动点轨迹方程

求动点轨迹方程，若动点运动规律或几何约束等式符合某一圆锥曲线的定义时，可直接确定其标准方程，并得出待定系数之值，从而直接得出结果．

例8过原点的椭圆的一个焦点为F1（1，0），长轴长为4，求椭圆中心的轨迹．

解：设椭圆中心为M（x，y），由于椭圆的一个焦点为F1（1，0），则椭圆的另一个焦点为F2（2x-1，2y），再由椭圆的定义知，|OF1|+|OF2|=4，即即（除去点（-1，0））.

此题看似简单，却是一道颇费思量的题目，当题中条件不易直接得出结论时，回归定义却是最好的办法．

七、求直线的斜率（或倾斜角）

例9已知直线l：y=k（x-2）（k＞0）与抛物线C：y2=8x交于A，B两点，F为抛物线C的焦点.若|AF|=2|BF|，求k的值.

分析：首先根据抛物线的定义将|AF|，|BF|转化为点A，B到准线的距离，再利用相似三角形和同角三角函数的基本关系式求得直线的斜率.

解：因为直线l过定点（2，0），那抛物线的焦点F，所以直线经过抛物线的焦点.分别过点B，A作抛物线准线的垂线，垂足分别为B′，A′，过B作AA′的垂线，垂足为D.设Rt△ABD，|BF|=m，因为|AF|=2|BF|，所以|AF|=2m.由抛物线定义得|BB′|=m，|AA′|=2m.在Rt△ABD中，|AD|=m，|AB|=3m.设直线l的倾斜角为θ，则θ=∠BAD.因为cosθ=也即直线的斜率为

图2

八、利用圆锥曲线定义巧解实际问题

图3

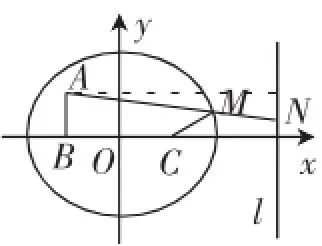
图4

实际应用问题要将问题转化为数学模型来解决.

解：由题意知，|MA|+|MB|=8＞4=|BC|，故点M在以B，C为焦点的椭圆上.如图4，建立平面直角坐标系xOy，则B（-2，0），C（2，0），所以点M的轨迹方程为.过M作MN⊥l于 N，则由椭圆的第二定义可知，|MN|=2|MC|.依题意知求|MA|+2|MC|的最小值，即求|MA|+|MN|的最小值.由平面几何知识可知，当M，A，N共线时，|MA|+|MN|最小.所以，即变电房应建在A村的正东方向且距A村

本解法综合考查了椭圆的第一定义以及标准方程，并利用椭圆的第二定义求最小值问题，特别是第二定义的应用，并借助了数形结合使问题得以解决.

从上面我们可以看出：运用圆锥曲线的定义解题，通过数形结合，不仅能抓住问题的本质，还能避开复杂的运算，使问题巧妙获解．要想利用定义解决问题，我们一定还要充分利用初中所学的平面几何的有关知识来辅助证明和解答.应用比较多的，如等腰三角形的“三线合一”性质、三角形中位线定理、线段垂直平分线的性质定理、角平分线的性质定理、勾股定理、相似三角形、特殊四边形的性质等知识.高中阶段主要和平面向量中向量共线的充要条件、圆的定义等知识结合使用.我们还会应用数形结合思想和转化思想来有效地处理题目中所涉及的多种元素之间的位置关系和数量关系.