一道模考题的题源探究

☉江苏省无锡市第一女子中学 王剑

一道模考题的题源探究

☉江苏省无锡市第一女子中学 王剑

考题（2016苏锡常镇一模·19）设函数f（x）=x-2exk（x-2lnx）（k为实常数，e=2．71828…是自然对数的底数）．

（1）当k=1时，求函数f（x）的最小值；

（2）若函数f（x）在区间（0，4）内存在三个极值点，求k的取值范围．

一、考题之解

分析：第（1）问通过求导，考查了导数的运算，难点是判断ex-x2=0是否有零点，因此我们不难发现当k=1时，这个函数的定义域为｛x|x＞0｝，于是第一种方法可将等式变形为x=2lnx，从而构造函数φ（x）=x-2lnx，通过导数的方式判断这一函数最小值是否大于0，另一种方法是构造函数h（x）=ex-x2，然后求导两次，可以得到当x=ln2时，h′（x）的极小值为2-2ln2，而这一数值是大于0的，于是可以得到h′（x）＞0即h（x）在（0，+∞）上单调递增，上述两种思路都是解决这一小问的可行之法．

第（2）问的难点是将极值点问题转化为零点问题，主要涉及函数与方程、数形结合这两大数学思想，本题考查的另一特色是重视列表检验，考查学生对导数的理解与运用．

下面给出证时：当x＞0时，ex＞x2．

证法1：当x＞0时，ex＞x2可变形为x＞2lnx．

令φ′（x）=0，x=2．

于是当0＜x＜2时，φ′（x）＜0；当x＞2时，φ′（x）＞0，故φ（x）=x-2lnx在x=2处取得最小值φ（2）=2-2ln2＞0，因此当x＞0时，x＞2lnx，所以ex＞x2．

于是当0＜x＜2时，f′（x）＜0，当x＞2时，f′（x）＞0．

所以f（x）在（0，2）上为减函数，在（2，+∞）上为增函数，所以f（x）在x=2处取得最小值

证法2：设h（x）=ex-x2，h′（x）=ex-2x，h″（x）=ex-2．

令h″（x）=0，解得x=ln2．

当x变化时，h′（x）与h″（x）的变化情况如下表：

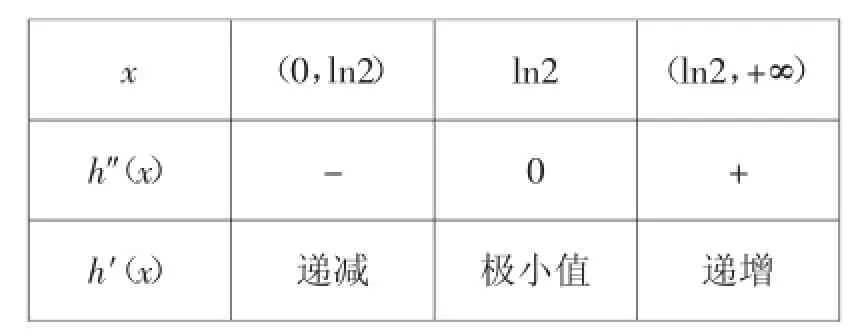
由表格可以看出：当h′（x）＞0，即h（x）=ex-x2单调递增，即h（x）＞h（0）=1.

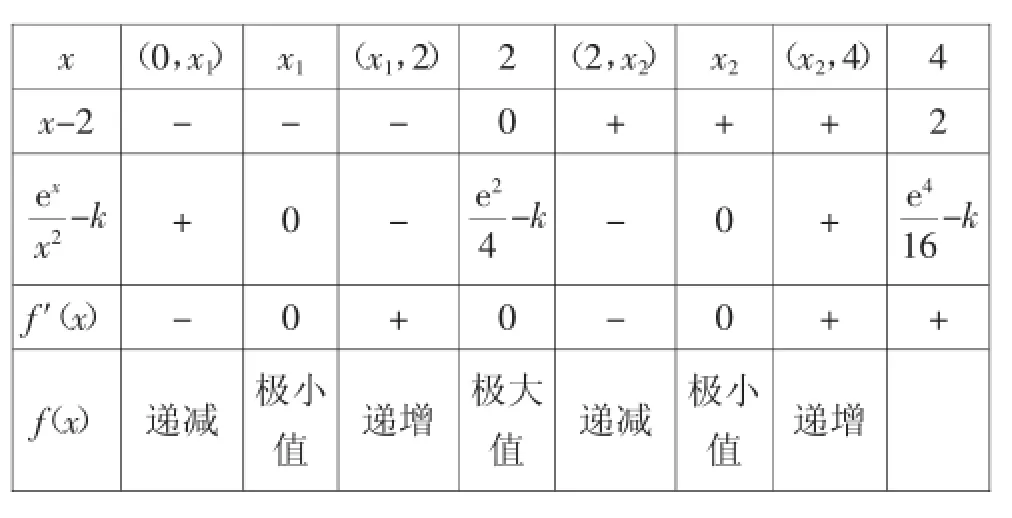
故f（x）在（0，x1）上单调递减，在（x1，2）上单调递增，在（2，x2）上单调递减，在（x2，4）上单调递增，所以f（x）在区间（0，4）上存在三个极值点，即函数f（x）在（0，4）内存在三个极值点的k的取值范围是

点评：1．导数及相关内容一直是近几年高考的重点和难点之一，在江苏省2016年高考数学考试说明中对本内容的考查主要有：

（1）导数的几何意义，B级要求，理解导数的几何意义是曲线上在某点处的切线的斜率，能够解决有关切线的问题；

（2）导数的运算，B级要求，熟练掌握导数的四则运算以及复合函数的导数运算是解决导数问题的基础；

（3）利用导数研究函数的单调性与极值，B级要求，也是解决导数类问题的核心方法；

（4）导数在实际问题中的应用，B级要求，为探究函数类应用问题及简单的数学建模问题提供了比较好的研究手段．

2．利用导数方法证明不等式f（x）＞g（x）在区间D上恒成立的基本方法是构造函数h（x）=f（x）-g（x），然后根据函数的单调性或者函数的最值证明函数h（x）＞0，其中一个重要技巧就是找到函数h（x）在什么地方可以等于零，这往往就是解决问题的一个突破口．利用函数的导数研究不等式恒成立问题是一类重要题型，体现了导数的工具性作用，将函数、不等式紧密结合起来，考查了学生综合解决问题的能力．

二、考题之源

笔者发现这一模考题与其他省份的一些高考真题颇为相像，如2014年山东高考数学第20题：

（1）当k≤0时，求函数f（x）的单调区间；

（2）若函数f（x）在（0，2）内存在两个极值点，求k的取值范围．

参考答案：（1）函数f（x）的单调递减区间为（0，2），单调递增区间为（2，+∞）．

又如2013年陕西高考数学第21题：

已知函数f（x）=ex，x∈R．

（1）若直线y=kx+1与f（x）的反函数的图像相切，求实数k的值；

（2）设x＞0，讨论曲线y=f（x）与曲线y=mx2（m＞0）公共点的个数．

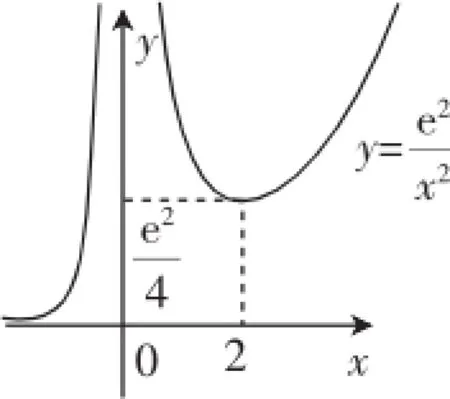
图1

我们不难发现，当x＜0时，函数单调递增，比较容易研究，所以上述的三道考题中均研究的是当x＞0时函数的性质．2016年江苏省苏锡常镇数学一模第19题第（2）问实质上是经过变形可以转化为当k取何值时函数与函数y=k在（0，4）内有两个交点，如若对图形分析到位，则不难发现结论．在2014年山东高考第20题第（2）问和2013年陕西高考第21题第（2）问均可“一望而解”．

三、题源之思

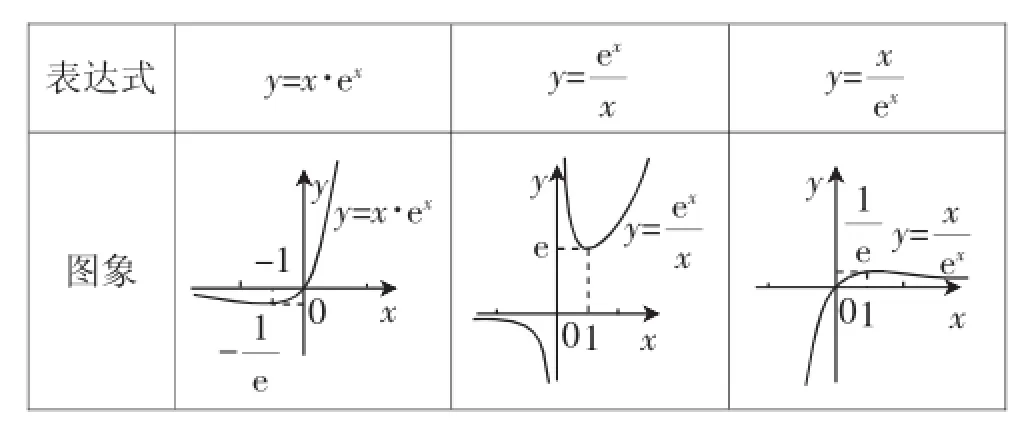
笔者认为这样的梳理不仅有利于学生对函数的分析和作图能力，更能够以这些函数模型作为题源衍生很多的函数好题，能够让学生从命题者的角度分析问题，让学生见到类似问题时不陌生，更快速地找到解题思路，有利于缓解考试遇难的焦虑情绪．

不妨来看一下2016年新课标数学全国Ⅱ卷理科第20题：

解：（1）f（x）的定义域为（-∞，-2）∪（-2，+∞），

所以f（x）在（-∞，-2），（-2，+∞）上单调递增．

当x＞0时，f（x）＞f（0）=-1，所以（x-2）ex＞-（x+2），即（x-2）ex+x+2＞0．

由（1）可得f（x）+a单调递增，对任意的a∈［0，1），f（0）+a=a-1＜0，f（2）+a=a≥0，所以存在唯一的x0∈（0，2］，使得f（x0）+a=0，即g′（x）=0．

当0＜x＜x0时，f（x）+a＜0，g′（x）＜0，g（x）单调递减；

当x＞x0时，f（x）+a＞0，g′（x）＞0，g（x）单调递增．

因此g（x）在x=x0处取得最小值，最小值为

因为x0∈（0，2］，所以h（0）＜h（a）≤h（2），即h（a）∈

综上，当a∈［0，1）时，函数g（x）有最小值．h（a），函数h（a）的值域为

点评：本题的考点是函数的单调性和极值等问题，尤其是第（2）题，先用导数法求函数g（x）的最值，再构造函数，又用导数法求解．这样的计算量对学生来说想要做全对不是很容易，如果在构造函数h（a）=时，能够通过已经掌握的知识得出这个函数的性质和大致图像，对求解是有很大的帮助的，华罗庚先生也提出“以形助数”的思想，实际上就是数形结合来看函数问题，类比表3，不难发现这一函数与极为相似，我们可以大胆猜测函数h（a）的一条渐近线为x=-2，从而作出草图如图2，则也不难发现当x0∈（0，2］时，h（a）这道高考题即是由基本的函数模型作为题源展开得来的，像这样的题目还有很多．

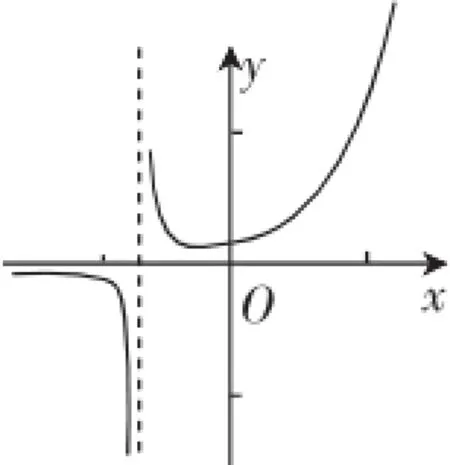
图2

高考命题每年都有变化，但经过仔细分析比较研究以后还是能够发现其中的规律，高考考题也不是凭空捏造，题目本身都有一定的母题和题源，掌握这些题源，无论高考考题千变万化，也能从容应对．