短生命周期乳制品供应链网络成本与收益优化研究
郭传好, 陈 芳, 单而芳
(1. 浙江理工大学经济管理学院, 浙江 杭州 310018;2.国药集团医药物流有限公司信息与供应链服务部, 上海 200443;3.上海大学管理学院, 上海 200444)
短生命周期乳制品供应链网络成本与收益优化研究
郭传好1, 陈 芳2, 单而芳3
(1. 浙江理工大学经济管理学院, 浙江 杭州 310018;2.国药集团医药物流有限公司信息与供应链服务部, 上海 200443;3.上海大学管理学院, 上海 200444)
供应链网络研究的目的之一就是在整个供应链满足顾客一定产品需求量的条件下,达到供应链的总成本最小以及总收益最大。本文针对短生命周期乳制品具有多品种,不易保存等特点及其在配送运输过程中的特殊要求,研究了其供应链网络的相关成本与收益问题。在满足顾客一定产品需求量的前提下, 建立了使得供应链的总成本与收益能够同时达到最优的双目标混合整数规划模型。其中, 为了有效刻画产品在零售商处的实际库存水平,本文引入了一个新的非线性函数来定义产品的实时库存量。基于模型的结构特点, 设计了一个新的增广ε-约束方法求解原模型。 实证分析结果表明,所建立的模型不仅能够为供应链提供整体成本与收益最优的决策方案,而且所设计的方法要优于标准的ε-约束方法。相关研究成果对研究优化供应链成本与收益, 以及提升顾客满意度等具有重要的潜在指导意义.
供应链网络;成本优化;收益优化;双目标混合整数规划;增广ε-约束方法
1 引言
随着人们生活水平的提高和膳食结构的改善,乳制品现已是人们日常生活中一种重要的营养食品,其在国内的消费市场正在不断的扩大, 尤其是对短生命周期乳制品(如酸奶,纯奶等)的消费需求呈现高速增长态势。 这不仅给物流企业带来了新的发展机遇, 同时也带来了挑战。因为短生命周期乳制品具有品种多, 易变质等特点, 且其在整个供应链中的生产,加工及配送运输等都需要在严格的温度与卫生等环境下进行,所以其供应链的成本相对于普通产品而言要高出许多。但供应链中各节点成员都希望在成本最小,收益最大的条件下去最大满足顾客的产品需求量。 因此,研究如何合理安排短生命周期乳制品的订购, 生产与配送方案,在满足顾客一定产品需求量的条件下使得其供应链的成本与收益最优,具有重要的理论意义和实际应用价值。
当前, 国内外许多学者从乳制品供应链的不同问题角度出发,对其进行了相关研究。 Qian Guixia等[1]以呼和浩特为研究案例,研究了乳制品供应链的收益分配问题,并提出了一个供应链各节点成员都满意且双赢的收益分配模型。 吴继贵和叶阿忠[2]对FMCG(快速消费品)供应链的风险进行分析,提出适用于FMCG供应链的风险评估指标, 并采用模糊综合评价分析法对中国乳制品供应链的风险情况进行综合分析。Bilgen和Celebi[3]研究了乳制品生产线上多种酸奶生产调度和配送的规划问题,并建立了一个线性混合整数规划模型,给出每个生产线的最佳生产计划和配送计划。Nicholson等[4]以美国乳制品为例,研究了多产品的食物供应链设施选址对供应链各部分成本的影响,提出了一个转运模型, 使得供应链的总成本最小。Sel等[5]针对酸奶生产的整体计划与调度问题,建立了混合整数线性规划模型, 并设计了启发式算法求解。Xu Jiuping等[6]以新禧乳品控股有限公司为例,在每个配送中心成本和运输成本固定的条件下,研究了供应链的配送中心选取问题以达到供应链的总成本与运输时间最小,并建立了带有随机模糊约束的多目标优化模型。
此外, Chen Xin等[7]以实现总期望收益最大化为目标, 在考虑订购成本,库存成本, 延期交货和损失订单的惩罚成本的基础上,研究了固定生命周期的易腐品的联合定价和库存控制问题。李贵萍等[8]以平均利润最大化为决策目标, 研究建立了非立即变质品的库存策模型。徐贤浩等[9]基于使用斜坡型函数描述短生命周期产品需求变化特征和用持有成本不断增加的形式来表示存货的无形变质所带来的损失等,建立了短生命周期产品的库存模型, 并给出了最优解的求解方法。基于供应链匹配理论, 陈芳等[10]研究了乳制品供应链网络的设计其相关成本优化问题。Ayag等[11]提出了一个模糊质量功能部署方法来判定乳制品行业中物流要求与供应链管理策略对顾客满意度的影响, 并将研究成果应用到土耳其的一个乳制品公司中。Manikas和Manos[12]建立了食品供应链的一个可追溯系统模型,其可作为乳制品行业中产品可追溯性管理系统web应用程序的开发基础。Miori和Segulin[13]针对牛奶等饮料单生产线产品生产调度问题给出了一个三联体符号模型,Lagrange松弛和动态规划方法用于求解问题的最优解。范体军等[14]针对生产商隐瞒新鲜度信息的生鲜农产品供应链协调问题,基于Stackelberg博弈, 使用单周期报童模型分别构建生产商和零售商的利润函数, 分析供应链性质并给出了具体的回购契约形式。 赵忠等[15]研究了由1个分销商与1个零售商和若干顾客构成的易腐品冷链系统,在变质率为常数, 需求为线性时变函数的情形下, 构建了两级信用支付条件下的零售商库存模型, 证明了最优解的存在性和唯一性。
综上可见, 当前关于短生命周期乳制品供应链相关成本与收益优化问题研究的成果比较少, 大多是针对乳制品供应链的风险评估,设施选址, 生产计划与调度和产品的定价与库存控制等问题, 以及一些具体的乳制品或乳制品公司的相关问题进行研究的, 没有充分考虑到短生命周期乳制品自身的特点及其对供应链网络的特殊要求, 以及没有将供应链网络的整体成本与收益等问题统一结合起来研究。
基于上述研究中存在的问题, 本文将针对短生命周期乳制品供应链网络的成本与收益问题进行整体的分析研究,建立相关问题的统一数学模型并给出求解方法。 首先,具体分析短生命周期乳制品的生产与运输的特殊性及其对配送网络的特殊要求。 其次,在满足供应链网络中零售商处顾客对相关产品一定数量需求的前提下,建立了能够使得整个供应链网络的成本与收益同时达到最优的数学模型,即为一个双目标混合整数规划模型。 同时,为了有效刻画零售商处相关产品的库存量随时间而不断变化的关系,引入了一个新的非线性函数来定义产品的实时库存量。 根据模型的结构特点,设计了一个新的增广ε-约束方法求解原问题。 最后,实证分析结果表明所建立的模型不仅能够为供应链提供整体成本与收益最优的产品生产与运输计划决策方案,而且所设计的方法要优于标准的ε-约束方法。相关研究成果对于进一步研究优化供应链的成本与收益, 以及提升顾客满意度等具有重要的潜在指导意义。
2 供应链网络成本及收益优化模型
短生命周期乳制品供应链主要由奶牛养殖户(场), 奶站,乳制品加工生产企业, 配送服务中心, 产品销售商及最终消费者等构成,如下图1所示,其网络设计的主要目标是用最短的时间, 最高的质量,最低的成本和优质的服务赢得顾客和市场。 由于短生命周期乳制品有小批量,多品种, 易变质和按订单生产提前期短等特点,其实际需求量还与产品的口味, 包装设计, 季节变化, 消费群体的年龄结构等实际因素有关。 产品原材料羊奶等动物鲜奶,其保存条件温度要求严格且易变质, 一般都要求其加工厂距奶源较近。 同时,为了保护奶源生产环境和消费者生活环境,以及防止工厂生产活动对居民生活环境造成影响,又要求乳制品的加工厂距消费者市场较远。 此外,其产品在运输过程中对运输条件及设备都要求较高, 例如需使用冷冻柜,冷藏车, 卫星定位系统等。 又由于产品加工厂远离消费者市场,零售商比较分散等原因, 在产品从生产商运输至零售商过程中,建立或租赁适当的配送中心十分必要,否则会导致产品在运输过程中的变质及产品不能及时配送到零售商处等损失。
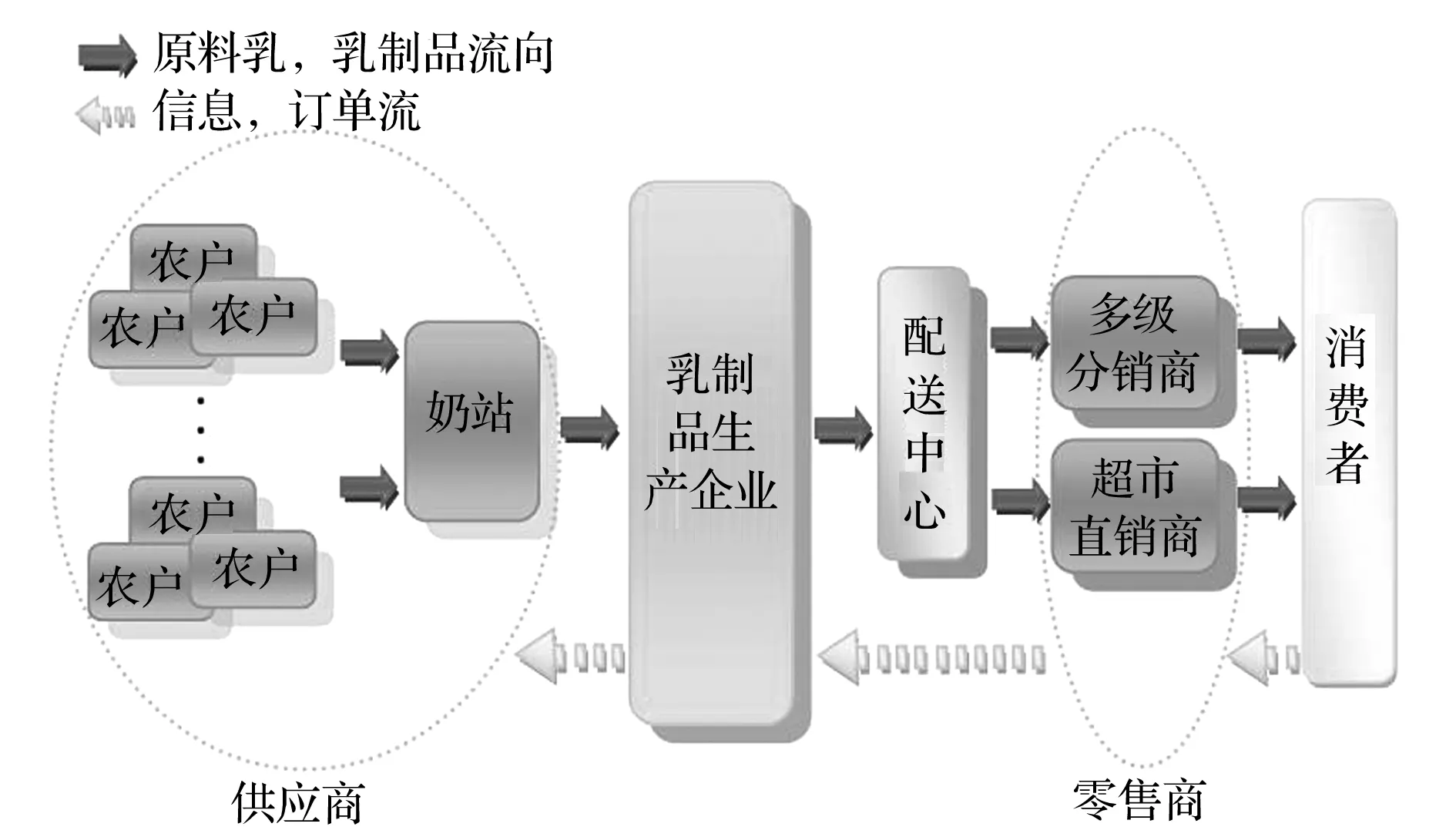
图1 短生命周期乳制品供应链网络结构图
基于上述分析,本文将研究图1所示的供应链网络在满足顾客一定产品需求量的条件下,如何分配产品在供应链各个节点的配送计划,使得供应链的整体成本最小和收益最大。 为了简化对奶源提供商的分析,本文将奶牛养殖户与奶站等整体视为供应商,同时鉴于短生命周期乳制品在实际中的生产, 配送运输和销售是一个动态的,多周期的过程, 本文仅考虑相关产品在一个周期中的生产,配送运输和销售情况。
优化模型的建立基于零售商在满足顾客一定产品需求量的前提下,产品一次采购而引起的供应链成本和收益问题,其中成本包括原材料的生产成本, 产品的生产成本, 配送中心的运营成本,零售商的采购成本以及整个供应链的运输成本等, 收益则分别考虑供应商,生产商和零售商的收益。 为了有效建立相关问题模型,本文假设原材料和产品在整个运输过程中无变质或损坏,供应商生产的原材料和生产商生产的产品瞬时交货, 即无相关库存费用,产品在运输至配送中心时及时配送, 亦无库存费用。
2.1 参数与决策变量
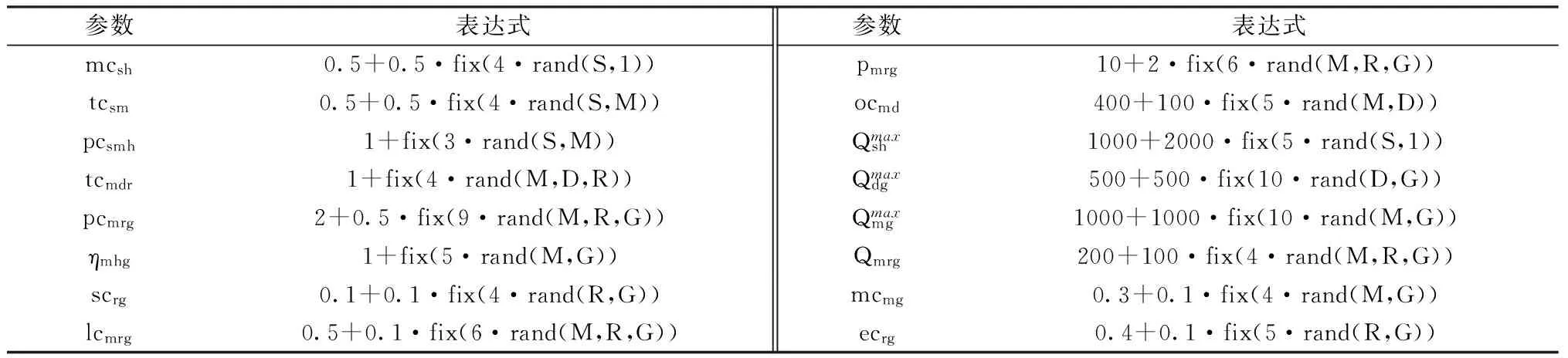
根据图1所示供应链网络的结构特点和建模的需要,模型中所涉及的参数及其含义首先定义如表1中所示, 其中,s,m,d和r分别表示供应链中的供应商, 生产商, 配送中心和零售商。
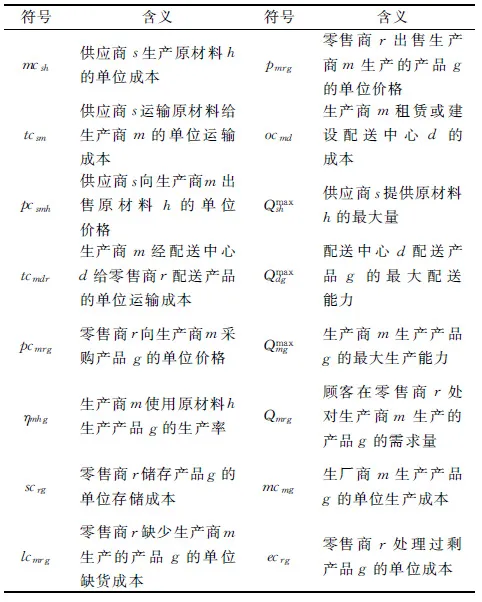
表1 参数符号及其含义
为了分析产品在供应链中各个节点成员处的配送计划, 以及度量供应链的成本和利润, 图1供应链中的决策变量定义如下:Nsmhg表示生产商m向供应商s采购用于生产产品g的原材料h的数量,Nmdrg表示生产商m经配送中心d配送给零售商r的产品g的数量,Nmrg表示零售商r向生产商m采购产品g的数量。 此外,Zsm表示生产商m是否选择供应商s采购原材料,Xmd表示生产商m是否选择配送中心d配送,Ymr表示零售商r是否选择生产商m采购产品, 这三个是0-1整数变量。
2.2 成本分析
基于上面定义的参数及决策变量, 分析图1中的供应链网络结构易知其成本由供应商成本, 生产商成本以及零售商成本组成。下面将分别说明各成本的相应组成部分, 并建立相关数学表达式。
首先是供应商成本SC。 根据假设条件和供应商在整个供应链中的作用,可知其成本主要包括生产原材料的成本及运输原材料给生产商的运输成本。根据表1中相关参数定义即得

其次, 生产商在供应链中的成本MC主要是由其采购原材料, 生产产品,产品配送运输以及配送中心运营等部分成本构成,根据参数的定义可得其表达式如下
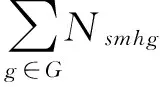
下面是零售商成本RC。 通过分析可知其由产品采购与库存成本, 产品在到达其销售限制时间时, 由于采购量与消费者实际需求之间的误差而导致产品不足或过剩而产生的产品缺货或过剩的处理成本组成。 鉴于短生命周期乳制品的特殊性, 其产品在到达零售商处开始销售时, 由于其比较新鲜, 同时顾客的需求也会比较集中, 因而会销售的较快。 随着顾客需求量被逐渐的满足, 产品的销售速度会逐渐变慢近似趋于平稳。 所以产品在到达其相应销售时间限制时, 其必会出现如下情形之一:I.产品过剩(供大于求),II.产品销售完全(供求平衡),III.产品缺货(供小于求)。
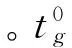
(1)
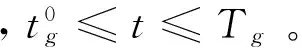

图2 产品库存水平曲线图
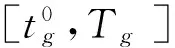
(2)
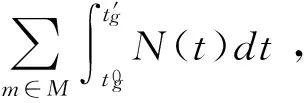
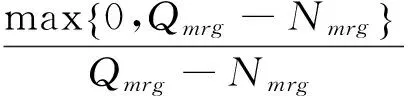
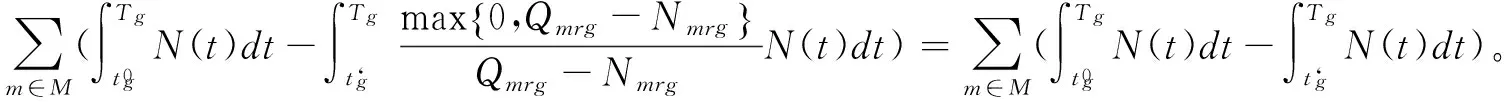
(3)
其中, 如果x>0,sign(x)=1, 如果x=0,sign(x)=0, 如果x<0,sign(x)=-1。 这样上式左端表达式则转化为是关于Nmrg的一个线性函数。
结合表达式(1), (2)和(3), 可得零售商的库存成本为:
(4)
此外, 当Nmrg与Qmrg不相等时, 则会出现产品过剩或缺货, 均会产生处理成本, 其相关成本表达式如下:
(5)
最后, 是零售商的采购成本:
(6)
综合上面关于零售商各部分成本的表达式可得其总成本表达式如下:
RC:=(4)+(5)+(6)
至此, 综上可得图1所示的供应链网络的总成本目标函数为:
SUMC=SC+MC+RC
2.3 收益分析
根据图1所示的供应链网络结构, 其收益主要由三部分组成, 分别为供应商销售原材料的收益, 生产商与零售商销售产品的收益,下面将分别建立相关收益的数学表达式。
首先是供应商的收益SR, 结合表1中参数的定义, 可得其表达式如下:
其次, 生产商的收益MR为:
最后是零售商的收益RR。 一般情况下, 产品的售价会随着销售时间的增加, 尤其是接近产品保质期时, 零售商通常会通过降低产品的价格来促进产品的销售, 且售价在某个时间段内是不变的。 基于短生命周期乳制品的特点, 其生命周期短且销售速度较快, 本文假定其销售价格在销售周期内是一定值。 因此, 可得零售商的收益为:
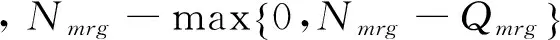
根据上面关于图1所示供应量网络中各个组成部分收益的分析, 立得待求解的总收益目标函数为:
SUMR:=SR+MR+RR
2.4 约束条件及优化模型
由于供应链网络在实际运行中, 其各节点成员会受到生产能力, 配送能力,存储能力或产品需求度等各方面条件的限制,下面将分别建立图1供应链网络中各节点成员间的约束关系。
首先, 关于供应商的约束条件主要是其生产和销售原材料的关系, 即:
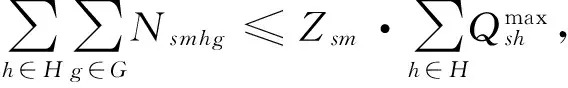
(7)
其表示供应商s销售原材料给生产商m的数量不能超过其能够提供的最大数量。
对于生产商, 其相关约束条件主要是产品生产能力的限制以及要满足零售商的产品需求量:
(8)
其中, 第一个式子表示生产商m所生产的产品g数量不能超过其采购的原材料能够生产出相应产品的数量, 同时也不能超过其生产该产品的最大生产能力。 第二个式子表示生产商生产的产品数量与零售商向其订购的相应产品数量相同。
此外, 在产品的配送运输过程中, 由于零售商距离生产商远近各不相同以及一些其他因素的影响。 有些零售商订购产品的配送需要经过配送中心的中转。 由配送中心重新整理分配产品, 再一次配送给相应的零售商。 同时, 每个配送中心的产品存储能力和相应的租赁费用也不相同, 因此, 配送中心在产品的实际配送过程中还受到下面的条件约束:
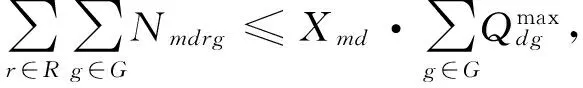
(9)
满足顾客需求不仅是供应链管理和优化的最终目标, 也是零售商拓宽市场, 增加收益的重要方法和途径之一。 因此, 零售商在向生产商下达产品订购计划前, 需系统总结产品在上一个周期的销售情况, 同时结合在下一周期内可能出现影响产品销售的因素, 来合理预测顾客在下一周期对产品的需求量, 进而制定相关产品的采购计划。 为了达到这一目的, 本文引入下面的约束条件:
(10)
来控制零售商的产品订购量, 其中,γ、β是零售商的预测误差, 0≤γ≤1,0≤β≤a0,a0是一个参数,其值根据产品实际销售情况而确定。
最后, 是关于整个供应链中决策变量的约束条件:
(11)
其中,Z+表示正整数集合。
至此, 图1所示供应链网络的约束条件已建立完成, 结合上面所建立的成本与收益目标函数, 即得本文要求解的模型如下:
minSUMC
(M1) maxSUMR
s.t. (7)-(11)。
很显然, 该问题是一个包含着两个目标函数, 且两个目标有着相互冲突利益的多目标混合整数规划问题, 其通常只有有效解, 而无最优解。 同时注意到目标函数SUMR是线性的, 而目标SUMC是非线性的, 主要是因为零售商成本RC中含有其产品库存成本的非线性计算表达式(4)。 为了有效求解该问题, 本文将基于模型(M1)的结构特点, 设计一个新的ε-约束方法, 并给出相关方法的流程图。
3 增广ε-约束求解方法
ε-约束方法[16]是求解多目标规划问题的最有效方法之一,其主要思想是通过引入参数, 将原问题转化为单目标规划问题,通过调整参数和求解单目标规划问题, 进而求得原问题的有效解。 很显然,模型(M1)是一个仅含有二个目标函数的多目标规划问题。 基于此,本节将设计一个新的ε-约束方法来求解模型(M1)。
首先, 标准的ε-约束方法求解模型(M1)的主要步骤如下: 通过引入参数Cε或Rε, 对模型(M1)进行转化, 可得:
maxSUMRminSUMC
(M1R-Cε)s.t.SUMC≤Cε,或(M1C-Rε)s.t.SUMR≥Rε
(7)-(11) (7)-(11)
其中,Cε,Rε分别为供应链总成本和收益的一个界的限制, 其通常根据经验或实际要求设置其数值。
然后, 调整参数Cε或Rε的大小, 并通过求解模型(M1R-Cε)或(M1C-Rε), 进而得到原问题模型(M1)的有效解。 其中, 下面的两个定理能够保证模型(M1R-Cε)或(M1C-Rε)与模型(M1)之间解的存在性及其等价关系。
定理1[17]如果是模型(M1)的有效解, 当且仅当存在Cε使得是模型(M1R-Cε)的最优解, 或当且仅当存在Rε使得是模型(M1C-Rε)的最优解。
定理2[17]如果是模型(M1R-Cε)或模型(M1C-Rε)的最优解且唯一, 那么是模型(M1)的有效解。
值得注意的是, 模型(M1R-Cε)或模型(M1C-Rε)中的目标函数仅为原模型(M1)目标函数中的一个, 与另外一个目标函数没有任何关联, 这样得到的最优解对于另外一个目标函数而言可能不是最优的, 尤其是当参数Cε或Rε的取值与供应链最优的成本或收益值误差较大时。 为了尽可能多的同时优化原模型中的目标函数, 同时给出参数Cε或Rε一种合理有效的取法, 本小节将设计给出一个新的增广ε-约束方法来求解模型(M1)。
首先, 为了给参数Cε或Rε的选取提供一个合理可靠的参考准则, 其相关最小或最大界值通过求解下面的模型得到
(M1R) maxSUMR
s.t. (7)-(11),或
(M1C) minSUMC
s.t. (7)-(11),
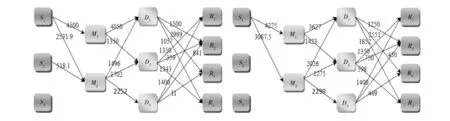
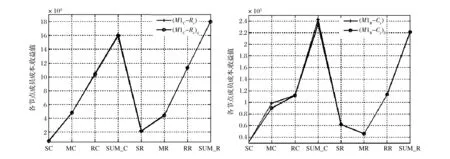
其中, 记模型(M1R)和(M1C)的最优值分别为Rmax和Cmin。 因此, 实际中参数Cε或Rε的选取就要求Cε>Cmin或Rε 其次, 为了利用ε-约束方法中处理目标函数的方法, 同时尽可能同时优化模型(M1)中的两个目标函数, 在模型(M1R-Cε)或(M1C-Rε)中, 分别引入参数0<δ,σ<1, 得到下面新的模型: maxSUMR+δ(Cε-SUMC) (M1R-Cε)δs.t.SUMC≤Cε (7)-(11) 或 minSUMC-σ(SUMR-Rε) (M1C-Rε)σs.t.SUMR≥Rε (7)-(11) 很显然, 模型(M1R-Cε)δ或(M1C-Rε)σ比模型(M1R-Cε)或(M1C-Rε)在目标函数中增加了一项δ(Cε-SUMC)或-σ(SUMR-Rε), 这使得在求解模型(M1R-Cε)δ或(M1C-Rε)σ时, 不仅优化了目标SUMR或SUMC, 同时通过调整参数Cε或Rε, 也能够有效的优化约束条件SUMC≤Cε或SUMR≥Rε, 尤其是当参数Cε或Rε的选取接近Cmin或Rmax时, 其分别也对另外一个目标函数进行了有效的优化。 因此, 模型(M1R-Cε)δ或(M1C-Rε)σ的求解结果要更优于模型(M1R-Cε)或(M1C-Rε)的结果, 其相关对比计算效果将在下一节中给出。 下面的定理则是进一步从理论上说明了新模型(M1R-Cε)δ或(M1C-Rε)σ的结果优于标准的模型(M1R-Cε)或(M1C-Rε)。 定理3模型(M1R-Cε)δ得到的利润值不小于模型(M1R-Cε)得到的利润值; 模型(M1C-Rε)σ得到的成本值不大于模型(M1C-Rε)的成本值。 证明: 定理两部分结论的证明过程类似, 在此只证明定理的第一部分的结论, 第二部分的结论可用相同的方法得到。 为了证明叙述的方便, 记模型的最优值为Opt(·), 模型(M1R-Cε)δ和(M1R-Cε)的最优解分别为X*和Y*。 很显然, 模型(M1R-Cε)δ和(M1R-Cε)的约束条件相同, 即它们的最优解也是彼此的可行解, 所以我们有: Opt(SUMR+δ(Cε-SUMC))X*≥Opt(SUMR +δ(Cε-SUMC))Y*≥Opt(SUMR)Y* Opt(SUMR)X*≥Opt(SUMR)Y* 其表明模型(M1R-Cε)δ得到的利润不小于模型(M1R-Cε)得到的利润, 即模型(M1R-Cε)δ的最优结果优于模型(M1R-Cε)的结果, 定理证毕。 基于上述分析和求解问题模型(M1R-Cε)δ或(M1C-Rε)σ的构建, 下面给出增广ε-约束方法求解模型(M1)的主要步骤, 具体流程图如图3中所示。 图3 增广ε-约束方法求解模型(M1)流程图 为了说明前面所建立模型(M1)能够给图1所示的供应链网络提供合理有效的产品订购,配送运输方案,使得整个供应链在满足顾客一定产品需求量的条件下能够同时达到成本与收益的最优,同时也为了进一步展现本文所设计的增广ε-约束方法优于标准的ε-约束方法,借助MATLAB数值计算平台,通过模拟数据和调用YALMIP[18]软件包中的分支定界算法BNB程序来求解相应的子问题模型。 为了尽可能多的满足顾客对产品的需求量,同时考虑到一些实际因素对顾客产品需求量的影响以及控制零售商的库存成本等,在数值测试的过程中,假设零售商对每种产品的订货量都不能超过或低于顾客需求量的50%,即γ=β=0.5。 表2 图1所示供应链中相关初始参数选取 图4 左图是模型(M1C)的最优方案决策结果, 右图是模型(M1R)的最优方案决策结果 图4中首先分别给出了模型(M1C)和(M1R)的最优解结果, 其中Cmin=1.5849e+5,R0=1.7523e+5,Rmax=2.2156e+5,C0=2.4315e+5, 这样就可以分别以Cmin和Rmax值为参考准则,选取合适的参数Cε≥Cmin和Rε≤Rmax来建立约束条件SUMC≥Cε和SUMR≤Rε。 同时又有模型(M1C)和(M1R)与模型(M1)具有相同的约束条件, 所以其相关最优解也是模型(M1)的某种有效解。 下图5中分别给出了使用模型(M1C-Rε)和(M1C-Rε)σ求解原模型(M1)而得到的最优决策方案结果, 其中参数Rε=1.5e+5,σ=1.0e-3, 模型(M1C-Rε)的最优值分别为SUMC=1.6137e+5,SUMR=1.8063e+5, 模型(M1C-Rε)σ的最优值结果分别是SUMC=1.5948e+5,SUMR=1.8019e+5。 通过简单的计算易知, 模型(M1C-Rε)σ相比较与(M1C-Rε)其成本SUMC相对下降率为(1.6137e+5-1.5948e+5)/(1.6137e+5)=1.17%, 而收益SUMR的相对下降率为(1.8063e+5-1.8019e+5)/(1.8063e+5)=0.24%。 很显然, 0.24%/1.17%=0.21,即收益的降低率仅约为成本降低率的五分之一, 所以从供应链整体利润的角度来说, 在当前决策方案下供应链是盈利的, 其利润相当于增加了五分之四。 所以, 模型(M1C-Rε)σ给出的最优方案要优于模型(M1C-Rε)的结果, 进而也说明了本文所设计的增广ε-约束方法优于标准的ε-约束方法。 图5 左图是模型(M1C-Rε)的最优决策结果,右图是模型(M1C-Rε)σ的最优决策结果 同理,下图6中又分别给出了模型(M1R-Cε)和(M1R-Cε)δ的最优决策方案结果,其中参数Cε=9.0e+5,δ=1.0e-5.模型(M1R-Cε)的最优值是SUMC=2.4264e+5,SUMR=2.2165e+5,模型(M1R-Cε)δ的最优结果是SUMC=2.3396e+5,SUMR=2.2165e+5。 值得注意的是,此两个模型得到的收益最优值都为2.2165e+5,等于最大收益值Rmax。这也说明了当使用模型(M1R-Cε)和(M1R-Cε)δ来求解原模型(M1)时,总能够在保证供应链整体收益最大的条件下来优化成本。模型(M1R-Cε)的最优成本为SUMC=2.4264e+5,而模型(M1R-Cε)δ的最优成本是SUMC=2.3396e+5,要低于模型(M1R-Cε)的成本,且成本相对下降率为(2.4262e+5-2.3396e+5)/2.4264e+5=3.75%。综上可得, 在保证收益相同且最大的条件下, 模型(M1R-Cε)δ的成本要低于模型(M1R-Cε)的成本,所以模型(M1R-Cε)δ给出的决策方案较好,这也进一步从数值的角度证明了本文的方法优于传统的ε-约束方法。 为了进一步具体比较分别使用模型(M1C-Rε), (M1C-Rε)σ和模型(M1R-Cε), (M1R-Cε)δ求解原问题时, 相关成本和收益值在供应链中各节点成员处的分配与变化情况, 其相关数值结果如下表3中所示。 数值结果表明, 相比较与模型(M1C-Rε)的结果, 模型(M1C-Rε)σ有效的降低了供应链中生产商和零售商的成本, 尽管生产商的成本有所增加, 但其还是降低了整个供应链的总成本。 对于各节点成员的收益而言, 模型(M1C-Rε)σ对生产商的收益有所降低,其他部分收益保持不变, 同时由于成本的降低幅度要远大于收益的降低情况, 所以从供应链整体来说其相关利润是潜在增加的。 同理,对比模型(M1R-Cε)和模型(M1R-Cε)δ的结果可知, 在模型(M1R-Cε)δ的决策方案下, 供应链整体亦具有潜在的利润增加。 同时, 为了更加直观的表现表3中的数据结果, 我们将其中的数据整理绘制成图7中所示的曲线图。 图6 左图是模型(M1R-Cε)的最优决策结果,右图是模型(M1R-Cε)δ的最优决策结果 表3 增广ε-约束方法与ε-约束方法分别求解时供应链中各节点成员最优成本与收益对比 图7 表3中数据结构曲线图 综合上述数据结果的对比分析可得,本文所建立的模型(M1C-Rε)σ和(M1R-Cε)δ,以及所设计的相关增广ε-约束方法是有效的,能够为图1所示的短生命周期产品供应链网络提供可行有效的决策方案。 针对短生命周期乳制品的特殊生产, 配送运输与销售等特点,本文研究了由供应商-生产商-配送中心-零售商所构成的四级供应链网络的成本与收益优化问题。 首先, 为了有效刻画产品在零售商处的实际库存水平,本文引入了一个新的非线性函数来定义产品的实时库存量。 在满足顾客一定产品需求量的条件了,建立了使得供应链中总成本和总收益能够同时最优的双目标非线性混合整数规划模型。其次, 基于模型的结构特点, 设计了一个新的增广ε-约束方法求解该优化模型。 数值结果表明,本文所建立的模型不仅能够为短生命周期乳制品供应链提供整体的成本与收益最优决策方案,而且所设计的方法要优于标准的ε-约束方法。相关研究成果对于研究设计供应链网络结构, 产品库存水平度量, 以及提升顾客满意度等都具有重要的潜在指导意义。 [1]QianGuixia,ZhangYipin,WuJianguo,et.al.Revenuesharingindairyindustrysupplychain-AcasestudyofHohhot,China[J].JournalofIntegrativeAgriculture, 2013, 12(12): 2300-2309. [2] 吴继贵, 叶阿忠.FMCG供应链风险综合评价研究——以中国乳制品供应链为例[J]. 科技管理研究, 2014,34(22): 43-49. [3]BilgenB,CelebiY.Integratedproductionschedulinganddistributionplanningindairysupplychainbyhybridmodeling[J].AnnalsofOperationsResearch, 2013, 211(1): 55-82. [4]NicholsonCF,GomezMI,GaoOH.Thecostsofincreasedlocalizationforamultiple-productfoodsupplychain:DairyintheUnitedStates[J].FoodPolicy, 2011, 36(2): 300-310. [5]SelC,BilgenB,Bloemhof-RuwaardJM,et.al.Multi-bucketoptimizationforintegratedplanningandschedulingintheperishabledairysupplychain[J].Computers&ChemicalEngineering, 2015, 77(9): 59-73. [6]XuJiuping,YaoLiming,ZhaoXiaodan.Amulti-objectivechance-constrainednetworkoptimalmodelwithrandomfuzzycoefficientsanditsapplicationtologisticsdistributioncenterlocationproblem[J].FuzzyOptimizationandDecisionMaking, 2011, 10(3): 255-285. [7]ChenXin,PangZhan,PanLimeng.Coordinatinginventorycontrolandpricingstrategiesforperishableproducts[J].OperationsResearch, 2014, 62(2): 284-300. [8] 李贵萍, 段永瑞, 霍佳震,等.持有成本和变质率时变的非立即变质品库存策略[J]. 中国管理科学, 2015,23(8): 122-131. [9] 徐贤浩, 蔡成元, 沈古文.基于可控提前期和延迟供货的短生命周期产品库存模型[J]. 中国管理科学, 2010, 18(2): 42-47. [10] 陈芳, 单而芳, 郭传好. 匹配理论下乳制品供应链网络设计与成本优化研究[J].中国管理科学, 2015,23(S1): 610-616. [11]AyagZ,SamanliogluF,BuyukozkanG.AfuzzyQFDapproachtodeterminesupplychainmanagementstrategiesinthedairyindustry[J].JournalofIntelligentManufacturing, 2013, 24(6): 1111-1122. [12]ManikasI,ManosB.Designofanintegratedsupplychainmodelforsupportingtraceabilityofdairyproducts[J].InternationalJournalofDairyTechnology, 2009, 62(1): 126-138. [13]MioriV,SegulinBW.Applicationoftripletnotationanddynamicprogrammingtosingle-line,multi-productdairyproductionscheduling[J].InternationalJournalofBusinessIntelligenceResearch, 2010, 1(2): 9-20. [14] 杨亚, 范体军, 张磊. 新鲜度信息不对称下生鲜农产品供应链协调[J].中国管理科学, 2016,24(9): 147-155. [15] 赵忠, 王淑云, 李波. 时变需求下基于两级信用支付的易腐品订货模型[J].系统管理学报, 2016,25(1): 83-89. [16]EhrgottM,GandibleuxX.Multiobjectivecombinatorialoptimization-theory,methodology,andapplications[M]. //EhrgottM,GandibleuxX.Multiplecriteriaoptimization:Stateoftheartannotatedbibliographicsurveys,Holland:KluwerAcademicPublishers, 2002: 369-444. [17]MiettinenKM.Nonlinearmultiobjectiveoptimization[M].Holland:KluwerAcademicPublishers, 1999. [18]L"{o}fbergJ.YALMIP:AtoolboxformodelingandoptimizationinMATLAB[C]//ProceedingsoftheCACSDConference.Taipei,Taiwan,September2-4,2004. CostandRevenueOptimizationforSupplyChainNetworkofDairyProductswithShort-Life-Cycle GUO Chuan-hao1, CHEN Fang2, SHAN Er-fang3 (1.School of Economics andManagement, Zhejiang Sci-Tech University, Hangzhou 310018,China;2.Information and Supply Chain Services, SinopharmLogistics Co.,Ltd, Shanghai 200443,China;3.School of Management, Shanghai University, Shanghai 200444,China) Compared with the developed countries, the cold chain logistics started relatively late in China. Nowadays, there still exists some problems in cold chain logistics in China. For instance, facilities are not complete, cold chain management is not perfect, cost is high, profits are low, and so on. Especially, the supply chain network of dairy products with short-life-cycle is a special class of cold chain logistics. Since the dairy products with short-life-cycle are perishable, we need not only to make sure of the quality of dairy products, but also to send them to the right place in the fastest way, in the shortest possible time. Meanwhile, the dairy products with short-life-cycle have some characteristics. For example, the customer demand is uncertain and difficult to predict, product variety, the small amount of product′s order, etc. Thus, the requirements for dairy products supply chain network management are higher, and subsequently, the corresponding cost is relatively high.One of the goals of researches on supply chain network is to minimize the total cost and maximize the total revenue at the same time under the condition of the whole supply chain network satisfying the customers certain demand. In this paper, for short-life-cycle dairy products which have many varieties and are difficult to store as well as have some special requirements in the process of transportation, the related cost and revenue optimization problems for the four levels of dairy products supply chain network with ''supplier-manufacture-distributioncenter-retailer" are studied. Under the condition of satisfying the customers demand for some products, a double-objective mixed-integer programming model is established, which can ensure that the cost and the revenue of the dairy products supply chain network could obtain the optimal value at the same time. Moreover, in order to describe the product′s practical inventory for retailers effectively, a new nonlinear function is introduced in this paper to define the dairy product′s inventory. By making use of the structure characteristics of the proposed model, a new augmentedε-constraintmethodisdesignedtosolvethemodel.Theempiricalanalysisresultsshowthattheproposedmodelcouldnotonlyprovideoptimaldecision-makingschemesuchthatthecostandtherevenueofthewholesupplychainnetworkcouldachievetheoptimalvalueatthesametime,alsogivetherelatedoptimaldecisionschemesfortheproductsproduction,transportationandsoon.Furthermore,thedesignedmethodismorepromisingthanthestandardε-constraintmethod.Therelatedresearchresultshaveimportantpotentialguidingsignificanceforstudyinghowtooptimizethecostandtherevenueofsupplychainandimprovethecustomer′ssatisfaction,solvingthegeneraldouble-objectiveoptimizationproblemsandsoon. supply chain network; cost optimization; revenue optimization; double-objective mixed-integer programming; augmentedε-constraintmethod 1003-207(2017)02-0087-11 10.16381/j.cnki.issn1003-207x.2017.02.010 2015-09-13; 2016-05-24 国家自然科学基金资助项目(11501350, 11501351, 71572104); 浙江理工大学科研启动基金项目(16092098-Y) 郭传好(1980-), 男(汉族), 安徽滁州人, 浙江理工大学经济管理学院, 讲师(特聘教授), 研究方向: 供应链管理与优化,E-mail:guo-ch@163.com. C935;F253;F A

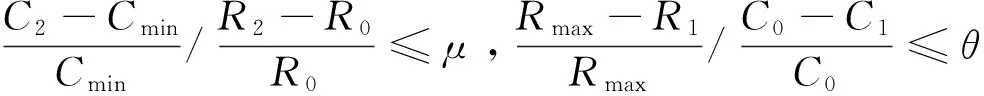
4 实证结果分析
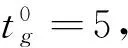



5 结语

