基于高维动态藤Copula的汇率组合风险分析
韩 超,严太华
(重庆大学经济与工商管理学院,重庆 400044)
基于高维动态藤Copula的汇率组合风险分析
韩 超,严太华
(重庆大学经济与工商管理学院,重庆 400044)
以Pair Copula为简单构造模块的高维动态藤Copula结构能够克服二元Copula面临的“维度诅咒”问题,对多元变量之间的非线性相依进行动态化描述,是Copula函数研究的学术前沿。本文选取美元、欧元、日元、港币及英镑五种汇率的日间对数收益率数据实证研究,对其进行AR-GJR-GARCH模型过滤,过滤所得新息序列用GPD模型拟合,之后进行概率积分变换,采用高维动态C藤和D藤Copula对变换后序列建模,运用蒙特卡罗方法计算组合风险VaR,对其进行UC回溯测试,并与相应的静态方法作比较。结果表明:高维动态C藤Copula结构计算出来的VaR表现最好,对其进行分解发现美元的边际风险最低,通过蒙特卡罗选择权重组合发现最大限度持有美元将会产生最小VaR。该结论为量化风险指标、合理配置资产,及风险监管提供了一种新的模型与方法。
AR-GJR-GARCH模型;高维动态藤Copula;汇率组合风险;VaR;UC回溯测试
1 引言
1973年,以“双挂钩”形式为特征的布雷顿森林体系终究因为“特里芬两难”积重难返而瓦解,其后,浮动汇率体制大行其道。浮动汇率制在使各国获得“不可能三角”另外两极的同时,也加剧了国际贸易与国际金融的汇率风险,国际间的风险传染变得难以计量和掌控,汇率风险也因此成为学术领域的研究热点。
在汇率风险研究中,单一维度的汇率风险计量并不能适应存在错综复杂关系国际汇率间的内在要求,传统的以线性相关为基础的二维或者多维汇率组合风险计量又无法真实把握汇率风险之间的非线性相依和时变相依特征。基于此,许多学者开展了相关的研究,其中以二元或者多元Copula函数为研究方法的文献较为常见,比如:吴振翔等[1],Patton[2],柏满迎和孙禄杰[3],苟红军等[4]。
然而,传统的二元Copula函数会面临“维度诅咒”问题,传统的多元Copula函数又会因为只能采用同一种Copula的某一两个参数去描述多元变量之间的复杂相依关系而受到限制。为了突破这种局限,学者们开始了Copula函数高维化和动态化的前沿研究,其中,高维动态藤Copula以Pair Copula为简单构造模块,能够弥补传统二元或者多元Copula的缺陷,对多元变量之间的非线性相依关系进行灵活地动态化描述,相关的研究有:So和Yeung[5],Reboredoa和Andrea[6],叶五一等[7],杜子平等[8]。
鉴于以上,本文运用最新的高维动态藤Copula方法研究汇率组合风险问题。研究中采用AR-GJR-GARCH模型对原始序列进行过滤,对过滤所得新息序列用GPD模型进行概率积分变换(PIT),之后运用高维动态藤Copula进行多元动态相依建模。在理论分析的基础上,选取美元、欧元、日元、港币及英镑五种汇率的日间对数收益率数据为研究对象,对其进行边际分布和相关性结构的拟合与检验,运用蒙特卡罗模拟方法对动态和静态情形进行比较,最后进行VaR的边际风险和最小VaR的资产组合权重研究。研究结论对于投资决策、风险管理和风险资本配置等具有参考意义。
2 理论基础
2.1 藤Copula基本理论
根据Sklar[9]的定义,Copula本质上是描述变量的连接函数。在给定信息集F[t-1]时,rit,i=1,2,…,p的条件联合累积分布及其密度函数可以分别表示为式(1)(2):
(1)
(2)

式(2)借助于藤结构形式可以分解成一系列的二维Copula,以规则藤中最常见的C藤和D藤为例,二者的p维密度函数可以分别表示为式(3)(4):
(3)

(4)
式(1)-式(4)中的Copula及C藤和D藤Copula函数可以用边际分布与Copula联合表达,二者建模可以分离进行,计算上更为可行,称之为“两阶段建模”。“两阶段建模”为进一步利用藤Copula对多维风险变量的组合风险计量提供了可能,本文借助于C藤和D藤Copula方法开展汇率组合风险研究。
2.2 高维动态藤Copula构建
高维动态藤Copula的构建需要进行藤的类型选择。以规则藤中最常见的C藤和D藤为例,二者的类型选择取决于多维变量之间有无关键变量,也就是与其他变量之间的相关关系是否压倒性的超过其他变量之间的关系。C藤或D藤确定以后,需要进行藤的排列,第一棵树的排列尤为重要,它决定了之后树的结点和边的构造。对于第一棵树,C藤需要将关键变量置于根部,其余变量按照与根部的紧密关系依次排列;D藤也面临着变量之间相关强度大小的问题,依据相关度大小排列成对变量,据以构成树形图,需要注意的是D藤中当一个变量被选择两次的时候,它不能在第一棵树上形成新的Pair Copula对。按照规则藤的定义,无论C藤还是D藤,树j的边是树j+1的结点,树j的边的数量与树j+1结点的数目相同,树j拥有共同节点的两条边在树j+1上是相连的,第一棵树确定了,其余树的顺序也就依次得出了。
藤的类型与排列确定以后,就进入了藤的拟合阶段。由式(3)(4),C藤和D藤的构建过程中条件分布函数F[t]起到了关键作用。对于C藤和D藤来说,F[t]的计算方式有很大差异,分别为式(5)、式(6):
(5)
(6)
这种差异使得同样的F[t]函数表达式,C藤和D藤计算的最终结果将截然不同。本文主要以成对t-Copula研究高维动态藤Copula结构,其F[t]函数及参数都是时变的,可以表示为式(7):
(7)
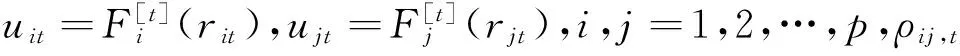
(8)
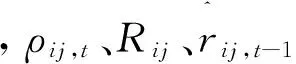
(9)
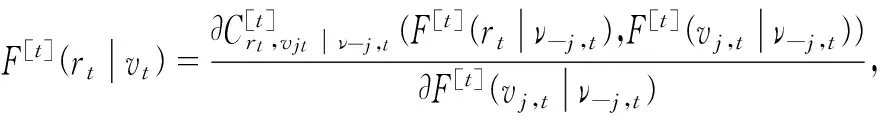
则式(9)就可以求出动态h函数值,其中vt表示时序t的随机向量,ν-j,t是剔除掉第j个变量的vt向量。
以动态h函数为中介函数,循环往复地求解藤Copula每棵树的参数,步骤如下:
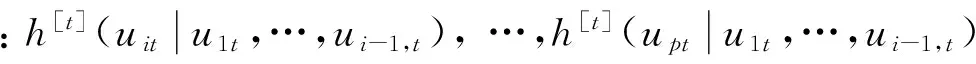
②从第二棵树开始,上一棵树的边即连接结点的Copula函数,采用动态t-copula,动态参数为动态表达式(8)的参数,根据动态h函数式(9)求得h序列,作为下一棵树的结点数据;
③直到最后一棵树,迭代运算步骤②,可以计算出每棵树上的h函数的参数及对应的动态化h序列,这就完成了整个藤的构建。
在形式上C藤结构较之D藤要复杂,其实,D藤无论是构建、拟合,还是仿真都比C藤复杂、困难,这源于二者的F[t]函数求解式(5)和式(6)的不同。
2.3 高维动态藤Copula仿真
C藤和D藤Copula结构的仿真算法形式上相同,以五维为例,都有式(10):
x1t=w1t

(10)
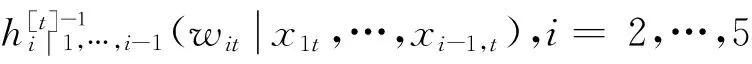
x1t=w1t
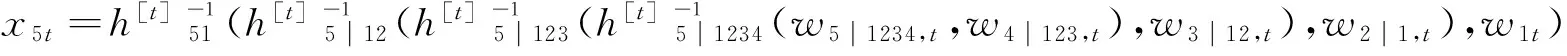
(11)
x1t=w1t
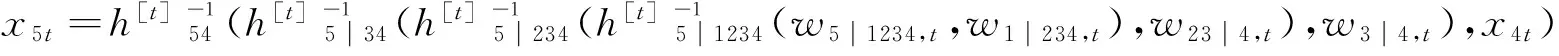
(12)
无论对于高维动态C藤还是D藤的数据仿真,计算过程都应该是动态化的,动态参数由相应的动态型h函数和时变Copula函数求得,动态参数服从式(8)中的动态演进式。为了更为直观的表达仿真计算过程,分别画出x5t在C藤和D藤中的仿真路径图,如图1和图2,其中C藤和D藤h逆函数的条件变量剔除次序是相反的。图中,W5为w5t的集合向量,X5为x5t的集合向量。

图1 动态C藤Copula的仿真路径图
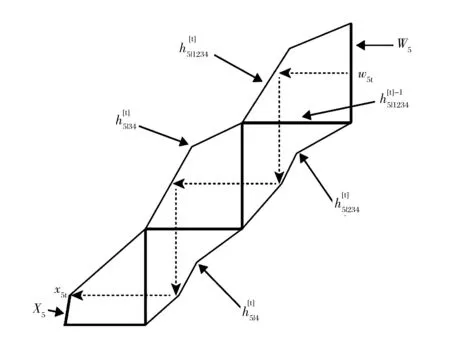
图2 动态D藤Copula的仿真路径图
2.4 VaR与回溯检验
VaR表示资产收益率序列在显著性水平α下的分位数。求解VaR有历史模拟法、方差-协方差方法和蒙特卡罗模拟法等。本文结合研究实际借助Matlab编程采用蒙特卡罗模拟方法,按照拟合的藤结构仿真多维数据,倒推出模拟收益率序列,每10000个数据模拟实现之后,通过计算机按照相应的显著性水平自动选择位于数据排序左端的对应数据作为此10000个数据组的1个VaR值,如此得出包含400个元素的VaR的随机序列组,将其与样本外400个数据分别进行返回检验,观察比较高维动态藤Copula与高维静态藤Copula的风险效果。VaR的这一回溯检验是通过R语言来编程实现的,理论基础是Kupiec[11]的UC检验。
3 计算路径与模型
本文采用两阶段建模方法拟合藤结构,通过h逆函数对藤Copula结构进行数据仿真,这一过程涉及到若干次建模与计算,计算路径可以分解为以下步骤:
①用AR-GJR-SkewT模型对多元收益率序列进行过滤,模型表示如式(13)所示:
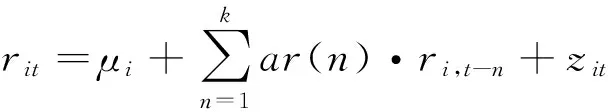
zit=σit·εit
εit~i.i.dST(λi,ηi)
(13)
其中λi,ηi分别表示SkewT分布的偏斜度和自由度。
②对①中的新息序列进行双尾GPD极值建模,模型如式(14)所示:
i=1,2,3,4,5
(14)
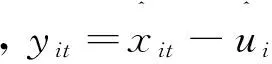
③对PIT序列进行动态PairCopula建模,求出相应的时变相关系数序列,对其求均值。这里主要采用的是Pair-t-Copula函数,模型表示为式(15)所示,其中,uit,ujt均表示成对PIT序列元素,令xt=(xit,xjt)′,则:
(15)
④比较高维PIT序列的两两相关系数均值,分析是否存在主导变量,以确定藤的类型和关键变量,如果存在主导变量,则采用C藤。
⑤分别以C藤和D藤作比较研究,拟合边和节点的参数,方法参照2.2节内容。
⑥根据⑤中藤Copula的动态参数仿真PIT序列,仿真过程中需要进行动态h逆函数的倒推与求解,对于t-Copula来说,h逆函数可以表示为式(16):
(16)
⑦对⑥中的动态仿真PIT序列按照②①的结构进行返回倒推,即可求出高维动态相关收益率序列。
⑧对动态收益率序列按2.4节蒙特卡罗方法计算VaR值,并且进行样本外返回检验。
⑨分析边际VaR,求解最小VaR的资产组合权重。
4 实证研究
4.1 数据预处理
本文以美元(USD)、港币(HKD)、欧元(EUR)、英镑(GBP)和日元(JPY)五种外汇为研究对象,时间区间从2007年1月4日到2015年8月25日,取日间对数收益率Ri,t=ln(Pi,t/Pi,t-1)为研究指标,其中,P表示汇率的中间价,i=1,2,3,4,5,分别表示USD、EUR、JPY、HKD和GBP五种外汇,共2102组数据。前1702组五维数据为样本内数据,用来模型拟合,后400组数据用来进行VaR的样本外返回检验。全文数据建模与分析借助于Matlab、R语言、SPSS等软件实现,数据取自中国货币网的外汇中间牌价。表1为五维序列的特征统计表,显见五维数据的尖峰厚尾性,Jarque-Bera统计量强烈拒绝正态性假定,同时数据分布具有左偏特性。
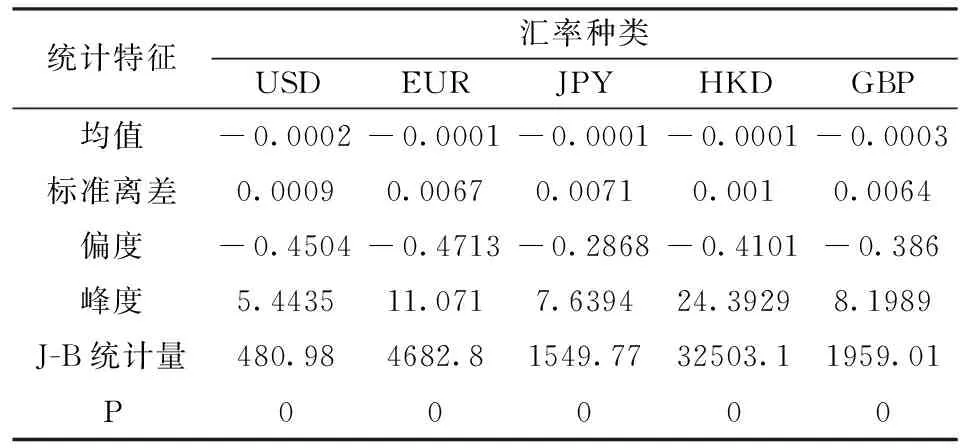
表1 五维汇率收益率特征统计表
4.2 平稳性检验
平稳性是金融时间序列建模和预测的前提,本文运用模型对数据进行过滤之前必需对数据进行平稳性检验,相应的单位根ADF检验结果如表2所示,可见五种金融时间序列的ADF值都远远突破了1%、5%、10%显著性水平的临界值,均强烈拒绝单位根存在的原假设,没有理由认为五种金融时间序列不是平稳时间序列。
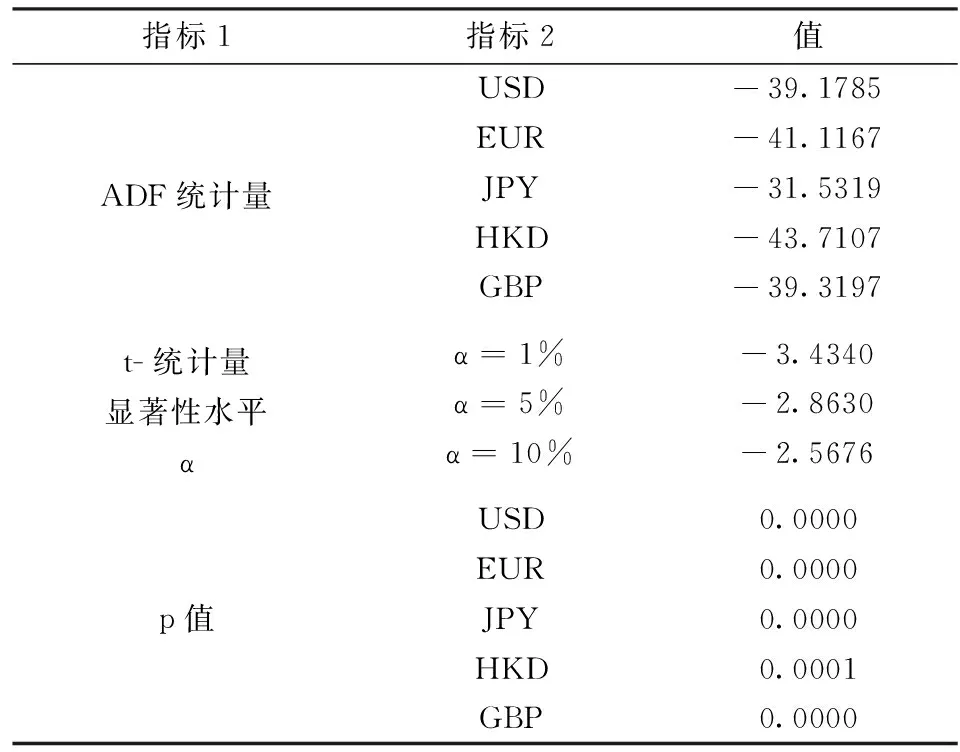
表2 日对数汇率收益率平稳性检验表
4.3 独立性检验与波动性聚类判别
Brock、Dechert和Scheinkman[12]基于关联积分的定义提出了BDS检验统计量,并且证明在独立同分布的原假设下该统计量满足渐近的标准正态分布。基于此,本文采用BDS检验方法检验五种金融时间序列的独立同分布特征,检验结果表明,五种金融收益率序列BDS检验的p值均为0,拒绝了独立同分布原假设,需要进一步的数据处理。为了进一步检验并且证实这一点本文接下来进行原始序列和平方序列的自相关检验。以美元(USD)和欧元(EUR)为例,绘制自相关图3和图4。从图中可以发现轻微程度的序列相关和波动持久记忆特征,说明存在GARCH效应,4.4.1节中采用AR-GJR-GARCH模型消除这一特征,取得了较好的效果。
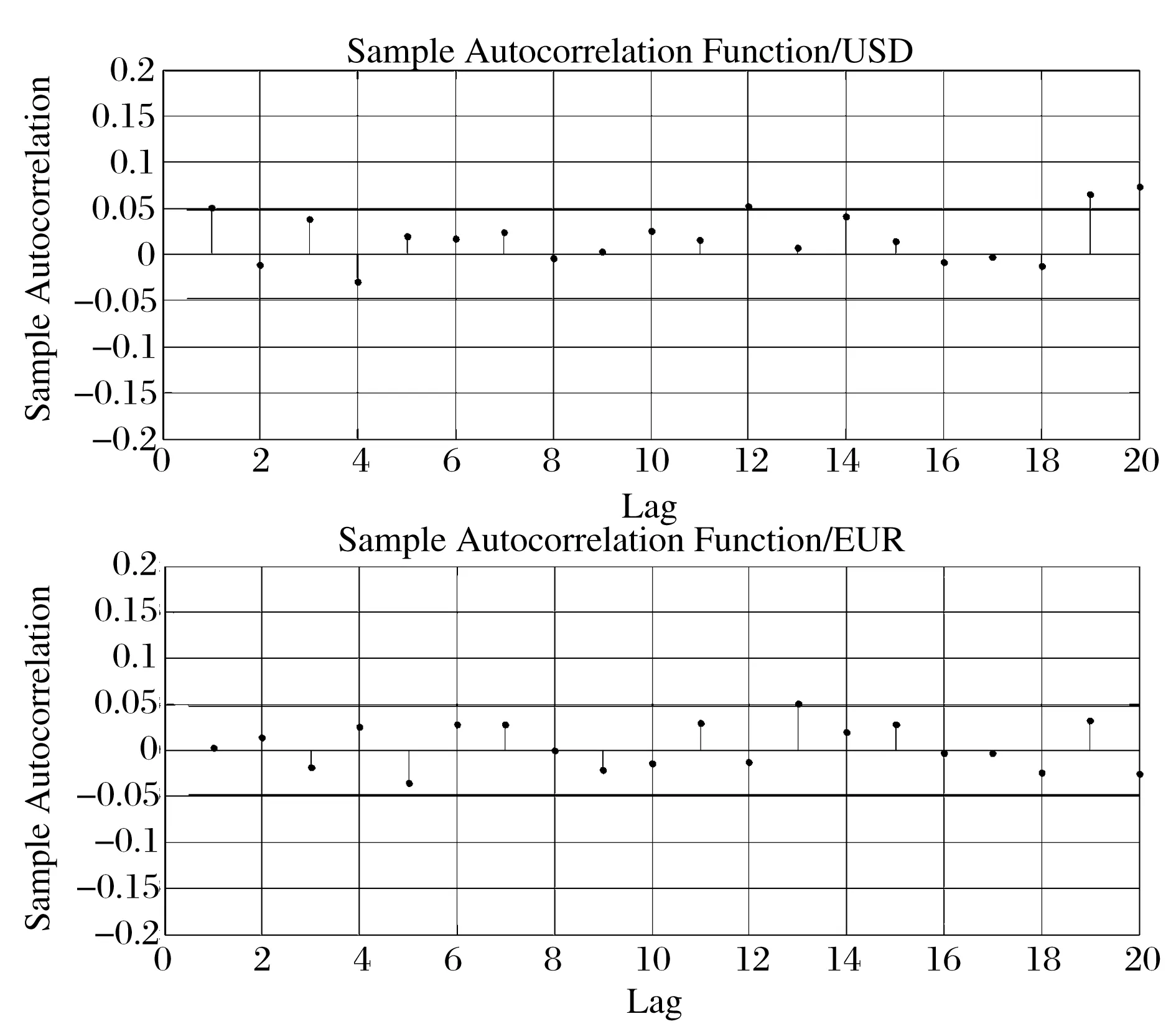
图3 汇率收益率的自相关图
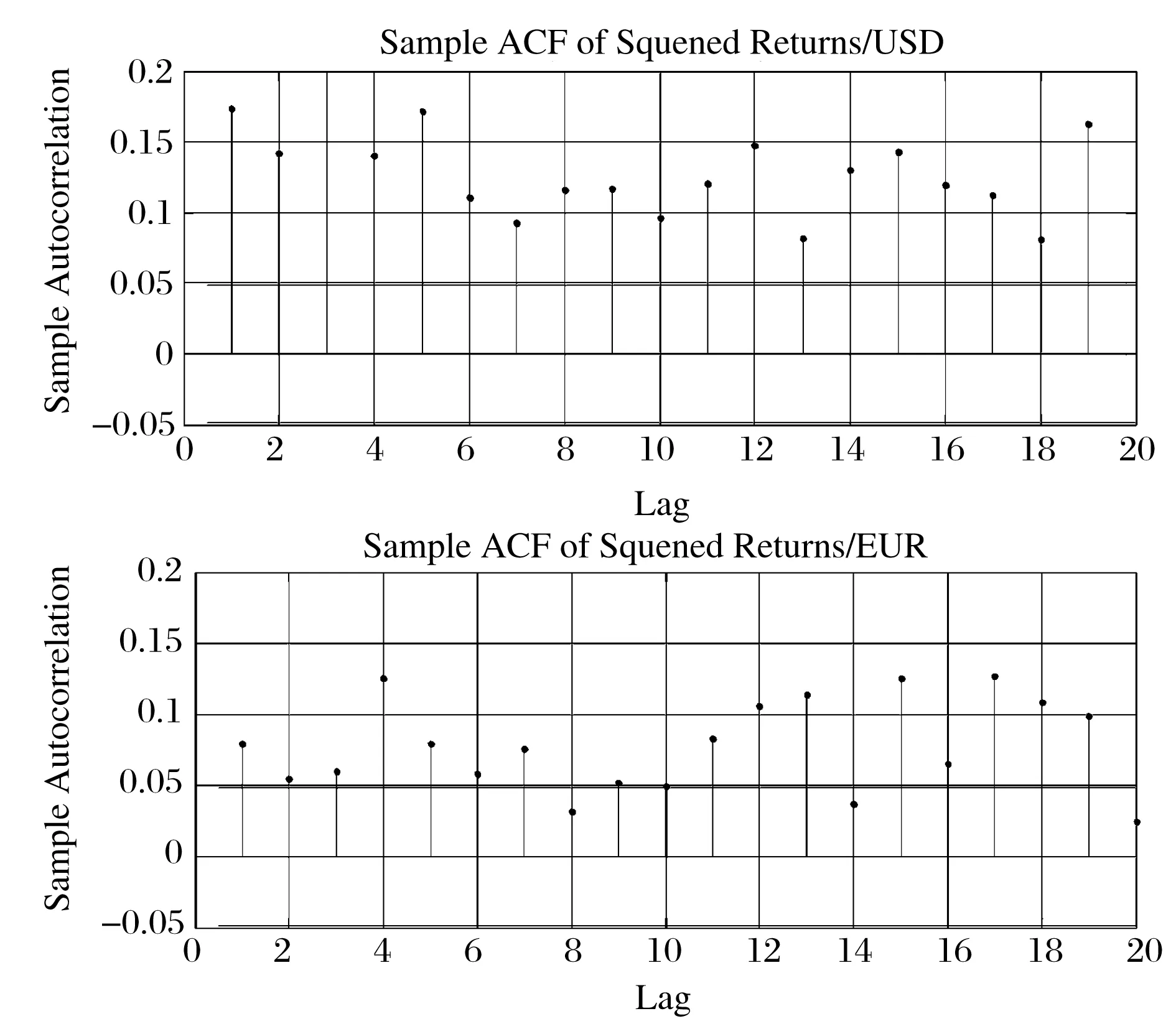
图4 汇率收益率的平方自相关图
4.4 单个时间序列的模型提炼与数据过滤
McNeil等[13]的研究表明:如果金融时间序列非独立,但满足平稳性条件,在一定的弱相依条件下,仍然可以应用极值模型,若要采用极值模型则要求大致符合独立同分布条件。但以上检验结果表明:五种汇率收益率序列均具有平稳性但不具独立性,有轻微的序列相关性和偏斜特征,存在GARCH效应。因此,本文采用AR-GJR-GARCH模型,通过标准化残差过滤数据,生成大致符合独立同分布的新息序列。
4.4.1 单个时间序列的模型提炼
本文采用AR-GJR-GARCH模型来对单个时间序列进行拟合。其中,AR模型用来消除单个金融序列的自相关,阶数根据实际有所不同,GJR模型用来克服收益率序列的波动性聚类和正负新息冲击的非对称性特征,而偏斜t(Skew T)分布能够准确描述序列的尖峰、厚尾和偏斜特性,解决模型过滤后标准化残差分布存在的偏斜问题。
采用AR-GJR-GARCH模型对五维时间序列进行数据过滤,生成相应的新息序列。对过滤所得的标准残差序列分别绘制自相关图和波动性聚类图,以验证模型的实际效果,仍以美元(USD)和欧元(EUR)为例,相应的自相关检验和平方自相关检验结果见图5和图6,经过与数据过滤前的原始序列及平方序列的自相关图相比较,可以发现数据过滤消除了大部分自相关现象,对其进行BDS检验,在5%的显著性水平下,五维序列也大致都能接受序列符合独立同分布的原假设。这样,过滤后的数据就基本达到了后续尾部极值拟合所要求的预定效果。
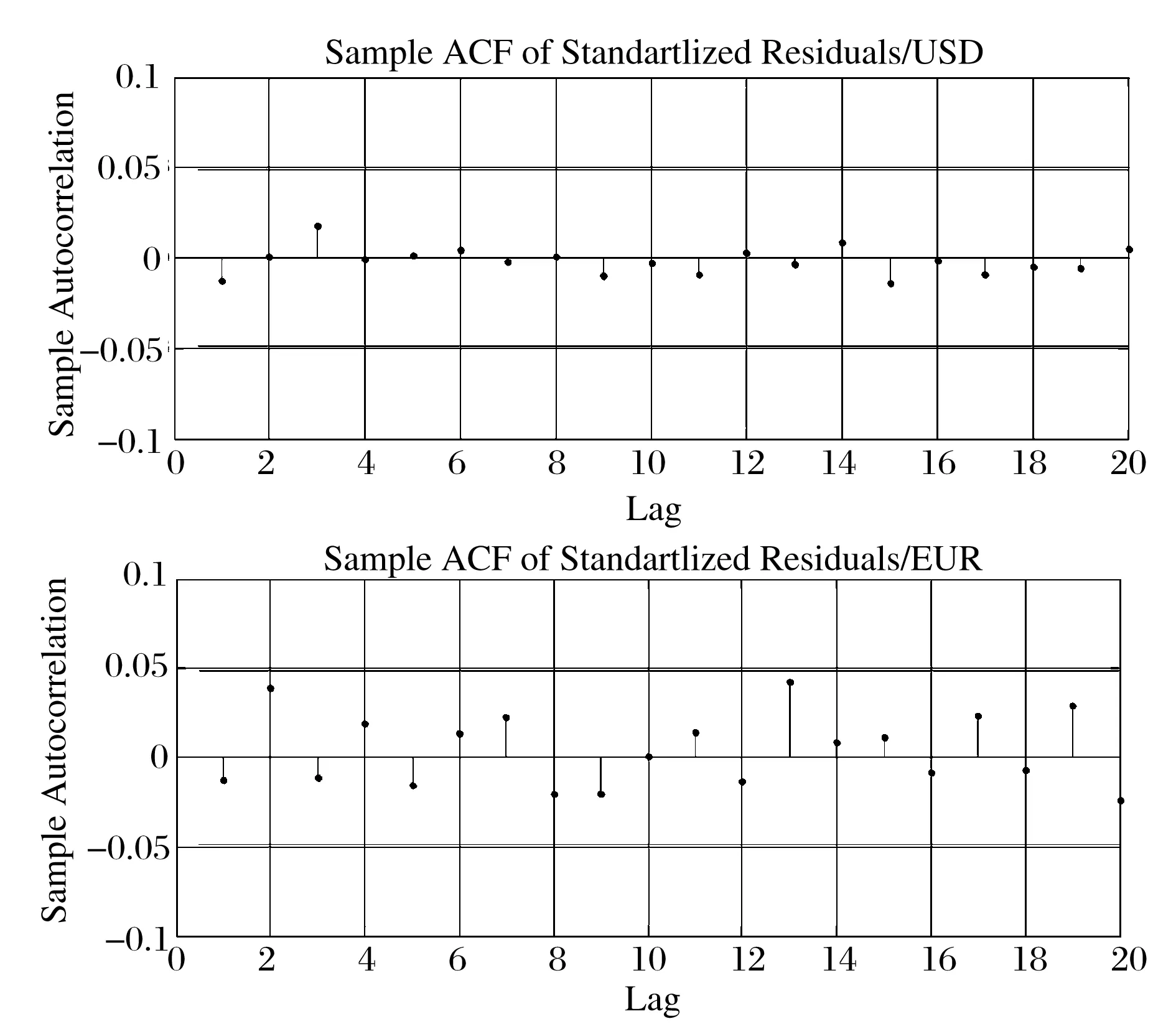
图5 新息序列的自相关图

图6 新息序列的平方自相关图
4.4.2 广义帕累托分布(GPD)参数估计与拟合检验
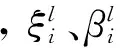
4.5 高维动态藤Copula的参数估计
4.5.1 高维动态藤Copula的类型选择
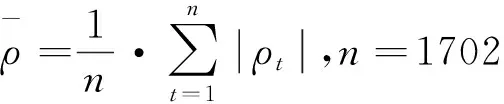

表3 GPD拟合参数及PIT检验表

表4 静态t Copula函数两两相关比较表

表5 动态归一化两两相关比较表
经过静态和动态的两两相关比较可以发现,没有任何一个变量能够处于绝对的强势地位,如USD在与JPY和HKD的相关性上大于其余几种外汇与JPY和HKD的相关性,而与EUR的相关性却小于GBP,与GBP的相关性小于EUR,从这个角度来说,采用D藤拟合是合适的;然而进一步比较又可以发现美元(USD)处于相对主导地位,比如USD与EUR的比较,尽管USD与GBP的关系小于EUR与GBP,但是USD与JPY和HKD的相关均大于EUR与JPY和HKD的相关,类似的方法进行比较可以得出USD处于相对主导地位的结论,从这个角度来说,似乎采用C藤也可行。本文出于典型研究需要,分别采用C藤和D藤进行比较研究,得出二者中更为合适的类型,而对介于C藤和D藤之间的别的结构形式不予考虑。
完成以上的工作后,接着进行藤Copula的排列。由表4和表5可以比较得出第一棵树的变量排序:USD、HKD、EUR、GBP、JPY。按照2.2节中的排列方法可以分别绘制出C藤和D藤的结构图7和图8。其中,数字1,2,3,4,5分别表示USD、EUR、JPY、HKD和GBP五种外汇汇率,Tj,j=1,2,3,4分别表示藤的第j棵树,树的数目比维度少1。
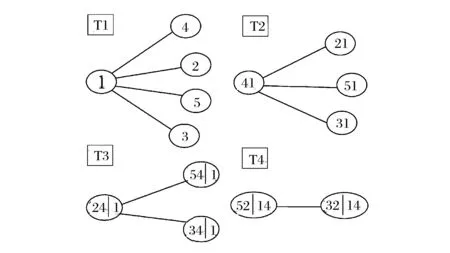
图7 五维C藤排序结构图
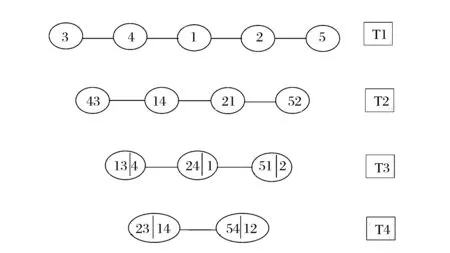
图8 五维D藤排序结构图
4.5.2 高维动态C藤和D藤Copula的拟合
高维动态C藤和D藤Copula是许多高维静态C藤和D藤Copula的集合体,对于tCopula函数而言,假定相关参数是时变的,而自由度保持不变,按照2.2节的构建方法,借助于Matlab编程就可以得到以h函数为构成要素的动态C藤和D藤Copula函数的参数,如表6和表7所示。

表6 高维动态C藤Copula函数参数表
注:vij表示tCopula的自由度,αij、βij分别表示动态方程式(8)中的对应参数;此表的h41和表7的h14参数相同,序列却不同,原因在式(9)。

表7 高维动态D藤Copula函数参数表
注:因为拟合t Copula的自由度大于30,根据相关理论,Gaussian-Copula是t-Copula自由度很大时的特例,因此,的空格所在的h函数对应的参数以Gaussian-Copula函数来拟合,此时自由度vij即为空值,有关Gaussian-Copula的理论参见韦艳华[16]。
4.6 高维动态C藤和D藤Copula函数的仿真与VaR测度
按照4.5节中藤的结构和第3节的仿真方法进行数据仿真,分别以1%,5%和10%的显著性水平,蒙特卡罗模拟得到相应的VaR值序列,然后对其进行样本外返回检验,比较不同方法对于组合风险VaR计算的准确性。为了使研究更具有一般意义,本文随机选取两种组合比例分别为(20%,20%,20%,20%,20%)与(10%,30%,20%,10%,30%),所产生的对应的组合风险序列分别为VaR1和VaR2。按照前述方法进行仿真,求得1%,5%,10%显著性水平两种比例的VaR序列,与相应的样本外数据比较,再运用Kupiec Test方法进行回溯检验,得到无条件覆盖(UC)检验结论,结果如表8所示。
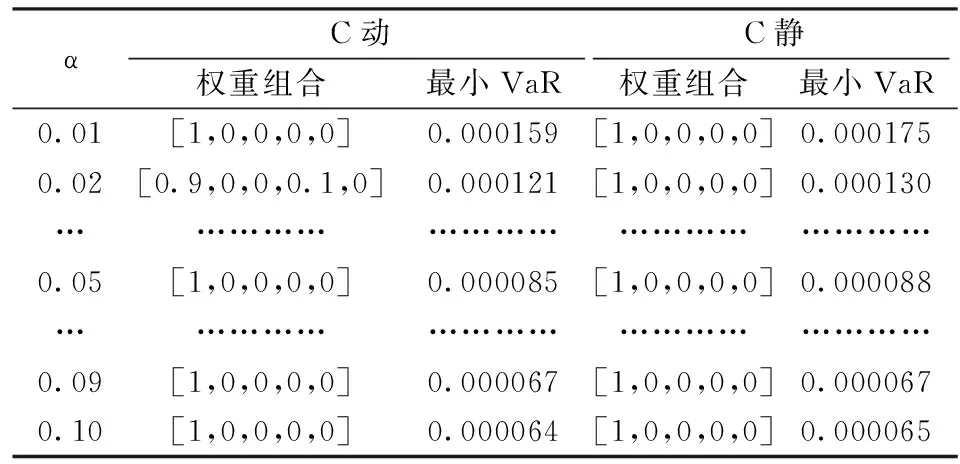
为了表述方便,我们把高维动态C藤简称为C动,其余类似推之。经过比较可以发现对于VaR1而言,10%的显著性水平上,接受概率C静 表8 藤Copula回溯检验统计量表 值得注意的是,D动在每次检验中实际超越都不同程度的大于期望超越,甚至在5%显著性水平下VaR1拒绝了原假设,这可能因为:在4.5.1节中首先进行的是藤的类型判定,为了研究更具典型性,从C藤和D藤两种规则藤类型中选择,经过相关分析,尝试性的分别采用C藤和D藤进行比较研究。而实际上结合国际货币制度的迁延史,自从二战后布雷顿森林体系以双挂钩的形式确立美元霸主地位以来,尽管美元的国际地位有所下降,直到当前仍是国际主要通用支付工具,美元相较于欧元、日元、港币及英镑,无疑是关键变量。而本文的研究进一步佐证了这一点,说明采用以美元汇率为关键变量的C藤Copula更为合适:表8中D动的表现则说明采用C藤比D藤更好,D动表现弱于D静,说明如果模型选择不准确,改进模型可能就会在错误方向上走得更远;而表6的拟合效果明显优于表7,尤其是第三棵树和第四棵树的参数显著性水平与对数似然值,辅助说明了C藤更为占优。 以上分析说明:藤Copula用来风险计量时需要进行优化选择,只有采用正确的模型种类,建模的分析效果才会更加准确。进一步从表8中可以发现:总体上C动模型最优,且C动在5%和1%的显著性水平下有过两次概率为1的完美风险捕捉;C动优于C静也验证了动态模型由于更为精准的刻画风险之间的时变相关而优于静态模型。 风险管理实践中,仅仅对于组合风险进行计量是不够的,还必须了解投资风险的内部构成、不同的组合权重VaR有何区别,及最小VaR所对应的权重组合。为此,本节内容从VaR的分解与VaR的资产组合权重两个角度对高维动态C藤和静态C藤Copula结构计量的外汇组合风险作进一步的研究。 5.1 VaR的分解 Hallerbach[17]系统研究了M-VaR(边际VaR)、C-VaR(成分VaR)、I-VaR(增量VaR)的相关理论,指出C-VaR和I-VaR的求解可以通过M-VaR得到。因此,研究M-VaR有着特殊的意义。根据杜红军、胡海鹏、邵欣炜等[18-20]的研究,在正态分布假设下,组合期望回报为零时,有: 其中,VaR(P)为组合风险,wi为第i种资产权重。按照这种计算方法,结合本文的研究实际,可以分别求出等权重和不等权重两种风险的VaR1和VaR2的边际风险,对其进行分析,认为:三种显著性水平的C动和C静都分别有USD的M-VaR最低,HKD次之,EUR的M-VaR最高,说明在追求更小VaR的过程中,文中的两种资产组合都应该增加USD,减持EUR等资产。但是这种判断方法只能判断局部的投资组合倾向,无法给出全局的最优比例,为了得到最小VaR对应的最优资产权重组合,我们在5.2节中采用蒙特卡罗模拟进行全局最优选择。 5.2 最小VaR的资产组合权重 吴振翔等[1]基于静态Archimedean Copula函数运用方差-协方差方法确定了二维汇率组合风险最小VaR的投资组合,对于本文具有一定的启示意义。不同的是,本文采用高维藤Copula方法蒙特卡罗模拟出静态与动态的外汇组合风险VaR,通过对不同组合比例的VaR进行比较,发现最小VaR对应的权重组合,得出不同的分析结论。 本文进行VaR的资产组合权重分析,将会面临资产组合选择过多的问题。为了使研究更具可行性,假定五维外汇资产USD、EUR、JPY、HKD和GBP在组合中的资产权重分别为j,k,l,m,n,资产权重的选择分别以0.1为步长,在0≤j,k,l,m,n≤1,j+k+l+m+n=1,且资产权重均为0.1整数倍的约束下,每10000次的仿真将会面临: 次不同权重组合的VaR计算,然后对每1001次的VaR进行比较,找出给定显著性水平α下的最小VaR及对应的资产权重组合。表9是在不同的显著性水平下,分别在1001个VaR中找到最小VaR值和对应资产组合权重的结果,表明无论C动或者C静,几乎都主张将资产全部放在美元上,这与我们的经验也是相符的:美元是低风险的外汇资产。 表9 不同α下的最优权重组合 本文以市场风险中的汇率风险为研究对象,针对汇率风险因子之间可能存在的非线性相依情形,首先对高维时间序列进行AR-GJR-GARCH模型过滤,对过滤所得新息序列用GPD模型拟合,以拟合所得参数对五维新息序列概率积分变换,得到五维PIT序列。然后分别进行C藤和D藤的静态和动态Copula拟合,按照拟合参数进行五维数据仿真,再依据过滤模型进行数据倒推,得出仿真收益率数据,按照两种投资组合比例和三种显著性水平分别得到包含400个元素的VaR值序列,对其进行UC回溯测试,发现高维动态C藤Copula结构表现最好,更适合汇率组合风险计量。最后结合M-VaR和蒙特卡罗方法研究了最小VaR对应的资产权重组合,发现最大限度持有美元将会有效降低风险VaR值。 论文所作的研究为投资决策、风险管理和风险资本配置及风险监管提供了一种新的计算思路与计量方法。 [1] 吴振翔,叶五一,缪柏其.基于Copula的外汇投资组合风险分析[J].中国管理科学,2004,12 (4):1-5. [2] Patton A J. Modelling asymmetric exchange rate dependence[J].International Economic Review,2006,47(2):527-556. [3] 柏满迎,孙禄杰.三种Copula-VaR计算方法与传统VaR方法的比较[J].数量经济技术经济研究, 2007,(02):154-160. [4] 苟红军,陈迅,花拥军.基于GARCH-EVT-COPULA模型的外汇投资组合风险度量研究[J].管理工程学报,2015,9(1):83-193. [5] So M K P,Yeung C Y T. Vine-copula GARCH model with dynamic conditional dependence[J].Computational Statistics and Data Analysis,2014,76:655-671. [6] Reboredoa J C, Andrea U. Downside /upside price spillovers between precious metals: A vine copula approach[J].North American Journal of Economics and Finance,2015,34: 84-102. [7] 叶五一,李潇颖,缪柏其.基于藤Copula方法的持续期自相依结构估计及预测[J].中国管理科学,2015,23(11):29-38. [8] 杜子平,闫鹏,张勇.基于“藤”结构的高维动态copula的构建[J].数学的实践与认识,2009,39(10):96-102. [9] Sklar A. Fonctions de répartition àn dimentions et leursmarges[J].Publication de I’Institut de Statistique de L’Universit-é de Paris:1959,8: 229-231. [10] Aas K,Czado C,Frigessi A,et al. Pair-copula constructions of multiple dependence[J].Insurance:Mathematics & Economics, 2009,44(2): 182-198. [11] Kupiec P.Techniques for verifying the accuracy of risk measurement models[J]. Journal of Derivatives,1995,3:73-84. [12] Brock W, Dechert W, Scheinkman J.A test for independence based on the correlation dimension[R].Working Paper,University of Wisconsin at Madison, University of Houston,and University of Chicago,1987. [13] Mcneil A J,Frey R.Estimation of tail-related risk measures for heteroscedastic financial time series:An extreme value approach[J]. Journal of Empirical Finance,1998,7(3-4):271-300. [14] Pickands J. Statistical inference using extreme order statistics[J].The Ann als of Statistics, 1975,3(1):119-131. [15] 韦艳华,张世英.Copula理论及其在金融分析上的应用[M].北京:清华大学出版社,2008. [16] Hallerbach W G. Decomposing portfolio value at risk:A general analysis[J]. Journal of Risk,2003,5(2):1-18. [17] 杜红军,王宗军. 基于Copula-AL法的VaR和CVaR的度量与分配[J].中国管理科学,2012, 20(3):1-9. [18] 胡海鹏,方兆本.投资组合VaR及其分解[J]. 中国管理科学,2003,11(3):1-5. [19] 邵欣炜,张屹山. 基于VaR的证券投资组合风险评估及管理体系[J].数量经济技术经济研究,2003,12:66-70. Risk analysis of Foreign Exchange Portfolios Based on High-dimensional Dynamic Vine Copula HAN Chao, YAN Tai-hua (School of Economics and Business Administration, Chongqing University, Chongqing 400044, China) The structure of high-dimensional dynamic vine copula can overcome ‘dimensional curse’ faced by bivariate Copula and dynamically describe nonlinear dependence between multi-variables, and represents the academic frontier. Five kinds of foreign exchange log-returns, including USD, EUR, JPY, HKD and GBP, are selected to make empirical analysis, Time series are fitted with AR-GJR-GARCH and GPD models. After probability integral transform, high-dimensional dynamic C and D vine copulas are modelled. Then, portfolio VaR sets are got by Monte-Carlo method, tested by UC back testing, and compared to the corresponding static research. The results show that VaR based on high-dimensional dynamic C vine copula performs the best, and marginal risk of USD is considered as the least by VaR decomposition, the more USD the lest risk. The conclusions provide a new model and method to quantify risk, reasonably allocate asset portfolio, and for authorities to regulate risk. AR-GJR-GARCH model; high-dimensional dynamic vine copula; portfolio risk of foreign exchange; VaR; UC back testing 1003-207(2017)02-0010-11 10.16381/j.cnki.issn1003-207x.2017.02.002 2015-11-09; 2016-10-05 国家自然科学基金资助项目(71373296) 严太华(1964-),男(汉族),重庆璧山人,重庆大学经济管理学院,博士生导师,教授,研究方向:金融工程,E-mail:875071743@qq.com. F830.9 A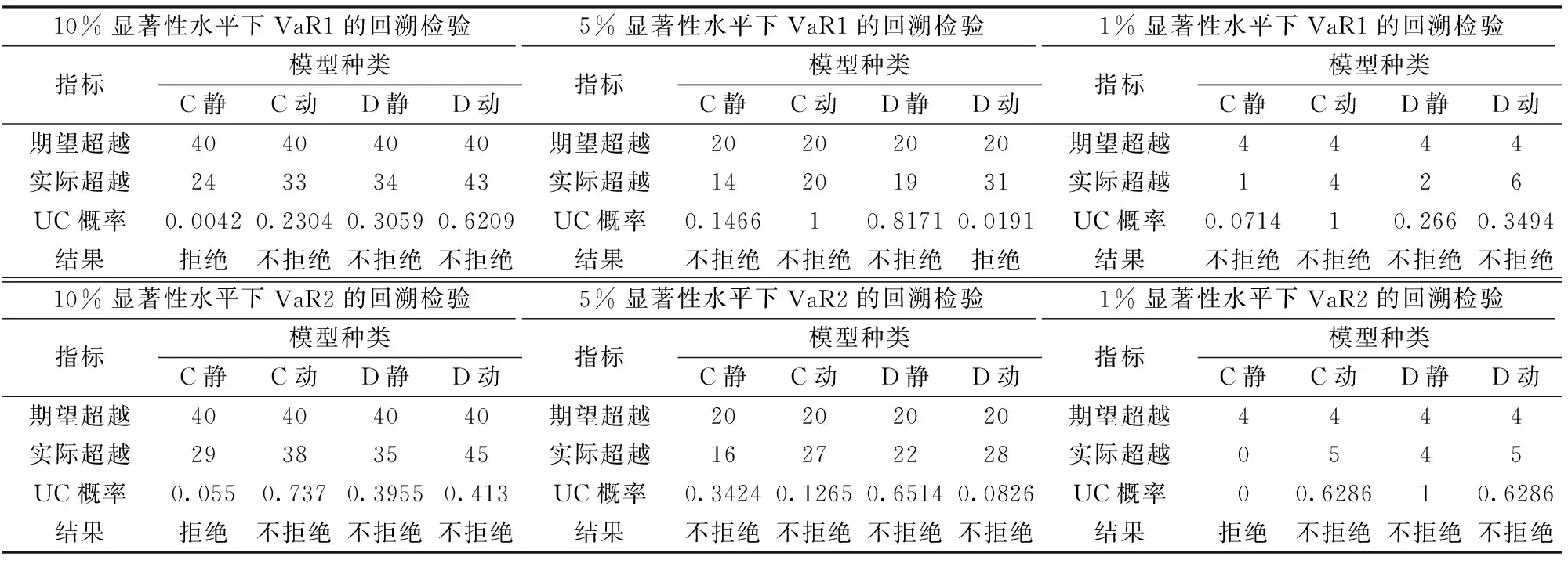
5 VaR的分解与最小VaR的资产权重

6 结语

