一道高考题引出圆锥曲线的一个性质

甘肃省兰州市第二十七中学 (730030) 陈鸿斌 张文奇

一道高考题引出圆锥曲线的一个性质

甘肃省兰州市第二十七中学 (730030) 陈鸿斌 张文奇

(Ⅰ)当t=4, |AM|=|AN|时,求ΔAMN的面积;

(Ⅱ)当2|AM|=|AN|时,求k的取值范围.

本题是2016年新课程高考数学理科试题全国卷Ⅱ第20题.本题的椭圆表达形式与2015年新课程高考数学理科试题全国卷Ⅱ第20题类似,都带有一个未知参数,但是形似神不同,富有创新性,内涵丰富,蕴含着椭圆的一个性质,无疑是一道经典之作.

笔者通过探究,得到了圆锥曲线又一个弦过定点的性质.

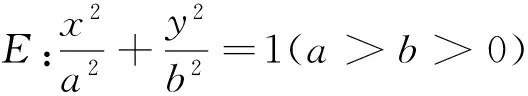
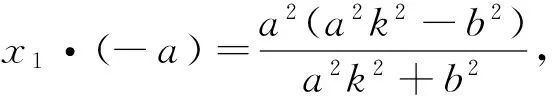
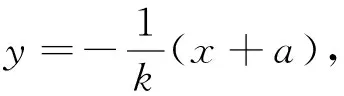
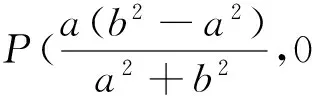
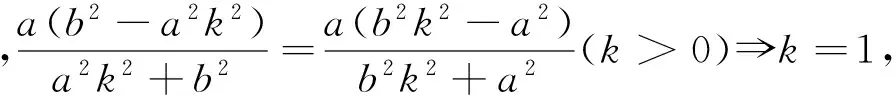
当l的斜率存在时,kPM=

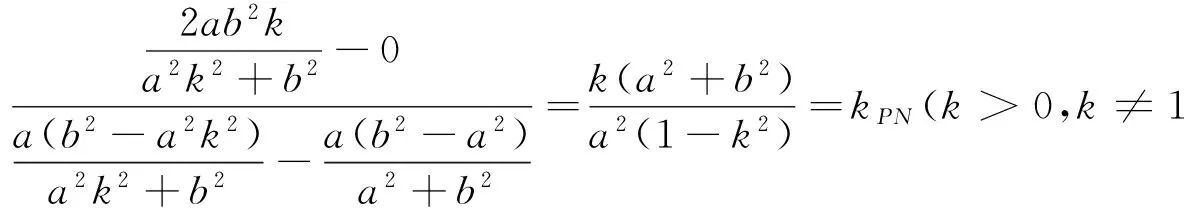
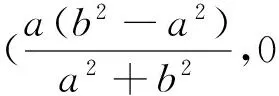
充分性:设M(x1,y1),N(x2,y2),不妨设点M的纵坐标y1>0.

所以ΔAMN是等腰直角三角形,故MA⊥NA.

=(1+k2)x1x2+(a-tk2)(x1+x2)+a2+k2t2

综上可知,MA⊥NA.

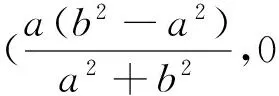
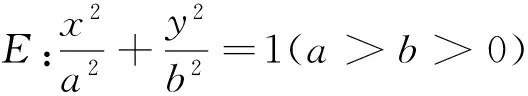
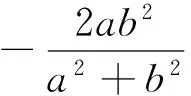
故ΔAMN是等腰直角三角形.

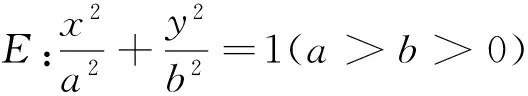
推论2由定理1可以直接得到,故从略.

笔者再次深入探究,将上述结论推广到双曲线和抛物线上,得到了下面的结论.

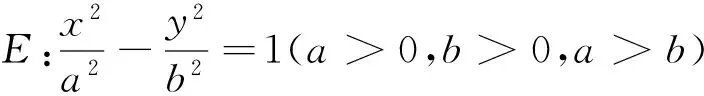
定理2的证明与定理1相同,故从略.

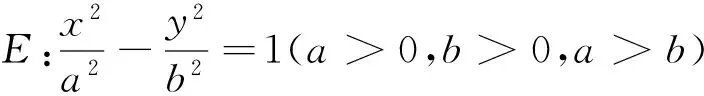
证明同于推论1,从略.

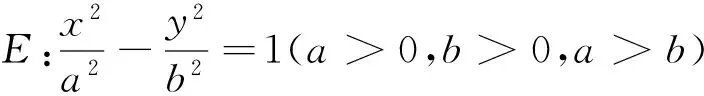
由定理2可以直接得出推论4.

定理3若直线l交抛物线E:y2=2px(p>0)于异于顶点O的两点M,N,则MO⊥NO的充要条件是l过定点(2p,0).

推论5 若过点(2p,0)并垂直于x轴的直线l交抛物线E:y2=2px(p>0)于M,N两点,则ΔOMN是等腰直角三角形.

推论6 若直线l交抛物线E:y2=2px(p>0)于异于顶点O的两点M,N,则以线段MN为直径的圆过O点的充要条件是l过定点(2p,0).

证明:同上,略.

一道经典的高考题蕴含着极其丰富的研究价值,我们应该用研究的态度看待每一道高考题,挖掘出一些丰富的内涵,有助于我们正确把握高考的命题趋势,为今后的教学工作做出有效的指导.