基本学情,积极引导
——例谈“多边形内角和”的教学
☉山东滨州市滨城区第六中学 王桂滨
基本学情,积极引导
——例谈“多边形内角和”的教学
☉山东滨州市滨城区第六中学 王桂滨
一、引言
目前,我国有关数学活动经验的理论研究与教学实践都比较薄弱,数学活动经验的内涵一直难以界定,至今尚未对数学活动经验的含义达成共识.多年来,一些专家学者撰文发表自己的看法,探究数学活动经验的确切含义,主要观点有以下几种:
1.数学活动经验是数学知识的一部分.“数学活动经验属于学生的主观性数学知识的范畴”,数学知识不仅包括数学事实,也包括数学活动经验.
2.数学活动经验是一种认识,特别是感性认识.个体的数学活动经验是对自己以往经历的数学活动在认知方面的自觉或不自觉的感性概括,是一种感性认识.也有的认为,数学活动经验是在数学目标指引下,通过对具体事物进行实际操作、考察和思考,从感性向理性飞跃时所形成的认识.
3.数学活动经验是体验,是经历.数学活动经验是学生经历数学活动之后所留下的直接感受、体验和感悟.这些具有个体特色的内容,既可以是感觉知觉的,也可以是经过反省之后形成的经验.
4.数学活动经验既是知识,也是过程.数学活动经验分为静态和动态两个层面.数学活动经验介于缄默知识和显性知识之间,从静态上看是知识,是学生对整个数学活动过程产生的认识,包括体验和感悟等;从动态上看是过程,是经历.
5.数学活动经验是组合体的整体概念.数学活动经验是指学习者在参与数学活动的过程中所形成的感性知识、情绪体验和应用意识.感性知识是指具有学生个人意义的过程性知识;情绪体验是指对数学的好奇心和求知欲、在数学学习活动中获得的成功体验、对数学严谨性与数学结果确定性的感受,以及对数学美的感受与欣赏等;应用意识包括“数学有用”的信念、应用数学知识的信心、从数学的角度提出问题与思考问题的意识,以及拓展数学知识应用领域的创新意识.也有的认为,数学活动经验是学生从经历的数学活动过程中获得的感受、体验、领悟,以及由此获得的数学知识、技能、情感与观念等内容组成的有机组合性经验.
二、问题的提出
我国于2011年修订的《义务教育数学课程标准》在课程目标中明确提出“四基”,即使学生“获得适应社会生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本经验活动”.在传统的“双基”基础上增加了数学的基本思想和基本活动经验.现以人教版义务教育教科书数学八年级上册第11章第三节“多边形的内角和”教学为例,谈一谈具体的做法和实践心得.
三、“多边形内角和”内容解析
1.地位及作用.
2011年修订的《义务教育数学课程标准》对多边形内角和的教学要求是“探索并掌握多边形内角与外角和公式”,从课标可以看出,对于多边形的内角和和外角和强调了知识的发展过程,这就要求教师在教学时应创造有利于学生探索的教学情境.
2.多边形内角和与外角和的教学分析.
本节课是人教版义务教育教材数学八年级上册第11章11.3.2第一课时,是在探究了三角形的内角和与外角和,并学习了多边形的有关概念的基础上进行的,学生已初步具备对数学问题进行论证的逻辑推理能力,这节课需要学生在已有的知识、生活经验的基础上来学习.
四、学习过程
1.问题情景.
(1)三角形的内角和是多少?
设计说明:本节课对于多边形的内角和,主要是借助三角形的内角和求解.
(2)三角形的内角和定理是如何证明的?
设计说明:多边形的内角和定理与三角形内角和定理的证明思想方法是一致的.
生1:如图1,过顶点A作EF∥BC.
因为EF∥BC,所以∠FAC=∠C,∠EAB=∠B.
因为∠FAC+∠EAB+∠BAC=180°,所以∠C+∠B+∠BAC=180°.
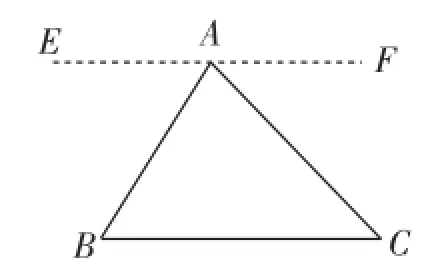
图1
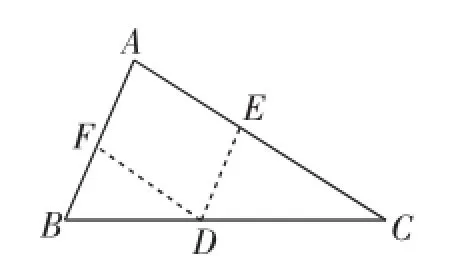
图2
生2:如图2,在边BC上任取一点D(异于B、C),作DE∥AB,DF∥AC.
因为DE∥AB,DF∥AC,所以∠B=∠EDC,∠C=∠FCB,∠A=∠DEC,∠FDE=∠DEC.
又因为∠FDE+∠EDC+∠FDB=180°,所以∠A+∠B+∠C=180°.
生3:如图3,在△ABC内部任取一点D,过点D作MN∥AB,EF∥AC,HG∥BC.
因为MN∥AB,HG∥BC,所以∠B=∠MNC=∠MDG.同理∠A=∠DFH=∠FDM,∠C=∠FEB=∠FDH.
而∠FDM+∠MDG+∠FDH=180°,所以∠A+∠B+∠C=180°.
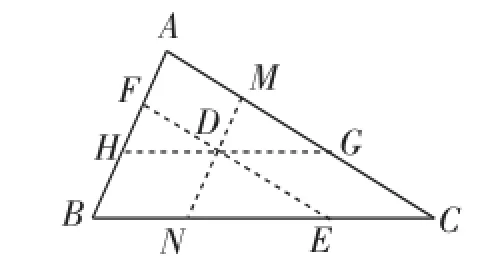
图3
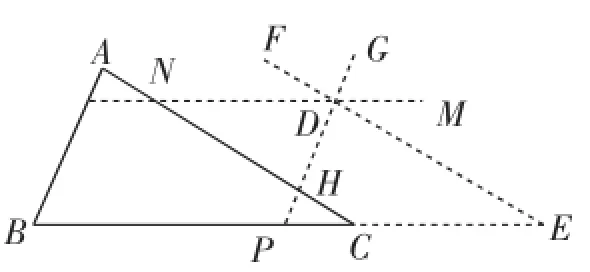
图4
生4:如图4,在△ABC外部任取一点D,过点D作MN∥BC,EF∥AC,HG∥AB.
因为EF∥AC,HG∥AB,所以∠A=∠CHP=∠EDH.
同理∠B=∠HPC=∠HDN,∠ACB=∠E=∠FDN.
而∠EDH+∠HDN+∠FDN=180°,所以∠A+∠B+∠ACB=180°.
师:通过以上四位同学的回答,我们可以总结:分别过三角形的顶点、边、内部和外部作平行线,构造平角,证明了三角形的内角和定理.
设计说明:四位学生的回答回顾了以前学习三角形内角和定理的证明方法,为本节课多边形内角和定理的证明作铺垫,也就是积累了解决多边形相关问题的活动经验.
2.多边形的内角和.
(1)我们小学学过哪些多边形?它们的内角和是多少?
生1:学过正方形、长方形,因为它们的每一个内角均为90°,所以它们的内角和均为360°.
(2)是否所有的四边形的内角和均为360°?
设计说明:因为小学学过的长方形、正方形的内角和为360°,猜想一般四边形内角和的度数,向学生渗透由具体到抽象、由特殊到一般的数学思想方法.
师:怎么将这个问题转化为我们已知的问题呢?
生:可以转化为三角形的问题.
师:如何转化呢?
生1:可以连接四边形的对角线,例如,如图5,在四边形ABCD中,连接AC.
将四边形分割为两个三角形.因为每个三角形的内角和为180°,所以四边形的内角和为360°.

图5

图6
生2:如图6,还可以在四边形内部取一点E,然后连接EA、EB、EC、ED.
四边形被分解为四个三角形,这四个三角形每个的内角和为180°,总的内角和为720°,又因为中间多了一个周角,所以四边形的内角和是360°.
生3:如图7,还可以在边BC任取一点E,然后连接EA、ED.
四边形被分解为三个三角形,这三个三角形每个的内角和为180°,总的内角和为540°,又边BC上多了一个平角,所以四边形的内角和是360°.

图7
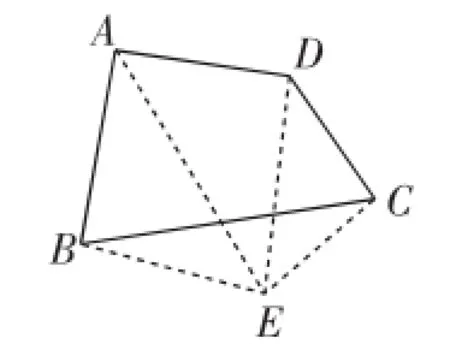
图8
生4:如图8,还可以在四边形的外部任取一点,连接EA、EB、EC、ED.
四边形的内角和等于△ABE、△ADE、△DCE的内角和再减去△BCE的内角和,所以四边形的内角和为360°.
师:四位同学的回答很精彩,我们可以发现四位同学的思路与前面证明三角形内角和的思维方法是一致的,同学们,我们在以后的学习过程中,要学会将未知问题转化为已知问题.
师:请同学们选择自己喜欢的方法来探索五边形、六边形、七边形的内角和,并将探索的结果填入表1.

表1
(学生通过实验、探究顺利完成了表1)
3.多边形的外角和.
(1)正方形、长方形的外角和是多少度?
设计说明:对于长方形、正方形,学生能够很快算出它们的外角和,从而向学生渗透从特殊到一般的数学思想.
师:是否任意一个四边形的外角和都是360°?
(学生思考)
生1:如图9,∠NAB+∠BAD=180°,∠EBC+∠ABC= 180°,∠DCF+∠BCD=180°,∠ADC+∠ADM=180°,四边形的内角和为∠ABC+∠BCD+∠CDA+∠DAB=360°,所以四边形的外角和为360°.

图9

图10
生2:如图10,过点C作CH∥AD交AB于H点,CE∥AB.
显然可以得到∠NAB=∠AHC=∠HCE,∠HBC=∠ECF,∠ADM=∠HCD.
而∠DCH+∠HCE+∠ECF+∠DCF=360°,所以四边形的外角和为360°.
生3:如图11,过点P作PO∥AB,PH∥CD,PM∥AD.
容易得到∠QAB=∠AEP=∠EPI,∠CBE=∠CPI,∠DCF=∠HPC,∠NDA=∠AHZ=∠EPH.
同生2,可以得到四边形的外角和为360°.
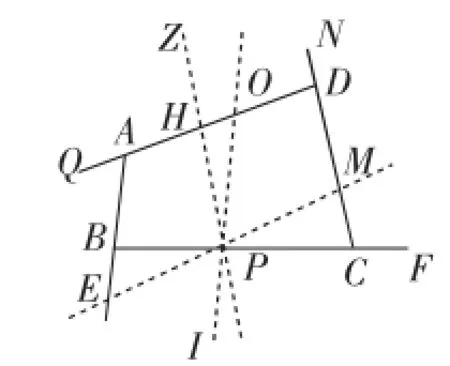
图11

图12
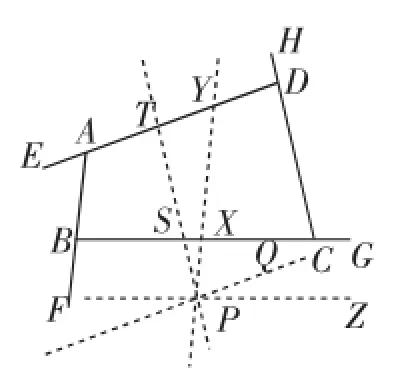
图13
生4:如图12,也可以在四边形内部任取一点P,作XY∥AD,EF∥BC,KL∥CD,GH∥AB.
同样可以得出四边形的外角和为360°.
生5:如图13,也可以在四边形外部任取一点P,作XY∥AB,PQ∥AD,ST∥CD.
同样可以得出四边形的外角和为360°.
师:以上五位同学的回答实在是太精彩了,五位同学从不同的思路出发,得到了相同的结果,真可谓“条条大路通罗马”.
师:请同学们选择自己喜欢的方法来探索五边形、六边形、七边形的外角和,并将探索的结果填入表2.

表2
(学生通过实验、探究顺利完成了表2)
以上各类证明方法充分彰显出学生个性化的思维,以及学生综合运用基础知识、基本技能的能力,即立足于一般的解法,又基于学生的数学基本活动经验.
五、教学导向
1.深挖教材.
学生的学习是人类发现基础上的再发现过程.教材是经过教学法加工了的素材,加之教学进度的要求,或多或少会影响学生数学活动经验的积累.经过反复审查形成的教学素材,形成了教学的基本概念、基本理论.因此教师在平时教学时,要充分利用教学素材,挖掘教材;知识的挖掘往往是一个永无止境的过程,学生学习数学的能力是有差异的,因此我们在挖掘教材时,要着重考虑课标要求,进行科学、合理、有发散的变式,避免通过“题海战术”增加学生负担.当前的许多中考试题,往往都源于教材,因此我们应该深挖教材,利用好教材.
2.关注数学活动经验的获得.
过去数学强调的是双基“基础知识和基本技能”.从1953年提出,到1956年写出之后,一直成为中国数学教育的核心.基础知识和基本技能功不可没,使得中国数学基础教育在世界上影响很大,许多数学课堂讲的基本上是逻辑,是论证,是定理的证明过程,而不是发明定理的过程,也不是发现定理证法的过程.这对培养学生的创造力是十分不利的.我们最新的课程标准加了两个,一个是基本思想,另一个是基本活动经验,成为“四基”,帮助学生进行思考经验的积累,问题提出的经验的积累,创新性活动的积累.因此在平时的教学中,一方面要关注数学知识、技能、思想方法的学习,另一方面要通过数学活动经验启智学生,让学生正真参与到数学的学习之中,享受数学.
1.黄翔,童莉.获得数学活动经验应成为数学课堂教学关注的目标[J].课程·教材·教法,2008(1).
2.马复.论数学活动经验[J].数学教育学报,1996(11).
3.张奠宙,竺仕芬,林永.“数学基本活动经验”的界定与分类[J].数学通报,2008(5).
4.孔凡哲.基本活动经验的含义、成分与课程教学价值[J].课程·教材·教法,2009(3).
5.单肖天,景敏.数学活动经验及其对教学的影响[J].课程·教材·教法,2008(5).
6.王新民,王富英,王亚雄.数学“四基”中“基本活动经验”的认识与思考[J].数学教育学报,2008(3).
7.仲秀英.学生数学活动经验的内涵探究[J].课程·教材·教法,2010(10).
8.史宁中,柳海民.素质教育的根本目的与实施路径[J].教育研究,2007(8).
9.史宁中.数学思想概论·图形与图形关系的抽象[M].长春:东北师范大学出版社,2009.

