初中“选学内容”的教学实践与思考
——以“三元一次方程组习题课”为例
☉江苏南通市通州区刘桥中学 钱海燕
初中“选学内容”的教学实践与思考
——以“三元一次方程组习题课”为例
☉江苏南通市通州区刘桥中学 钱海燕
我们知道,《义务教育数学课程标准(2011年版)》把解三元一次方程组放在选学内容,这样各级教材就给相关内容打上了“选学”的印记,并规定选学内容不得出现在中考范围.然而我们也知道,无论是七年级二元一次方程组含参数的问题,还是九年级二次函数的解析式的确定,如果学生能熟练解三元一次方程组,则可为上述问题提供丰富的解决方法,所以,我们认为在七年级下学期教学三元一次方程组时,为了促进学生深刻理解学段前后知识,仍然应该对学生提出学会解三元一次方程组的要求,特别是对具有特殊系数特点的应该专题训练.本文给出一个关于快速求解特殊三元一次方程组的教学案例,并跟进阐释相关教学理解,供研讨.
一、特殊三元一次方程组解法的教学设计
(一)对教学内容的认识:解三元一次方程组是在学习了二元一次方程组解法的基础上进一步体会“消元”的思想方法,通过“消元”把三元一次方程组转化为二元一次方程组,进而转化为一元一次方程.对于某些特殊形式的三元一次方程组,可以根据方程组的特征采取特殊的方法求解,这样做既能提高解题速度,还能体会一些数学思想方法,感受数的魅力.
(二)教学流程.【例题选讲】
例1解三元一次方程组:
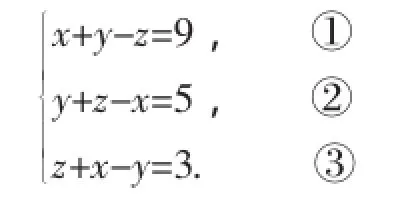
分析:当方程组中的方程形式特殊时,除了常用的代入消元法和加减消元法外,还可以根据题目的特点,用特殊的方法来求解.根据三个方程中系数的特点,可以采用整体加减法来求解.
预设PPT讲解(如图1):

图1
反思:此题主要考查三元一次方程组中各未知数的系数具有某种特殊规律时,这样的方程组可以采用整体加减法来求解,以达到快速求解的效果.
例2解三元一次方程组:

分析:对于这个方程组,如果用常规方法消元比较烦琐,观察方程的特点,不难发现方程①中的4x-12y= 4(x-3y),这样就与方程②有了联系.把方程②整体代入方程①就可以求出z的值,从而快速将这个三元一次方程组转化为二元一次方程组,达到消元求解的目的.
预设PPT讲评(如图2):

图2
反思:此题主要考查三元一次方程组中的一个方程(或经过变形整理后的方程)中出现整体代数式时,可以采用整体代入的方法消元求解.
例3解三元一次方程组:

(2)可以由①和②求得x:y:z的值,再求解.
预设PPT讲评(如图3和图4):

图3

图4
反思:此题主要考查三元一次方程组中出现未知数的比例式时,可用设比值参数法消元求解.这里的k被称为辅助未知数(或参数).第(2)问的难点在于沟通三个未知数之间的比例关系.
【巩固练习】

2.若x+3y-2z=-6,4x+2y+7z=21,则x+y+z的值为____.
4.解三元一次方程组:

二、教学设计立意解读
1.“教什么”,习题课重在选题,贴近教材,变式生长.
习题课教学不像新授课,教材上有概念呈现、例题配备.对于习题课教学来说,首先面临的是教学内容的选取、组织,贴近教材、变式拓展的选题十分重要.本课所选例、习题有不少就是改编自教材上的习题,还有一些精选自相关教辅资料,围绕特殊系数三元一次方程组来选题,为的是让学生在学习过程中善于观察方程组中未知数系数的特点,再灵活选择消元策略.
2.“怎么教”,精心设计讲评课件,渐次呈现,展示思路.
在选题之后,需要精心设计讲评方式,上文中我们对例题思路讲评的PPT进行了设计,利用PPT动画渐次呈现的方式把方程组消元的思路富有启发式地展示出来,让学生在这样的讲评过程中懂得观察系数的特点,感悟思路贯通的方式,提高解特殊形式三元一次方程组的技能.
3.“教谁”,认真研判所教学生的学情水平、未来发展可能.
教学经典问题最重要的就是学情研判,针对所教学生开展教学是教学预设最需要重视的.因为如果学生对二元一次方程组消元的策略还不能很好地掌握,那三元方程组的消元也将会是一个难以实现的教学目标.除此以外,还需要考虑所教学生在未来学习二次函数解析式的确定时,是否需要灵活运用三元一次方程组的解法技能.因为根据教学经验,到了九年级,仍然有少数学生对三元一次方程组的解法还比较陌生,那他们学习经过三个点确定抛物线的解析式时,也就更显困难重重了.
三、对选学内容的初步思考
1.选学内容要因地制宜、因生而异.
正是因为我国地广人多,各地教育发展难以整齐划一,加上学生个体差异也客观存在,所以《义务教育数学课程标准(2011年版)》设计不少选学内容是十分有必要的.这就要求在日常教学中,我们要根据本校实际、本班实际、学生实际,提供选学内容的相关教学,让不同学生在数学上都能得到不同发展,这也是教育公开的内涵之一.有专家提出“课程标准是底线要求,但不是天花板”的说法是有道理的.
2.选学内容要考虑部分学生高中阶段学习的需求.
就我们跟高中教师的调研和研讨所见,目前初中阶段因为不少选学内容的教学不到位,使得初中群体占一半左右的学生进入高中之后不能很快进入高中阶段的学习,不少高中还需要开设初、高中衔接的教学,不少教辅资料专题定位在初、高中衔接的方法,而这类资料培训的重点往往是扩充数式运算中的二次根式的化简(繁杂根式的分母有理化)、乘法公式、因式分解(特别是十字相乘法、分组分解法)、二元二次方程组、一元二次方程中根与系数关系的灵活运用;函数中特别是直线与抛物线相交、基于对称考虑二次函数的图像等内容;几何领域的相似三角形、圆中也有不少定理或性质需要补充.基于上述认识,我们认为,初中阶段在习题课教学或数学活动课中,所选的拓展内容上,可以在相关专题上适当拓展,为一些高层次学生打开一扇窗.
1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
2.郑毓信.数学教师如何才能用好教材[J].小学教学(数学版),2016(3).
3.王友峰.专业自主增设内容,回看陈题洞察结构——九年级“探究四点共圆”教学设计与解读[J].中学数学(下),2016(12).
4.陈爱军.预设互动促进对话,课件简约渐次展现——李庾南老师“函数的图像”课例赏析[J].中学数学(下),2016(10).

