基于关联视角,实践“用教材教”
——以“从二次函数视角看一元二次方程”教学为例
☉江苏南通市易家桥中学 徐向清
基于关联视角,实践“用教材教”
——以“从二次函数视角看一元二次方程”教学为例
☉江苏南通市易家桥中学 徐向清
最近一次教研活动中,笔者有幸执教“从二次函数视角看一元二次方程”研讨课,该课没有简单照搬教材内容,而是从学生已有经验出发,先复习一次函数与一元一次方程之间的关系,然后引出二次函数与一元二次方程之间的关系,取得较好的教学效果.本文先整理该课的教学流程,并阐释教学立意,供分享.
一、“从二次函数视角看一元二次方程”教学流程
教学环节(一)热身练习,回顾旧知.
(1)一次函数y=2x-6中,当y=0时,求自变量x.
(2)一次函数y=2x-6中,当y=2时,求自变量x.
(3)当一次函数y=2x-6与y=-x+3的函数值相等时,求自变量x.
设计意图:讲评时注意让学生展示一元一次方程的解,对应着直线(一次函数的图像)与x轴的交点坐标之间的关系,具体如下:
(1)一次函数y=2x-6中,当y=0时,可得方程2x-6=0,解得x=3.即一次函数值为0时,自变量x=3,此时也可得直线y=2x-6与x轴的交点的横坐标为3.
(2)一次函数y=2x-6中,当y=2时,可得方程2x-6=2,解得x=4.即一次函数值为2时,自变量x=4,此时也可得直线y=2x+6与直线y=2的交点的横坐标为4.
(3)当一次函数y=2x-6与y=-x+3的函数值相等时,可得方程2x-6=-x+3,解得x=3.此时也可得直线y=2x-6与直线y=-x+3的交点的横坐标为3.
预设PPT渐次呈现如下的对应关系图(如图1):

图1
教学环节(二)两道问题,探究新知.
问题1:以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t-5t2.
(1)小球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(2)小球的飞行高度能否达到20m?如果能,需要多少飞行时间?
(3)小球的飞行高度能否达到20.5m?为什么?
(4)小球从飞出到落地要用多少时间?
思路简述:将h的值代入二次函数的解析式可以得到关于t的一元二次方程,则根据方程是否有符合实际的解来说明小球的飞行高度能否达到所给的值.
预设讲评PPT截图如同2所示:

图2
预设点评:通过上述问题的解决,大家从“数”的角度认识到二次函数与一元二次方程的关系:“已知二次函数y=ax2+bx+c的值为0,求自变量x的值”即为“求解一元二次方程ax2+bx+c=0”;反之亦如此.
问题2:下列二次函数的图像与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数值是多少?你能得出相应的一元二次方程的根吗?二次函数的图像与一元二次方程具有怎样的联系?
(1)y=x2+x-2;(2)y=x2-6x+9;(3)y=x2-x+1.
思路简述:x轴上的点的纵坐标均为0,即二次函数的函数值为0,所以可将y=0分别代入二次函数的解析式,可得相应的一元二次方程,根据一元二次方程根的情况即可判定抛物线与x轴的交点的情况.
预设讲评PPT(如图3):
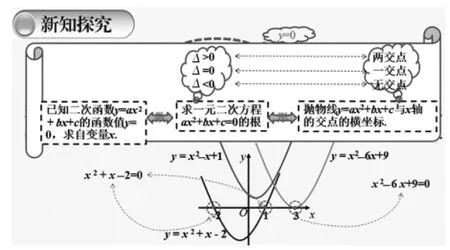
图3
预设点评:通过上述问题的解决,可以发现二次函数的图像与一元二次方程也有关系:(1)抛物线与x轴的交点个数与相应一元二次方程根的情况相关;(2)抛物线与x轴的交点的横坐标即为相应一元二次方程的两根.
教学环节(三)练习训练,巩固新知.(略)
教学环节(四)课堂小结,梳理归纳.
通过前面的学习,大家可以发现“求一元二次方程ax2+bx+c=0的根”,从数的角度可看作“已知二次函数y= ax2+bx+c的函数值y=0,求自变量x”;从形的角度看“一元二次方程ax2+bx+c=0的根的情况”与“抛物线y=ax2+bx+c与x轴的交点的个数”相关,且“方程ax2+bx+c=0的根”为“抛物线y=ax2+bx+c与x轴的交点的横坐标”.一边讲解,一边动画呈现如下PPT(如图4):

图4
拓展思考:有了前面的学习经历,可以变式思考如下一些问题:
例如:方程x2-2x+3=6的根,从数的角度可看作二次函数y=x2-2x+3的函数值y=6时对应自变量的值,从形的角度可看作抛物线y=x2-2x+3与直线y=6的交点的横坐标.同时,结合图像可以发现抛物线y=x2-2x+3与直线y=2有1个交点,说明方程x2-2x+3=2有2个相等的实数根;抛物线y=x2-2x+3与直线y=1没有交点,说明方程x2-2x+3=1无实数根.因此“一元二次方程ax2+bx+c=h的根的情况”与“抛物线y=ax2+bx+c与直线y=h的交点个数”相关.
二、教学立意的进一步阐释
1.理解数学,在数学内在联系处创设情境、引入新课.
初中数学富含联系,特别是数式、方程与函数的知识都可统一在函数的高观点之下,这在八年级学习一次函数之后就能感受出来.学生从一次函数的视角再认识了此前所学的一元一次方程、二元一次方程组、一元一次不等式(组)等知识,“站在高处”俯看旧知别有一番认识在心里.本课没有沿用教材上的情境引入,而是用所谓“复习旧知”的方式引入新课,但这种复习旧知又不是简单的知识再现,而是对比了从一次函数视角看一元一次方程,本课所学习的是从二次函数视角看一元二次方程,这样它们之间的一致性就得到了显现.
2.设计课件,让讲解、点拨与小结在渐次呈现中助学.
最近《中学数学》(下)不少课例文章中附了课件PPT截图,对于课堂教学设计中的课件制作提出了有益参考,特别是相关课例中的课件使用了渐次呈现、标注提示等方式,使得课件的功用得到发挥,过渡了不同教学环节,突出了教学重点,化解了教学难点,使得学生的注意力得到提升.这就是我们在上文中也附出几幅PPT截图的原因,目的是让更多的同行能感受到不同教学重点或难点突破的多样化努力.
3.拓展思考,课堂小结时为学生打开窗户、向上挑战.
由于教学时间所限,我们在课堂小结之后给学生拓展视角,把一元二次方程一般式的形式推广到了方程等号右边不是0的情形,对应着二次函数图像与直线y=h相交的情形.这种拓展思考有一定的挑战,但是对优秀学生来说是可以接受的,因为在八年级学习一次函数时,就曾研究过类似直线y=x+1与直线y=2的交点问题(对应着方程x+1=2).这里值得一说的是,关于教学深度的话题,即使是新授课,也可以在小结阶段结合本课的内容帮助一些优秀学生走向纵深方向,就如同为学生打开一扇窗一样,而不是“封闭着”,我们需要的是给优秀学生提供深入思考的机会.
三、写在最后
郑毓信教授关于数学教师如何才能用好教材提出他的一些深刻见解,归根结底是需要我们保持独立思考、深入思考,基于理解数学的高度,抛却“纲本主义”,基于自己修炼的“善于举例、善于提问、善于优化”的基本功,认真组织教学内容、规划教学进程、预设教学课件等,追求更有数学味、更加开放的数学课堂.想来,本文中的课例只是围绕上述高要求的一次课例实践,做得还不到位,我们还有很长的路要走.
1.章建跃.构建逻辑连贯的学习过程使学生学会思考[J].数学通报,2013,56(6).
2.刘东升.我们需要怎样的“问题”驱动课堂——由美国莎维女士执教的函数图像课说起[J].教育研究与评论(课堂观察版),2016(11).
3.郑毓信.“开放的数学教学”新探[J].中学数学月刊,2007(7).
4.郑毓信.数学教师如何才能用好教材[J].小学教学(数学版),2016(3).

