返璞归真，让几何起始教学更有数学味——“直线、射线与线段”同课异构赏析

☉江苏海安县曲塘中学附属初级中学戴路

返璞归真，让几何起始教学更有数学味
——“直线、射线与线段”同课异构赏析

☉江苏海安县曲塘中学附属初级中学戴路

现如今，自媒体时代拉近了我们与教研现场的距离，拓展了教研活动的传播范围，比如，近期我们在网络上关注到在南通市初中数学学科基地活动上，开展了多个课题的同课异构活动，笔者认真研习了两节“直线、射线与线段”（第1课时），为两位开课老师对初中几何起始教学的深刻理解而赞叹，也为该地区教研活动的返璞归真、不求热闹的情境设置而感慨.本文概述两节课的教学流程，并针对这两节课给出一些评课与赏析，供研讨.

一、同课异构“学生活动单”

“学生活动单”（一）

学习目标：

1.掌握“两点确定一条直线”的基本事实；

2.进一步认识直线、射线、线段，掌握直线、射线、线段的表示方法；

3.初步体会几何语言的应用.

学习活动：

活动一：说说图1中的点和直线的位置关系.

图1

活动二：按下列语句画图：（独立完成后小组交流）

（1）直线EF经过点C；（2）点A在直线l外；（3）射线OA与线段BC相交于点D；（4）直线AB与直线CD相交于点B.

检测反馈：

1.（10分）如图2，射线OA上有一点B，下列与射线OA是同一条射线的是（）.

图2

图3

2.（10分）如图3，下列说法错误的是（）.

A.点A在直线a上B.点A在直线b上

C.点B在直线a上D.直线a不经过B点

3.（30分）如图4，平面上有四个点A、B、C、D，根据下列语句画图：

（1）画直线AB、CD交于E点；

（2）画线段AC、BD交于点F；

（3）作射线BC.

图4

“学生活动单”（二）

学习目标：

1.掌握基本事实“两点确定一条直线”；

2.进一步认识直线、射线、线段，掌握它们的表示方法；

3.初步体会三种几何语言及它们的转化.

学习活动：

活动一：认识基本事实.（先自己尝试，后小组交流）如图5，经过点A和点B画一条直线，然后思考能画几条.

结论：经过两点有条直线并且直线.

图5

活动二：图形表示方法.

1.类比直线的表示法，表示图中的射线和线段.（先独立思考，后小组交流）

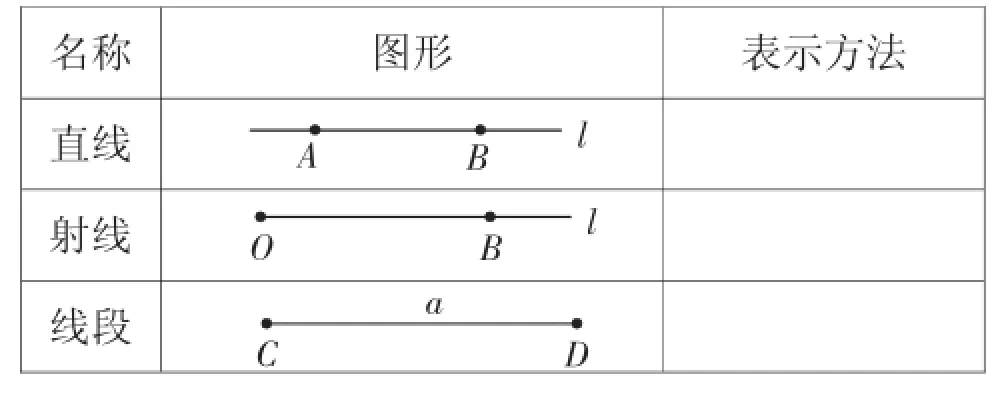
名称图形表示方法直线射线线段AB l O B l a C D

活动三：学习几何图形.

1.识图.

（1）用适当的语句描述下列图形（图6、图7）中点与直线（或直线与点）的关系.

图6

图7

（2）用适当的语句描述图8中点与直线的关系.

2.画图.

按下列语句画出图形：

（1）点P在直线AB上；（2）直线l不经过点A；（3）直线a、b、c都经过点O；（4）线段AB与直线CD相交于点B.

图8

检测反馈：

1.要钉一根水平方向的木条，至少需要_____个钉子，其理论依据为________.

2.如图9，下列说法错误的是（）.

A.点A在直线a上

B.点A在直线b上

C.点B在直线a上

D.直线a不经过B点

3.根据下列语句画出图形：

（1）A、B、C三点在直线m上，且点C在点A与点B之间；

（2）直线a与线段b相交于点O.

图9

二、课例赏析

1.辨别学段特征，返璞归真开展几何入门教学.

《义务教育数学课程标准（2011年版）》上关于课程目标是分不同学段详细要求的，然而我们注意到不少公开课、研讨课，或一些练习册上的习题选择往往对学段辨析不清，把小学阶段对直线、射线、线段的一些情境要求、教学要求拉到初中几何起始阶段继续训练，作为必要的复习还好，就怕有些课例为了增加所谓的教学趣味，把教学重点和用力点都消耗在这些情境内容上.而我们看到的这两节同课异构课例，教师及背后打磨团队显然对学段的辨析是十分到位的，没有重复小学学段对直线、射线和线段的要求，而是直接进入初中几何对相关概念的教学，返璞归真，不玩花架子，直截了当，把一节课上得很有数学味道，值得学习.

2.追求简约教学，让繁冗的导学案走向简约.

就我们在一些网站或“超级学校”（平行班级数在15个班以上）的观摩学习所见，当前导学案的使用在数学教学中十分流行，在所谓集体备课的要求下，教案打磨成了选题充实到导学案上去，而这些导学案多沦落为“习题单”，抛开教材搞教材的现象不在少数.就这些导学案来说，小题数的繁多，栏目之间的繁杂也是导学案的大问题.我们见到的上面两课例的学生活动单却是另外的面貌，活动简约，大量留白，教师针对两三个活动跟学生展开充分的对话、生成新知，使得教学环节走向简约，对话追求深度.这样的导学单值得导学案研究者们关注.

3.重视课堂反馈，改编习题有效检测学习效果.

在这两节课的教学环节中，两位教师都留出10分钟左右用于当堂检测，看似是应试教学的教学行为，其实细细考察两位老师所选的教学检测题，足见功夫，比如，题型多样，有选择、填空、解答，设计分值让学生有紧张感，由易到难，题干、设问简明，指令清晰，学生只要在该课上认真学习，就能完成得很好.以第2小题为例，注意反向设问，训练学生纠错、质疑、批判思维.

三、写在最后

观摩研习两节课例时，恰关注到我国著名数学教育家单墫对初中几何教学的一些评论，比如，单教授认为，数学是门严谨的学问，尤其平面几何，是有一个体系的，前几个知识点告诉你“是什么”，下面就要告诉你“为什么”.现在你只讲“是什么”，“为什么”要到一年以后再讲，这个体系就切断了，思维探究的精神就弱了.想来，如果初中几何起始阶段只是停留在小学学段的情境化、幼稚化的训练上，忽略几何定义的精确，图形语言、符号语言的训练，则后续学习推理时学生往往难以适应，造成几何学习方面的困难.笔者与备课组内其他同行交流时还有一个观点，南通市启秀中学李庾南老师从教六十年，至今仍然坚守在课堂一线，李老师对该地区的初中教学的影响是全面而深刻的（当然，就我们在《中学数学》（下）上见到的很多李老师的课例来说，李老师的影响已不只在南通地区了），我们从上面这两节课的返璞归真，不也能看出一些端倪吗？

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.

2.马公仕.靠近“最近发展区”，聚焦初中几何特点——以七年级“直线、射线、线段”教学为例［J］.中学数学（下），2015（3）.

3.鲍建生，顾冷沅等.变式教学研究［J］.数学教学，2003（1、2、3）.

4.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013，56（6）.

5.章建跃.创新推动改革，全面提高教育质量——暨“第九届初中青年数学教师优秀课展示与培训活动”总结［J］.中国数学教育（初中），2016（4）.