数学定理教学方法——以“相似三角形判定定理1”为例

☉浙江象山县石浦中学邬云德

数学定理教学方法
——以“相似三角形判定定理1”为例

☉浙江象山县石浦中学邬云德

一、背景介绍

定理是用推理的方法判断为正确的命题，它包括数学中的性质定理、判定定理、公式等.定理与原理“一字之差”，但逻辑形式却有天壤之别.原理教学主要是由特殊到一般的归纳推理，定理教学主要是由一般到特殊的演绎推理；原理主要接受实践的检验，定理必须经过逻辑的证明；原理教学可以借用“概念形成”的方式来进行，定理教学要经历“提出问题→操作观察→归纳猜想→分析证明→多样表达→解决问题→反思内化”的过程.但在以浙教版数学九年级上册第四章第4节“相似三角形的判定定理1”为载体的“多人同课异构”式的研修活动中发现，课堂教学普遍没有遵循定理教学的基本规范.网上查阅同类课例发现也有类似现象.鉴于此，笔者在重复式观课与反思的基础上，对该课的教学进行重建，改进后的教学过程与效果得到了同仁的认可.现将其整理出来，以飨读者.

二、教学实录

环节1：经历回顾并提出问题的过程——明确研究问题.

师：我们在研究两个三角形全等的判定时，用分类探索的策略和用画图与实验来证实（或用推理方法来证明）的方法，获得了判定两个三角形全等除定义外，还有“SSS”“SAS”“ASA”“AAS”“HL”等方法.由于全等三角形是相似三角形的特殊情况，判定两个三角形相似除定义外，是否也有类似的判定方法？本节课我们类比研究两个三角形全等的判定方法来研究两个三角形相似的判定方法（.揭示课题）

环节2：探索三角形相似的条件——生成相似三角形判定定理1.

师：有一个角对应相等的两个三角形相似吗？为什么？

生1：不一定相似.例如，含60°角的直角三角形与含45°角的直角三角形不相似.

师：不错.否定结论只要举个反例即可.有两个角对应相等的两个三角形相似吗？

师：若不能肯定或否定的话，请先依次完成下列任务.

（1）在白纸上画一个△ABC.

（2）作一个△A′D′E′，使∠A′=∠A，∠D′=∠B.

（3）议一议：△A′D′E′与△ABC是不是相似三角形？（待学生完成任务）

师：△A′D′E′与△ABC是不是相似三角形？

生2：好像相似.但说不出它们对应边成比例的理由.

师：虽然不能完全肯定，但可以提出这样的猜想：有两个角对应相等的两个三角形相似.下面我们来证明这个猜想是正确的.现在请大家先依次完成下列任务.

（1）在所画的图形上标注已知条件.

（2）结合图形写出已知与求证.

（待学生完成任务）

师：如图1，要证明△A′D′E′∽△ABC，只要证什么？

生3：因为∠A′=∠A，∠D′ =∠B，∠E′=∠C，所以只要证

图1

师：有道理，现在只能依据相似三角形的定义.我们学过的哪个结论与比例线段有关？

生4：由平行线截得的比例线段的基本事实与比例线段有关.

师：好的.如图1，若在△ABC中能作一个△ADE，使△A′D′E′≌△ADE，则要证△A′D′E′∽△ABC，只要证△ADE∽△ABC.能作一个△ADE，使△A′D′E′≌△ADE吗？

生5：能.因为∠A′=∠A，在AB上截取AD=A′D′，作DE∥BC，交AC于点E，则∠ADE=∠B=∠D′，所以△A′D′E′≌△ADE（ASA）.

师：好的.因为DE∥BC，所以可得哪些结论？

生6：因为DE∥BC，所以∠ADE=∠B，∠AED=∠C，

（众生困惑、期待）

，所以△ADE∽△ABC.又△A′D′E′≌△ADE，所以△A′D′E′∽△ABC（相似三角形的传递性）.

师：下面请大家按这样的思路把证明过程完整地写出来.

（待学生完成任务）

师：这样我们得到了如下的相似三角形判定定理1：

有两个角对应相等的两个三角形相似.

师：在证明过程中还可得以下结论（课本中称它为预备定理）：

平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.师：怎样用几何语言来表示相似三角形判定定理1？生7：在△A′D′E′和△ABC中，若∠A′=∠A，∠D′=∠B，则△A′D′E′∽△ABC.

师：好的.请大家课后用几何语言来表示预备定理.证明判定定理1的基本思路是什么？

生8：根据相似三角形的传递性，通过构造全等三角形来证明.

生9：通过构造全等三角形把分散的条件集中起来.

师：有道理.我们根据相似三角形的传递性，用构造全等三角形的方法实现化归.这种化归思想以后会经常用到.

环节3：参与定理应用的活动——合作解决有代表性的问题.

师：现在我们一起解决下列问题.

问题：在一次数学活动课上，为了测量河宽AB，小聪采用了图2所示的方法：从A处沿与AB垂直的直线方向走45m到达C处，插一根标杆，然后沿同方向继续走15m到达D处，再右转90°走到E处，使B、C、E三点恰好在一条直线上.量得DE＝20m，这样就可以求出河宽AB.请你说明理由，并算出结果.

师（稍停顿后）：谁来说明理由并计算其结果？

图2

生10：因为AB⊥AD，DE⊥AD，所以∠BAC=∠EDC=90°.因为B、C、E三点在一条直线上，所以∠ACB=∠DCE.所以△ABC∽△DEC（有两个角对应相等的两个三角形相似），所以又

答：河宽AB是60m.

师：好的.解决这个问题经历了哪几个基本步骤？

生11：先根据已知条件判定两个三角形相似，再用相似三角形的性质来计算.

师：解题的关键是什么？

生12：根据相似三角形的性质列出合适的方程.

师：好的.在几何计算中，经常要运用方程思想.能用同样的道理，再设计几种测量河宽AB的方法吗？请大家合作研讨.

（约4分钟后）

师：谁来汇报设计的方案？

生13：如图3，只要CD∥AB，使A、C、E三点共线，B、D、E三点共线，并量出AC、CE、CD的长、就能求出AB的长.

生14：如图4，在BA的延长线上取点D，在AB的右侧取点C，连接AC，过点D作DE∥AC，交BC的延长线于点E，并量出AC、DE、AD的长，就能求出AB的长.

图3

图4

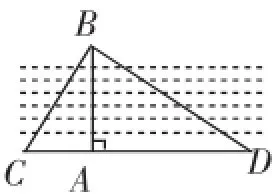
图6

生15：如图5，只要DE∥AB，使A、C、D三点共线，B、C、E三点共线，并量出AC、CD、DE的长，就能求出AB的长.

生16：如图6，只要BA⊥CD，∠C+∠D=90°，并量出CA、AD的长，就能求出AB的长.

师：太有才了！这些都是可行的方法.下面请大家完成课本中的练习题.

（待学生完成任务后教师组织学生交互反馈与评价）

环节4：参与回顾与思考的活动——合作进行反思与总结.

师：本节课研究了哪些内容？

生17：本节课研究了相似三角形判定定理及其应用.

师：好的.我们是怎样研究的？

生18：先探索并证明判定定理1，再用判定定理1解决实际问题.

师：不错.发现判定定理1的策略与方法分别是什么？

生19：策略是分类讨论，方法是画图、推理.

师：好的.这是发现数学结论常用的经验.

师：大家在学习过程中还有哪些收获或体会？

生20：三角形按相似的规则变化时，对应角的度数保持不变.

师：不错.图形的相似具有保持对应角度数不变的性质.

生21：分类讨论是发现数学结论的基本策略.

生22：只要∠A′=∠A，就可以在△ABC中作一个△ADE，使△A′D′E′≌△ADE.

生23：化不熟悉的问题为熟悉的问题是解决问题的重要思想方法.

生24：用相似三角形知识能解决许多实际问题.

生25：用传递性证两个三角形相似时，只要△A′D′E′∽△ADE即可.

生26：尽管测量河宽的方法具有多样性，但要选择简单的方法.

生27：根据相似三角形的性质可列出多个方程，但要选择合适的方程.

师：好！这些收获与体会非常有价值，对后继学习有指导作用.

三、教学分析

探索与证明相似三角形判定定理1的思想方法对后继学习有指导作用.定理的探索与证明的过程和所蕴含的归纳思想、化归思想、演绎思想等，用定理解决实际问题的过程和所蕴含的数形结合思想、方程思想等及测量河宽的多样化设计方案，这些对发展学生的智力、能力和个性有积极的影响.目前在该课的教学中，大多数教师没有体现分类探索的策略；有些教师探索判定定理和证明定理之前的分析过程短暂；大多数教师在获得判定定理和解决实际问题之后缺乏必要的反思；大多数教师在认知过程中没有留给学生充足的自主思考与实践的时间和合作交流的机会.

本课例在“精致化”分析基础上，改变课本先讲预备定理再讲判定定理1的做法，将其教学立意于过程教育，并从学生已有的知识与经验出发，运用教师价值引导与学生自主建构相结合的适度开放的方式，引导学生经历完整的认知过程.在“回顾并提出问题”的教学中，既有回顾研究两个三角形全等的判定的思想方法，以激活研究全等三角形判定的数学活动经验，又有提出问题的过程，以建立新旧知识之间的内在联系和激发学生的学习兴趣.在“探索并证明判定定理1”的教学中，既有借助已有经验进行“分类探索→画图猜想→分析证明→多样表达”的过程，以获得判定定理1和预备定理及发展探索与证明的能力，又有获得判定定理之后的反思，以内化用构造全等三角形来实现化归的思想方法，积累用相似三角形的传递性和构造全等三角形来证三角形相似的新经验.在“定理应用”的教学中，既有引导学生解决给定问题的过程，以巩固所学的知识和发展智慧技能，又有解决问题之后的反思，以认识用相似三角形知识解决实际问题的思想方法，还有开放式设计测量河宽方案的过程，以发展学生的发散思维能力和想象能力，积累测量河宽等方案的数学活动经验.在“回顾与思考”的教学中，既有回顾研究内容，又有回顾研究方法，还有学生谈学习后的收获与感受.

参与研修的教师普遍认为，本课例遵循了定理教学的基本规范，体现了过程教育和以学为中心的思想，统筹兼顾了过程与结果，能实现教学目标.一般地，定理教学要经历“提出问题→操作观察→归纳猜想→验证或证明→多样表达→解决问题→反思内化”的过程，并在组织实施数学活动时，留给学生足够的自主思考与实践的时间和合作交流的机会，发挥教师在数学活动中的主导作用，合理评价学生在数学活动过程中的表现，以促使学生对定理的认识达到一定的“深度”和“宽度”，促使学生学会主动提出问题，独立思考问题，合作探究问题，以及养成敢于质疑、善于表达、认真倾听、勇于评价和不断反思的良好品质和习惯.

教学实践表明，在定理教学中，要实现知识、技能、能力、态度的完美统一，需要教师增强揭示定理所蕴含的思维活动过程的自觉性，而引导学生经历实质性思维过程需要教师充分贯彻启发式教学思想.以符合“最近发展区”理论的题材为载体，从学生已有的知识与经验出发，运用教师价值引导与学生自主建构相结合的适度开放的方式，能使学生经历过程中的思维站点，从而能促进学生全面、和谐发展.本课例在农村中学实施后，发现时间有点儿紧张，可见体现过程教育的课堂教学会对按时完成教学任务带来挑战.解决这个问题的策略：一是运用课内外结合的方法——课前预习教师设计的“导学案”；二是根据学生的现实来确定过程与结果的平衡点——结果是主要的、基本的，相对来说过程是次要的、从属的.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.

2.范良火.义务教育教科书数学（九年级上册）［M］.杭州：浙江教育出版社，2014.