初中数学一次函数品质课堂的打造

☉浙江绍兴市越城区皋埠中学赵增良

初中数学一次函数品质课堂的打造

☉浙江绍兴市越城区皋埠中学赵增良

一、引言

一次函数是初中数学教学的重、难点，对于学生今后反比例函数和二次函数的学习具有重要意义.在组织课堂教学活动的过程中，教师一定要重视对一次函数的教学，以为学生将来的数学学习奠定基础.当前初中生在一次函数学习过程中表露出来一些问题，教师在课堂教学设计中要根据学生的认知水平，合理组织教学活动，有的放矢解决教学过程中存在的问题.

二、现阶段打造高品质一次函数课堂教学遇到的问题

1.教师.

教师是课堂教学的主导，教师的教学理念、所采用的教学手段都对课堂教学质量的最终提高有着至关重要的影响.在开展一次函数课堂教学活动的过程中，由于教师教学观念的落后、教学手段的不科学，导致学生对一次函数学习不感兴趣，灌输式教育挫伤了学生学习的积极性.

2.学生.

初中生的思维尚处于形象思维阶段，一次函数是学生第一次接触函数问题，很多学生一时之间难以理解抽象的函数概念，不善于掌握自变量与因变量之间的关系，导致学习频频遇到挑战.重压之下，很多学生逐渐丧失学习信心，从某种程度上说，这对教学质量的提高造成了一定阻碍.

三、如何打造一次函数品质课堂

1.精心设计例题导入概念.

初中一次函数知识主要包括函数和一次函数的定义、一次函数的图像与性质、确定一次函数的表达式、一次函数图像的应用等内容，这其中，以利用待定系数法确定一次函数的解析式，一次函数与二元一次方程组、一元一次不等式的关系，用一次函数解决实际问题这些内容为重点和难点.在组织教学活动的过程中，教师应当按照学生的实际认知水平，循序渐进推进教学.

在讲解函数与一次函数的定义这一知识时，为帮助学生辨别正比例函数与一次函数的概念这一内容，教师可以设计这样的例题：

例1写出下列各题中y与x之间的关系式，并判断：y是否为x的一次函数？是否为正比例函数？

（1）汽车以60千米/时的速度匀速行驶，行驶路程y（千米）与行驶时间x（时）之间的关系；

（2）圆的面积y（cm2）与它的半径x（cm）之间的关系；

（3）一棵树现在高50厘米，每个月长高2厘米，x月后这棵树的高度为y厘米.

解析：（1）y=60x，y是x的一次函数，也是x的正比例函数.

（2）y=πx2，y不是x的正比例函数，也不是x的一次函数.

（3）y=2x+50，y是x的一次函数，但不是x的正比例函数.

在讲解利用待定系数法确定一次函数解析式这一知识时，教师可以设计这样的例题：

例2已知一次函数y=kx+b（k≠0），当x=1时，y=5，且它的图像与x轴的交点的横坐标是6，求这个一次函数的解析式.

解析：待定系数法主要有四步：设、代、解、还原.根据待定系数法，将x=1、y=5和x=6，y=0分别代入y=kx+b，得

所以一次函数的解析式为y=-x+6.

教师可以在课堂上随机抽取几位学生进行提问，一方面，这可以使学生集中注意力听课，加深学生对一次函数和函数的定义、利用待定系数法确定一次函数的解析式等知识的理解；另一方面，通过学生的答案，教师得以掌握学生对这些概念的理解情况，从而适时根据学生的学习情况调整教学计划.

2.从生活角度切入函数问题.

初中学生的思维尚停留在感性思维阶段，形象思维活动占据主导地位，抽象思维能力有待进一步发展.一次函数的学习，恰恰是对学生抽象思维的一次挑战，考虑到学生第一次接触函数内容，为帮助学生更好地理解抽象性函数知识，教师不妨从学生身边的话题引入教学，采用生活教学法激发学生对数学的兴趣.

例如，在讲解函数的定义这一知识的过程中，为充分凸显“唯一确定”这一概念，教师可以鞋码中的“码数”与“厘米”之间的换算关系进行导入：

例3下表是对本班同学所穿的鞋码的统计：

如果用y来表示鞋的码数，x表示鞋的长度，那么，不论如何变化，对于每一个确定的鞋的长度值，都有唯一确定的码数值与其相对应，这就是函数唯一确定的概念.

初中数学新课程教学标准提出“数学来源于生活”这一理念，教师从生活角度进行切入，可以使学生感觉到课本上所学习的函数概念与生活中的实际问题相互联系在一起，容易在学习过程中产生亲切感，有助于教学活动的顺利开展.

例4已知在△AOB中，∠B=90°，AB=OB，点O的坐标为（0，0），点A的坐标为（0，8），点B在第一象限内，将这个三角形绕原点O旋转75°，那么旋转后点B的坐标为___________.

很多学生乍看这道题，觉得既涉及旋转，又涉及三角形、象限，完全一头雾水、不知所措.此时，掌握数形结合思想，巧妙使用图像帮助解题就显得非常重要.在讲解本题的过程中，教师可以指导学生画出△AOB在平面直角坐标系内的图像，问题就迎刃而解了.

解析：根据题目当中的已知条件画图（如图1）.

因为OA=8，∠B=90°，AB= OB，△AOB是等腰直角三角形，

图1

△AOB绕原点O旋转75°可能是逆时针旋转，也可能是顺时针旋转，对这两种情况分别分析可知：

①逆时针旋转时，过点B′作B′C′⊥y轴于C′.

因为旋转角为75°，所以∠B′OC′=75°-45°=30°.

②顺时针旋转时，过点B″作B″C″⊥x轴于C″.

因为旋转角为75°，所以∠B″OC″=75°-45°=30°.

（2016四川）小明和爸爸从家步行去公园，爸爸先出发一直匀速前行小明后出发，家到公园的距离为2500m，图2是小明和爸爸所走的路程s（m）与步行时间t（min）的函数图像：

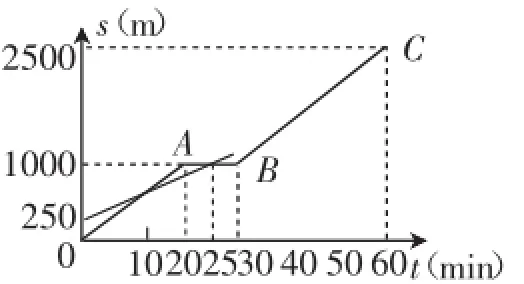
图2

（1）直接写出小明所走路程s与时间t的函数关系式；

（2）小明出发多少时间与爸爸第三次相遇？

（3）在速度都不变的情况下，小明希望比爸爸早20min到达公园，则小明在步行过程中停留的时间需作怎样的调整？

以上所举的几个例子都是数形结合类例子，反映了从“数”到“形”思想的应用.纵观当前中考一次函数数形结合类题目，以形变数、以数化形都有涉及.教师应当有效开展这两类题型的训练，提高学生运用数形结合思想的能力.一次函数教学离不开了图像，学生整个数学学习生涯离不开数形结合思想.课堂教学活动组织过程中渗透数形结合思想，对于学生日后数学课程的学习有重要意义.通过以形助数或以形解数，可以将抽象问题形象化，复杂问题简单化，从而达到优化教学过程、升华学生学习品质的目的.

新课程形势之下，教师需要对传统进行审视与选择，如何将复杂抽象的概念、定义教得有滋有味，值得每一位数学教师永恒探讨.

1.中华人民共和国教育部.全日制义务教育数学课程标准［S］.北京：人民教育出版社，2011.

2.罗小伟.中学数学教学论［M］.广西：广西民族出版社，2016.

3.黄海东.《一次函数》测试题［J］.中学生数理化（八年级数学），2010（10）.

4.陈金龙.一次函数的图像教学案例［J］.新课程（下），2011（3）.