例谈平面几何知识在圆锥曲线中的应用

例谈平面几何知识在圆锥曲线中的应用

☉江苏省常熟浒浦高级中学 李艳华

解析几何是代数与几何的完美结合，圆锥曲线问题一般兼有深刻的几何背景和灵活多变的代数结构，这类问题经常困扰着学生.既然有些圆锥曲线问题有一定的几何背景，那么平面几何的常规方法在解决这类问题的过程中能不能起到一定的辅助作用呢？回答是肯定的.我们在使用代数方法研究曲线性质的同时，可以辅以平面几何的方法，真正实现数与形的结合.

本文主要想展示平面几何方法在解决圆锥曲线的各类问题中的应用，其辅助功能可以体现在以下几个方面.

一、解决距离和的最值问题

例1已知抛物线C：y2=8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若，则|QF|=（）.

分析：此题可以用代数方法解决.

本题也可以利用抛物线的定义巧妙地利用三角形相似来做，这应该也是出题者的用意所在.

解法二：如图1，过Q点向准线l作垂线，垂足为H，设|QF|的长度为x.由抛物线的定义知，|QH|=|QF|=m，，FG=4，利用△PHQ～△PGF，得到，所以m=3.

图1

二、解决切线斜率问题

例2已知点A（-2，3）在抛物线C：y2=2px的准线上，过点A的直线与C在第一象限相切于点B，记C的焦点为F，则直线BF的斜率为（）.

图2

解析：如图2，过B作准线的垂线BD，D为垂足，AB为抛物线的切线.由抛物线的光学性质知，∠DBA=∠FBA，又|BF|=|BD|，

所以△BFA≌△BDA，

所以BF⊥AF，F（2，0），

点评：在解决圆锥曲线的客观题中，偶尔使用圆锥曲线的光学性质也可以收到比较好的效果.

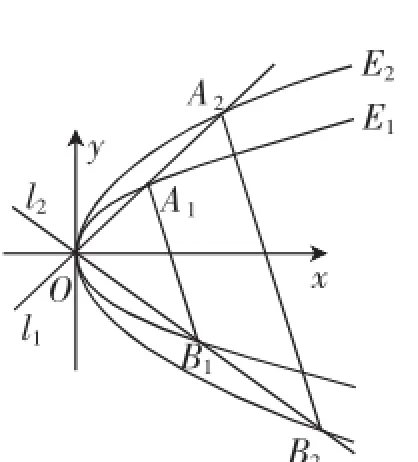
图3

三、解决面积问题

例3如图3，已知两条抛物线E1：y2=2p1x（p1＞0）和E2：y2=2p2x（p2＞0），过原点O的两条直线l1和l2，l1与E1，E2分别交于A1，A2两点，l2与E1，E2分别交于B1，B2两点.

（1）证明：A1B1∥A2B2；

（2）过原点O作直线l（异于

l1，l2）与E1，E2分别交于C1，C2两点，记△的面积分别为与，求的值.

解析：试题所给的参考答案中对此题的解决也是利用了几何方法，笔者给出进一步的优化方法.

（1）证明：由A1，A2，B1，B2向x轴作垂线，垂足为A3， A4，B3，B4，如图4所示，要证A1B1∥A2B2，只需证B1B3，B2B4表示的是A1，A2，B1，B2点的纵坐标的绝对值，故只需联立直线与抛物线求出交点的纵坐标即可.

设直线l1，l2的方程分别为y= k1x，y=k2x，与抛物线方程联立可得A1，A2，B1，B2点的纵坐标的绝对值分别为

所以A1B1∥A2B2.

（2）如图5，由第（1）问知，A1B1∥A2B2，同理可以得到A1C1∥A2C2，B1C1∥B2C2，故△A1B1C1～△A2B2C2，故

在本题的解决中，第（1）问利用了相似三角形的转化来证明平行，相对于利用向量共线或是斜率相等来证明,计算量减少了；第（2）问通过边平行来证明相似，利用了空间中的等角定理.此题在出题时少了纯粹的代数计算，加深了几何分析的过程，符合高考更注重对学生思维考查的命题趋势.

图5

四、解决与圆有关的问题

图6

（1）求椭圆C的方程；

（2）过左焦点F1的直线交椭圆于M、N两点，交直线x=-4于点P，设，试证λ+μ为定值，并求出此定值.

本题笔者在讲授时仍然采用常规的方法，方法如下：

解：（1）由四边形F1B1F2B2的内切圆半径为用等面积法可以得到

（2）根据已知条件可设直线MN的方程为y=k（x+1），代入椭圆方程，整理得

（3+4k2）x2+8k2x+4（k2-3）=0.

设M（x1，y1），N（x2，y2），则

所以λ+μ=0为定值.

对于第（2）问，有的学生就提出疑问：相关点均位于直线l上，能不能构造三角形利用相似边成比例来进行求解.笔者便鼓励他们做下去，学生1便作出了下面的图7，但接着就不知该如何进行下去了，笔者提示他两点：①既然想通过三角形相似来找λ，μ的关系，这里面可以用哪一个比例关系？②能不能通过题目中的向量关系式，把各条边均用同一个参数来表示？

图7

学生在我的提示之下，给出了下面的解法：

第（2）问解法二：如图7所示，x=-4为椭圆的准线，过M、N作准线的垂线，垂足为Q、R，不妨设MF1=m，（μ＜0），得.由椭圆的第二定义知，MQ=2m带入可得λ+μ=0.题目得证.

初中数学中的几何与高中数学几何知识不应该是相互割裂的状态，教师如果能够适当地引导学生，可以让学生的解题思路更为宽广，从而会有意想不到的收获.某些圆锥曲线问题使用平面几何方法处理以后，有的可以使圆锥曲线的定义得到灵活应用，有的可以利用圆锥曲线本身的几何性质简化过程，有的可以直接深入到几何本质，有的可以通过几何途径将问题作有效转化，总之几何方法使用得当就可以避开繁难的代数运算，使数与形完美结合，使复杂问题简单化，抽象问题具体化，从而使问题得到有效解决.