红莲与白藕，原来是一家———对源于教材的两道高考题的研究与思考

红莲与白藕，原来是一家
———对源于教材的两道高考题的研究与思考

☉河北省昌黎第一中学 田卫东

众所周知，数学教材是数学学科的核心教学材料，它是几代数学工作者智慧的结晶，不仅具备完整的知识体系，更有强大的权威性，同时也是教师实施教学和学生学习的主要材料.命题者在命制试题时，都会对教材予以高度关注，高考的部分试题便是从教材中选取优秀例题或习题进行加工、改造而成.笔者经历了2013和2016两年的高三复习与高考，巧合的是在这两年的全国新课标卷Ⅰ的数学试题中，出现了两道非常相似的题目，更重要的是，它们均来自于人教社的新课标实验教材.现将这两道题以及对它们进行的简单变化呈献给读者，以引起广大教师和学生的注意，在平时的教学和高三的复习过程中，一定要重视教材，尤其要重视对教材中经典题目的深入研究，避免陷入“题海”中而不能自拔.

一、两道试题与教材习题的比较

（1）已知圆M：（x+1）2+y2=1，圆N：（x-1）2+y2=9，动圆与圆M外切并且与圆N内切，圆心P的轨迹为曲线C，求C的方程.（2013年全国新课标卷Ⅰ第20题）

（2）设圆x2+y2+2x-15=0的圆心为A，直线l过点B（1，0）且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E，证明：|EA|+|EB|为定值，并写出点E的轨迹方程.（2016年全国新课标卷Ⅰ第20题）

解答过程如下：

解：（1）如图1，设圆P的半径为R，圆M与圆N的半径分别为r1，r2，因为圆P与圆M外切且与圆N内切，所以|PM|+|PN|=（r1+R）+（r2-R）=r1+r2=4，由椭圆的定义可知，曲线C是以M、N为左、右焦点，长半轴长为2，短半轴长为的椭圆（左顶点除外），其方程为+=1（x≠-2）.

图1

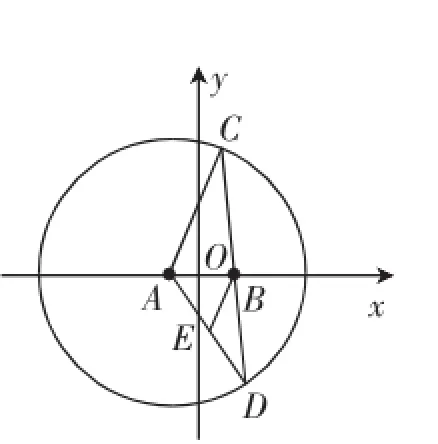
图2

（2）如图2，因为AD=AC，EB∥AC，故∠EBD=∠ACD=∠ADC，所以|EB|=|ED|，所以|EA|+|EB|=|EA|+|ED|=|AD|.因为圆A的标准方程为（x+1）2+y2=16，所以|AD|=4，所以|EA|+|EB|=4.

由题意知，A（-1，0），B（1，0），|AB|=2，根据椭圆定义可得点E的轨迹方程为+=1（y≠0）.

再给出普通高中课程标准实验教科书《数学》选修2-1中第50页B组题的第2题及第49页A组题的第7题：

（3）一个动圆与圆x2+y2+6x+5=0外切，同时与圆x2+ y2-6x-91=0内切，求动圆的圆心轨迹方程，并说明它是什么样的曲线（.答案为+=1，它是以（-3，0）和（3，0）为焦点的椭圆）

（4）如图3，圆O的半径为定长r，A是圆O内一个定点，P是圆上任意一点.线段AP的垂直平分线l和半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是什么？为什么？

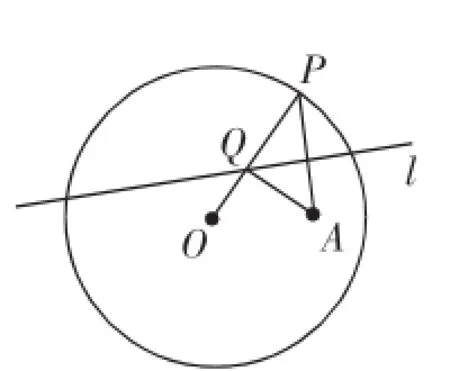
图3

简解（4）：因为l是线段AP的垂直平分线，所以PQ= AQ，所以QO+QA=QO+QP=OP=r.根据椭圆的定义可知，点Q的轨迹是以O、A为焦点，长轴长为r的椭圆.

不言而喻，其中的关系已经非常明显，第（1）题是在第（3）题的基础上，将两个定圆内含改为了内切，同时改变了另外的一些数据，但题目的本质并没有发生任何变化；第（2）题则是在第（4）题的基础上编制而来的.

二、两道试题原是“一家人”

我们看第（3）题，如图4，其解答过程与第（1）题相同.若将题中条件适当改变，则可以得到：

变化1将圆M改为点M，则问题变成圆P经过定点M，且与圆N相内切，求圆心P的轨迹.

图4

图5

简解：如图5，|PM|+|PN|=r=10，则点P的轨迹是以M、 N为焦点的椭圆，其方程为

变化2在变化1中，延长至切点Q，连接MQ，则点P在线段MQ的垂直平分线上，如图6.改变一下叙述方式，即圆N的半径为r，M是圆N内不同于N的一个定点，点Q是圆N上的任意一点，线段MQ的垂直平分线l和半径NQ相交于点P，求点P的轨迹.此题即成为了第（4）题.

简解：因为直线l是线段MQ的垂直平分线，所以| PM|=|PQ|，所以|PM|+|PN|=|PQ|+|PN|=r=10，所以点P的轨迹是以M、N为焦点的椭圆，其方程为

图6

变化3在变化2中，如图7，将QM延长交圆N于点E，连接EN，过M作EN的平行线交NQ于点P，求点P的轨迹.这就是2016年全国新课标Ⅰ卷第20题的第（1）问.

简解：因为|NE|=|NQ|，EN//MP，所以∠QEN=∠EQN=∠QMP，所以|PM|=|PQ|，所以|PM|+|PN|=|PQ|+|PN|=r=10，所以点P的轨迹是以M、N为焦点的椭圆（去掉长轴端点）.

事实上，无论哪种变化，其本质都是考查对平面内动点与两个定点距离之和为常数的深刻理解，只不过都是以圆为载体，借助圆心为定点和半径为定值这两个条件，通过平面几何的有关定理及推论，而达到利用椭圆的定义探究动点轨迹的目的.从这个角度来说，它们的确是“一家人”.稍作改动，还可以得到以下题目：

变式已知圆O的方程为x2+y2=4，点A（，0），以线段AB为直径的圆内切于圆O，求动点B的轨迹方程.

三、它们还有“兄弟姊妹”

接下来，我们再看这样一道题：

（5）如图8，与两圆x2+ y2=1及x2+y2-8x+12=0都外切的圆的圆心在（）.

A.一个椭圆上

B.双曲线的一支上

C.一条抛物线上

D.一个圆上

图8

这是普通高中课程标准实验教科书《数学》选修2-1第80页的复习参考题A组第3题的第（2）题.

该题目的解法如下：圆x2+y2=1的圆心为F1（0，0），圆x2+y2-8x+12=0的圆心为F2（4，0），动圆的圆心为M，半径为r，则|MF1|=r+1，|MF2|=r+2，故|MF2|-|MF1|=1，结合双曲线的定义可知，所求动圆圆心的轨迹是双曲线的左支，故正确答案为B.

将此题的条件稍作改变，即可得到：

变化1将题中的与两圆都外切改为都内切，即圆M与圆F1和圆F2都内切，试确定圆心M的轨迹.

简解：设动圆的圆心为M，半径为r，则|MF1|=r-1，|MF2|=r-2，则|MF1|-|MF2|=1.由双曲线的定义可知，所求动圆圆心的轨迹是双曲线的右支.

由此可见，将第（5）题中的动圆与两定圆都外切改为动圆与两定圆都相切，则动圆圆心的轨迹即为完整的双曲线.

变化2将圆F1改为点F1，则问题变为圆M经过定点F1，且与圆F2相外切，试确定圆心M的轨迹.

简解：设动圆的圆心为M，半径为r，则|MF2|-|MF1|=r+2-r=2.由双曲线的定义可知，所求动圆圆心的轨迹是双曲线的左支.

说明：若将此题中的外切改为内切，即可得到该双曲线的右支.

变化3在变化2中将圆M与圆F2的切点记为P，题目可叙述为：P是圆F2上的任意一点，F1是圆外的一个定点，线段PF1的垂直平分线l和直线PF2相交于点M，当点P在圆上运动时，求点M的轨迹.此问题即为《数学》选修2-1第62页的A组第5题.

简解：如图9，因为直线l是线段PF1的垂直平分线，所以|MF1|=|MP|，所以|MF2|-|MF1|=|MF2|-|MP|=2，所以点M的轨迹是双曲线的左支.

说明：①当线段PF1与圆相切时，则有l∥PF2，所以点M不存在；②设直线PF1与圆相切时的切点分别为P1、P2，当点P在P1、P2之间的优弧上运动时，点M的轨迹是双曲线的右支.

变化4在变化3的基础上，我们还可以这样改动：P是圆F2上的任意一点，F1是圆外的一个定点，直线PF1与圆F2交于点E，连结EF2，过点F1作F1M//F2E与直线MF2交于点M，试确定M的轨迹.

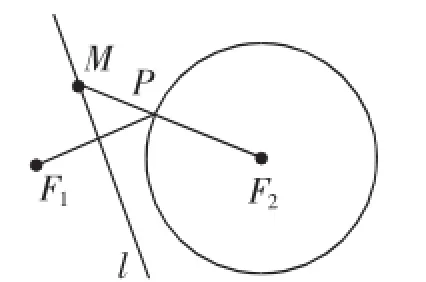
图9

图10

简解：如图10，因为|PF2|=|EF2|且F1M//F2E，所以∠F2EP=∠EPF2=∠MPF1=∠MF1P，所以|MF1|=|MP|，所以|MF2|-|MF1|=|MF2|-|MP|=|PF2|=2，所以点M的轨迹是双曲线的左支（去掉顶点）.

说明：①当线段PF1与圆相切时，点M不存在；②设线段PF1与圆相切时的切点分别为P1，P2，当点P在P1，P2之间的优弧上运动时，点M的轨迹是双曲线的右支（去掉顶点）.

变化5将圆F1改为点F1，将圆F2视为一条与x轴垂直的直线，于是可以得到以下问题：已知F1是直线l外的一个定点，圆M经过点F1且与直线l相切，试确定圆心M的轨迹.

简解：设圆M与直线l的切点为N，则|MF1|=|MN|，所以点M的轨迹是以M为焦点，l为准线的抛物线.

如此看来，通过圆与圆的位置关系，以及对它们进行的各种变化，不仅可以得到动点的轨迹是椭圆，也可以是双曲线、抛物线，三种曲线通过这种方式又聚到了一起，可谓“不是一家人，不进一家门”.

变式已知圆O的方程为x2+y2=1，点A（，0），以线段AB为直径的圆C与圆O相切，求动点B的轨迹方程.

四、一点启示与思考

对于第（1）题本文并未展开深入的讨论，如果将所给的两个定圆按照相离、外切、相交、内切、内含这五种位置关系，利用动圆与定圆的内切或外切，我们可以得到各种有关椭圆与双曲线的轨迹，在此不再赘述，有兴趣的读者可以自行研讨.本文的主要目的在于呼吁和提醒努力拼搏在高三前线的的广大师生，教材是我们的学习之本，其中有非常多的经典好题，我们在复习过程中应该重视对它们的整理和研究，结合历届高考试题，也许我们可以找到一些高考命题的规律或思路，同时也可以对教材中的重点知识有更深刻的理解和感悟.本文中的各种变化充分地反映了对椭圆、双曲线、抛物线定义的深入理解，这些问题的解决也相当于完成了这三种圆锥曲线定义的复习，这样的学习或者复习方式会使得我们对这几种圆锥曲线的辩证统一有更加深入的认识，同时也培养了学生的发散思维和思考探究、解决问题的能力，可谓一举数得.作为一名数学教师，应带领学生走出题海，认真钻研教材，改变目前在教学中普遍存在的重资料、轻教材，重过程、轻结果，重数量、轻质量的学习弊端，正如课标中所要求：“要全面提高学生的数学素养，培养学生勤于思考的习惯，坚忍不拔的意志和勇于创新的精神.”