小学生数学认知能力培养策略探析

【摘要】认知能力的培养不仅影响学生数学学习的过程和结果，也影响他们今后数学能力的形成和发展。小学阶段是学生数学思维发展的关键期，也是其数学认知能力形成的重要阶段。在课堂上，教师要遵循规律，完善学生的认知结构；掌握元认知策略，教给学生思维方法；培养学生的兴趣，提高其自我效能感。

【关键词】小学数学；认知能力；认知结构；元认知策略；自我效能感

【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009（2016）60-0038-03

【作者简介】高文萍，南京市银城小学（南京，210036），二级教师。

数学学习是学生原有的认知结构和新的学习内容相互作用，进行同化和顺应，并以此为基础形成新结构的过程。因此，认知能力直接影响学生的数学学习效率及其数学素养的养成。那么，如何培养学生的数学认知能力呢？

一、遵循规律，完善学生的认知结构

美国教育心理学家布鲁纳认为：一门学科知识的学习就是在学生头脑中形成一定的知识结构。学生的认知结构是认知能力形成的基础，在教学中应从多方面加以完善。数学认知结构是数学知识结构与学生心理结构相互作用的产物，是一个具有内部规律的整体结构。

1.遵循认知发展规律，完善学生的认知结构。

现代教学理论强调学生的主体作用和教师的主导作用，教学应充分尊重学生的天性，尊重他们已有的认知和经验。数学教学活动应激发学生的兴趣，调动他们探索的积极性，找准他们的“最近发展区”，将抽象的规律放在具体的情境和实际问题中，让学生在体验和探索过程中发现乐趣，引发数学思考，提升思维能力和创新能力。例如：教学苏教版四下《乘法分配律》一课，教师创设买5件夹克和5条裤子、6件短袖衫和6条裤子这两种情境，让学生列出两组算式。

（1）观察猜想。

师（板书：65×5+45×5=（65+45）×5，32×6+45×6=

（32+45）×6）：观察刚才得出的这两组式子，你有什么发现？能大胆地提出一个猜想吗？

（2）探究验证。

探究要求：

①选择自己喜欢的三个数。

②算出其中任意两个数和第三个数的乘积再相加的结果。

③算出这两个数的和再与第三个数相乘的结果。

④比较两次结果。

⑤小组交流探究结果。

⑥全班汇报，补充实例。

（3）总结提炼。

师：通过不完全举例，可以得出什么结论？

生：两个数的和与一个数相乘，可以用这两个加数分别与这个数相乘，再把两个积相加，结果不变。

师：对，这就是乘法分配律。

在提出猜想、探究验证、总结提炼的过程中，学生参与其中，积累了丰富的素材和活动经验。同时，学生的认知结构得到了完善，从原先的模糊猜想到形成概念再到外化成简练的表达，学生感悟到了操作的乐趣，收获了思维成长的喜悦。

2.充分感知知识发生的过程，加强认知理解。

数学教学是一种思维教学，教师应引导学生“重蹈人类思维发展中的那些关键性步子”。教学苏教版二上《认识厘米》，学生第一次接触长度单位，教师可以这样设计教学。

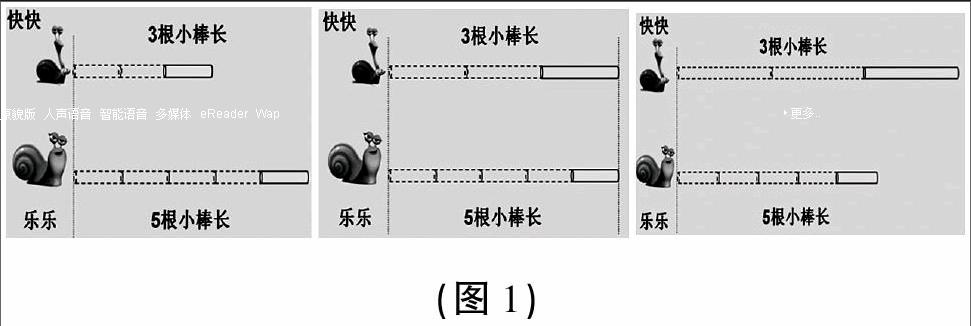
师：瞧，蜗牛快快和乐乐在训练，他们想看看自己1分钟能跑多远。快快跑了3根小棒长，乐乐跑了5根小棒长。谁跑得远？为什么？

生（异口同声）：乐乐跑得远，因为5比3大。

教师肯定了学生的分析，但不急不缓地追问：有不一樣的想法吗？你是怎么想的？

学生开始思考有没有其他情况。

生1：快快和乐乐跑得一样远。

立刻有学生反驳，教师请生1说说理由。

生1：如果快快的小棒短，而乐乐的小棒长，就可能会这样。

全班学生开始思索，越来越多的人点头认同。

见此情景，教师继续追问：她的回答有道理吗？你有没有得到什么启发？

一石激起千层浪，学生很快想到：如果快快的小棒再长一些，快快也可能跑得比乐乐远。

教师出示上述3种情况（如图1），帮助学生形成完整的思路，继续引导学生思考：为什么会出现3种情况？

学生在讨论中发现：比较长短不仅要比数的大小，还要看他们测量用的小棒的长度。小棒长度不同，测量的标准不同，就无法比较结果。

教师抓住这一契机，总结：在测量物体长度时，得有一个统一的标准，这就是长度单位。

从异口同声的“嗯”，到不一样的声音“咦”，再到学生有理有据的辩驳，最终启发的火花在他们思维中闪耀，学生的思维经历了一致、矛盾、否定、修正和完善的过程，从而加强了认知理解，完成了对新知的主动建构。

3.操作验证，拓展数学认知结构。

新课标指出：动手实践、自主探索与合作交流是学生学习数学的重要方式，学生的数学学习活动应当是一个生动活泼的、主动的和富有个性的过程。小学生的抽象和概括能力较弱，教师应鼓励学生在动手实践、自主探索、合作交流中拓展认知结构。教学苏教版一下《两位数加减两位数》，在探索“45+31”时，学生通过摆小棒计算结果，一边摆一边说：“先摆4捆带5根，再摆3捆带1根。”摆好后，学生指着小棒说：“先算40+30=70，再算5+1=6，所以结果是76。”拨计数器时，学生边拨边说：“先拨45，十位上拨4颗珠，个位上拨5颗珠；再拨31，十位上拨3颗珠，个位上拨1颗珠，所以合起来是76。”学生边操作边思考，学习效果显著。因此，操作验证能让抽象变具体。教师应关注学生的动手实践，让学生在积累数学经验的过程中拓展认知结构，提升思维能力。

二、掌握元认知策略，教给学生思维方法

元认知是对自身认知活动的认知，包括对当前正在进行的认知过程和自我认知能力以及两者相互作用的认知。教师应重视运用元认知策略，教给学生学习的方法，这有助于提高学生自主学习数学的能力。例如：教学苏教版四下《解决问题的策略：画图》，教师出示题目：有一块长50米、宽40米的长方形花圃，长和宽都增加了10米，面积增加了多少平方米？

生1：10×10。

生2：50×10+40×10。

生3：（50+10）×（40+10）-50×40。

师（问生3）：你是怎么想的？

生3结合图形讲解。

师：生1和生2分别求的是图中的哪部分？通过刚才的解题，你有什么感受？

在具体情境中，学生自然而然地体会到应用画图策略解决问题的优势，通过反思主动将新知识内化、理顺，以后，他们就会自发地运用画图策略来解决复杂的图形面积计算问题，从而化繁为简，建构新的、良好的认知结构。

三、培养学生的兴趣，提高其自我效能感

现代教学理论强调学生的主体作用和教师的主导作用，教学应充分尊重学生天性，培养学生的学习兴趣。新课标指出：数学教学活动应激发学生兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维。教师要解放思想，树立民主、平等的教育观念，给学生营造一个敢想、敢说、敢做的大舞台。数学游戏和有趣的情境恰恰迎合了学生思维发展的需要，它不仅能提升学生的学习兴趣，还能增强学生的体验性，激发他们学习的积极性、主动性，使学生获得成就感，提高自我效能感。例如：教学苏教版一上“认识10以内的数”单元后，教师自编了数学游戏——“数字魔法师：数字变变变”。

（1）移动一根小棒。

师：下面老师来给大家变个魔术。（出示：）这是数宝宝3。（课件移动一根小棒，变成“5”）现在变成数宝宝5了，我是怎么变的？

生：移动了一根小棒。

师：他提到了一个词“移动”，你能像这样把数宝宝3变成数宝宝5吗？想一想，还能把3变成几呢？自己变一变。

生：可以变成2。

师：真神奇！还有这样的数宝宝吗？

生1：6移动一根变成9，还能变成0。

生2：9移动一根变成6，还能变成0。

生3：数宝宝0变成6，也能變成9。

师：看来，数宝宝0、6、9都是有魔力的数，它们可以相互变变变。

（2）添上或拿走一根小棒。

师：我们换一种玩法，把其中一个数宝宝添上一根或拿走一根，能不能变成其他的数宝宝呢？先试一试，再和同桌说一说。

生1：1添上一根变成7，7拿走一根变成1。

生2：3添上一根变成9，9拿走一根变成3。

生3：5添上一根变成6，6拿走一根变成5。

生4：0添上一根变成8，8拿走一根变成0。

师：8拿走一根还能变成几？还有吗？

生：还能变成9、6。

（3）我的游戏我做主。

师：刚才我们通过移动、添上或去掉一根小棒，使一个数字变成了另一个数字，我们还可以怎么变？

生：添上两根小棒……

师：游戏规则是可以变化的，请你想一个游戏规则，和同桌玩一玩。

游戏情绪的渲染和调动，使学生感受到数学的乐趣，增强了他们学习的信心。

在小学数学教学中，培养学生的认知能力是一个长期的过程。在数学课堂中，教师提出的问题或任务要适合学生的认知发展水平，让学生在积极参与中积累经验，在师生对话、生生对话以及操作验证中碰撞思维，享受学习的乐趣，让数学思维在学生的心田悄然开花、结果。