包含q-psi函数的函数完全单调性及其应用
汪韩,王连堂
(西北大学数学学院,陕西 西安 710127)
包含q-psi函数的函数完全单调性及其应用
汪韩,王连堂
(西北大学数学学院,陕西 西安 710127)
主要证明了涉及q-digamma函数的完全单调性.通过引入经典q-理论将包含digamma函数的函数进行q-模拟,利用q-模拟函数以及级数的性质,得到了包含q-digamma函数的完全单调性.最后利用它们的完全单调性得到了有关q-digamma和q-trigamma函数的不等式.
完全单调;q-模拟;q-psi函数;不等式;q-trigamma函数
1 引言
Gamma函数与psi(digamma)函数在x>0时的定义为:
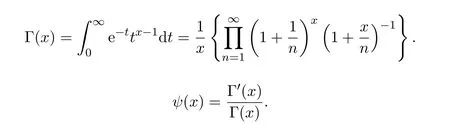
psi函数是Gamma函数的对数导数,psi函数的各阶导数ψ(i)(x)对于i∈N, N={1,2,3,…},被称为polygamma函数在文献[1]中,定义了x>0时.Gamma函数的q-模拟
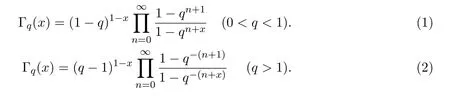
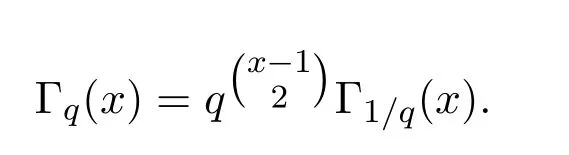
q-psi函数为q-Gamma函数的对数导数,
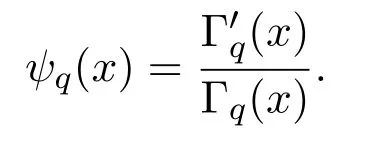
psi函数和q-psi函数被包含在很多不等式中,见文献[2-3],由(1)和(2)可以得到如下:
当0<q<1且x>0,
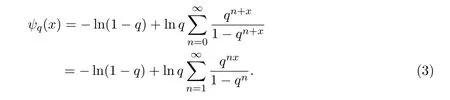
当q>1且x>0,
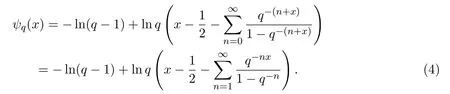
ψ(k)(x)的q-模拟为k∈N,被称为q-polygamma函数,其中和分别被称为q-trigamma函数和q-tetragamma函数对(3)式两边取对数后求导可得,当q>0时,有
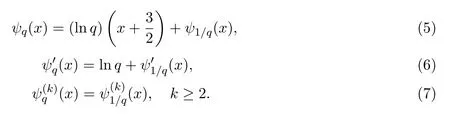
文献[4-5]中介绍了gamma函数及psi函数和它们的q-模拟之间的关系.
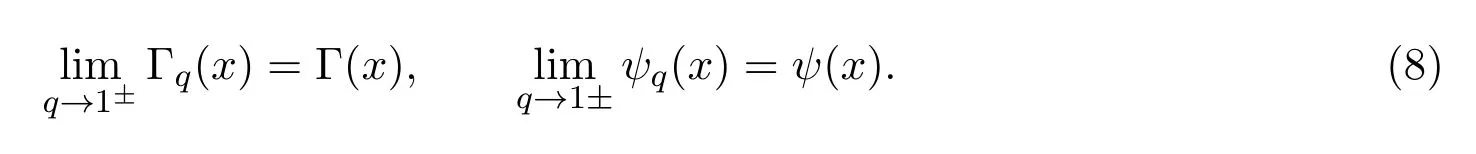
更多关于q-gamma函数的内容,见文献[6-8].
直接从套管出口引出天然气并加以综合利用,见图4。套管气利用情况:套管气在加热炉中燃烧,加热输油管线或掺水;套管气用于单井天然气发电机发电。
文献[9-10]给出了完全单调性的定义:一个函数f被称为区间I上的完全单调函数,如果f在区间I上的各阶导数满足对于任意的x∈I且n≥0,有(−1)nf(n)(x)≥0.
完全单调函数在各个分支学科都有应用,如,解析数论、概率论、物理学,见文献[11-13].文献[14]证明了函数
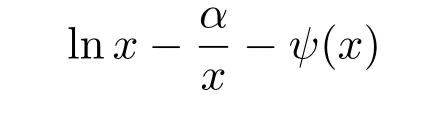
在(0,∞)上是完全单调的,当且仅当
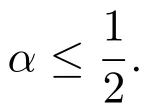
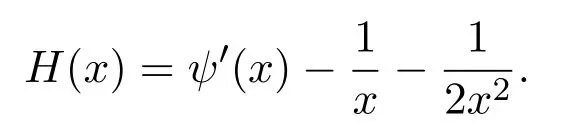
当x>0时,定义函数
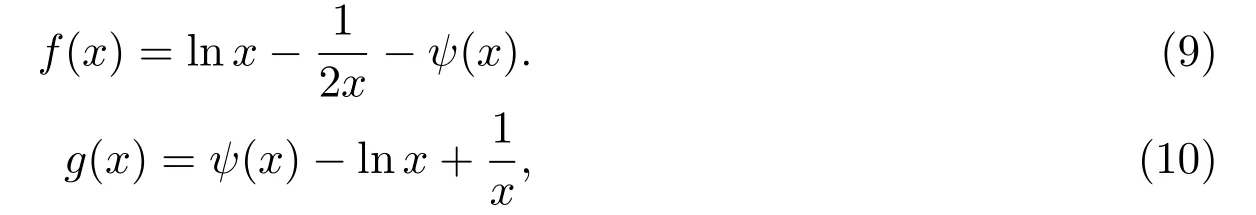
它们的q-模拟函数为:
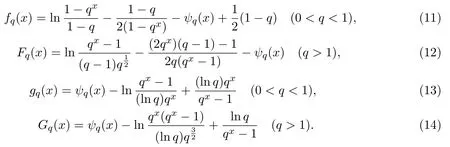
容易得到
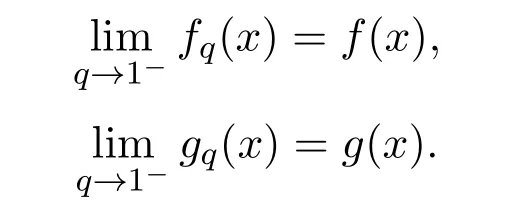
(9)式的q-模拟函数的完全单调性在文献[16-18]中被证明.近年来,研究包含psi和q-psi函数完全单调性及不等式的文献越来越多,Gamma函数、psi函数以及他们的q-模拟的许多性质和不等式在文献[19–23]中被得到.
本文主要证明了fq(x),Fq(x),gq(x),Gq(x)的完全单调性,并由它们的完全单调性得到了关于q-psi函数和q-polygamma函数的不等式.
2 引理及其证明
引理 1当x>0时,对i∈N及q∈(0,1),有
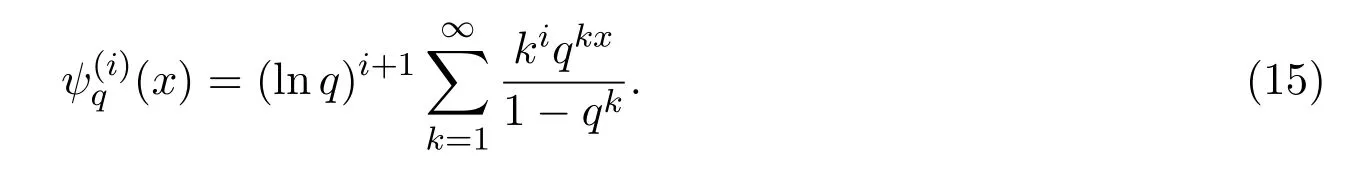
证明对(1.4)式直接求导可得到.
引理 2当x>0,q∈(0,1)时,有
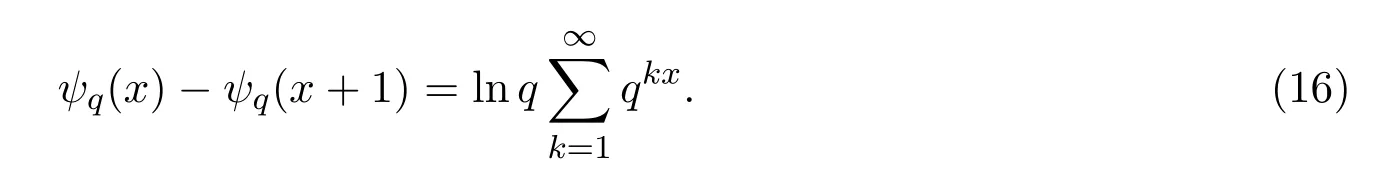
证明由(1.4)式可知,
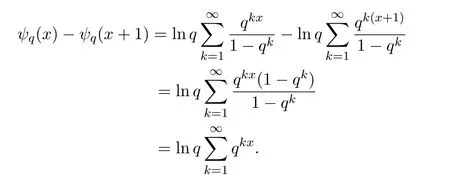
引理 3当0<p<1时,定义函数
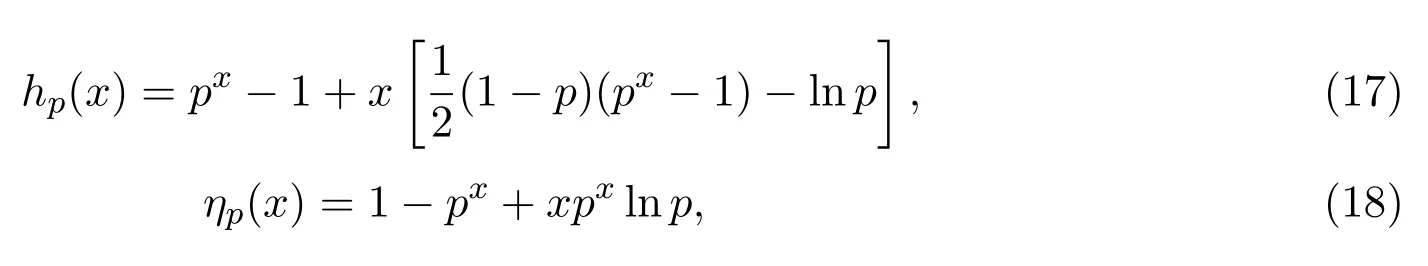
则hp(x)及ηp(x)在(0,∞)上大于零且单调递增.


引理 4 当0<q<1,对i∈N,有下面式子成立

其中fq(x)和gq(x)由(11)和(13)定义.

3 主要结论
定理 3.1当0<q<1时,(11)定义的函数fq(x)在(0,∞)上是完全单调的.


定理3.2当0<q<1时,(13)定义的函数gq(x)的二阶导数在(0,∞)上是完全单调的.

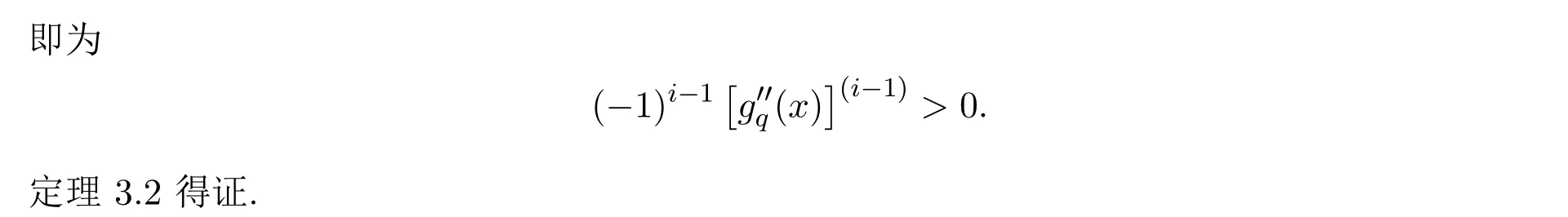
推论 3.3当q>1时,(12)定义的函数 Fq(x)及(14)定义的函数 Gq(x)的二阶导数在(0,∞)上是完全单调的.

推论 3.4当x∈(0,∞)时有下面不等式成立


[1]Gasper G,Rahman M.Basic Hypergeometric Series[M].Cambridge:Cambridge Universitty Press,1990.
[2]Alzer H.On some inequalities for the gammma and psi functions[J].Mathematises of Computation, 1997,66(217):373-389.
[3]Necdet Batir.Some new inequalities for gamma and polygamma functions[J].J.Inequal.Pure Appl.Math., 2005:6(4):103.
[4]Koornwinder T H.Jacobi functions as limit cases of q-ultraspherical polynomials[J].J.Math.Anal.Appl., 1990,148(1):44-54.
[5]Krattenthaler C,Srivastava H M.Summations for basic hypergeometric series involving a q-analogue of the digamma function[J].Computers and Mathematics with Applications.1996,32(2):73-91.
[6]Alzer H.Sharp bounds for the ratio of q-gamma function[J].Mathematische Machrichten,2001,222:5-14.
[7]Andrews G E,Askey R A,Roy R.Special Functions[M].Cambridge:Cambridge University Press,1999.
[8]Ismai M E H,Muldoon M E.Inequalities and monotonicity properties for gamma and q-gamma functions [J].Approximation and Computation.International Series of Numerical Mathematics,Birkh¨auser,Boston, MA.,1994,119:309-323.
[9]Van Haeringen H.Completely monotonic and Related Functions[J].Faculty of Technical Mathematics and Informattics,Delft University of Technology,Delft,The Netherlands,1993(3):93-108.
[10]Widder D V.The Laplace Transform[M].Princeton:Princeton University Press,1946.
[11]Day W A.On monotonicity of the relaxation functions of viscoelastic materials[J].Proc.cambridge philos.soc.,1970,67:503-508.
[12]Feller W.An Introduction to Probablity Pheory and its Applications[M].New York:Wiley,1966.
[13]Wimp J.Sequence Transformations and Their Applications[M].New York:Academic Press,1981.
[14]Qi Feng.Three classes of logarithmically completely monotonic functions involving gamma and psi functions [J].Integral Transforms Spec.Funct.,2007,18(7):503–509.
[15]Zhao JiaoLian.A completely monotonic function relating to the q-trigamma function[J].Journal of Mathematical Inequalities,2015,9(1):53-60.
[16]Chen Chaoping,Qi Feng.Logarithmically completely monotonic functions relating to the gamma function [J].Journal of Mathematical Analisis and Aplications,2006,321(1):405-411.
[17]Stamatis Koumandos.Remarks on some completely monotonic functions[J].Journal of Mathematical Aanlysis and Applications,2006,324(2):1458-1461.
[18]Qi Feng,Cui Runping,Guo Baini.Some completely monotonic functions involving polygamma functions and an application[J].Journal of Mathematical and Applications,2005,310(1):303-308.
[19]Alzer H,Grinshpan A Z.Inequalities for the gamma and q-gamma functions[J].Journal of Approximation Theory,2007,144:67-83.
[20]Batir Necdet.Some new inequalities for gamma and polygamma functions[J].J.Inequal.Pure Appl.Math.,2005,6(4):103.
[21]Gao Peng.Some monotonicity properties of gamma and q-gamma functions[J].ISRN Mathematical Analysis,2011:1-15.
[22]Ismai M E H,Lorch L,Muldoon M E.Completely monotonic functions associated with the gamma function and its q-analogues[J].J.Math.Anal.Appl.,1986,116:1-9.
[23]Tou fi k Mansour.Some inequalities for the q-gamma function[J].J.Inequal.Pure Appl.Math.,2008,9(1):18.
Complete monotonicity functions involving the q-psi function and some applications
Wang Han,Wang Liantang
(College of Mathematics,Northwest University,Xi′an 710127,China)
In this paper,the complete monotonicity for functions involving q-digamma functions are proved, some applications of these results give inequalities containing q-digamma and q-trigamma functions.
complete monotonicity,q-analogue,q-psi function,inequality,q-trigamma function
O174.6
A
1008-5513(2017)01-0082-10
10.3969/j.issn.1008-5513.2017.01.009
2016-07-13.
陕西省自然科学基金(2010JM1017).
汪韩(1992-),硕士生,研究方向:特殊函数论.
2010 MSC:26A48

