Convergence analysis of fractional iterative learning controlnonlinear systems with multiple state delays
Li Nana,Jiang Wei
(School of Mathematical Science,Anhui University,Hefei230601,China)
Convergence analysis of fractional iterative learning controlnonlinear systems with multiple state delays
Li Nana,Jiang Wei
(School of Mathematical Science,Anhui University,Hefei230601,China)
This paper presents fractional-order iterative learning control(FOILC) nonlinear system with multiple state delays.It involves external disturbances and output measurement noises which obtain some new and interesting criteria to guarantee the convergence of the tracking error in the sense of the λ-norm.The convergence of the system outputs to the desired trajectory is ensured in the absence of disturbances and output measurement noises.We estimate the upper bound of the tracking error.Finally,the validity of the proposed method are veri fi ed by an example.
fractional-order iterative learning control(FOILC),convergence, multiple time delays
1 Introduction
The formal concept of iterative learning control(ILC)was published in 1978 by Uchiyama (in Japanese)and in 1984 by Arimoto et al.Iterative learning control(ILC),which belongs to the intelligent control methodology,is an approach for improving the transient performanceof systems that operate repetitively over a fi xed time interval[1-2].In recent years,the adaptiveness and robustness of linear or nonlinear ILC schemes become very popular topics,which extended the applications of ILC to more complicated problems[4,6-7,9].Some other interesting conclusions and surveys can be found in[8,11].Moreover,in the past three years,the applications of the ILC technique to medical treatments and engineering are getting more and more popular[12-13].
优质的营商环境往往与旺盛的市场活力、富于创新的市场氛围相关联。大连营商环境短板问题主要表现在市场活力不足,激发市场活力不能靠人为干预,而在于构建健全的市场机制,让 “创新什么、怎么创新、生产什么、怎么销售”等决策真正“市场说了算”,最大程度减少行政干预和门槛限制。在众多市场作用机制中,市场导向的创新试错机制最为关键,它决定了创新的生成模式及市场活动,即依靠大众创新,并一视同仁提供公平市场竞争环境。现在的问题是过度依赖行政手段、行政指令、行政化价值观来影响市场的创新活动,不能按照市场真实需求做出正确反应和科学决策。主要有三大表现:
The FOILC is a relatively new topic in ILC,many fractional-order ILC problems were presented aiming at enhancing the performance of ILC scheme for linear or nonlinear systems [18,20].Allow for the application of fractional-order ILC scheme to the control of complex systems and the cancelation of the dependence of ILC scheme to the system orders,time delays and uncertainties are inevitable in most industrial processes.There are few research results on iterative learning control for systems with time-delay[9-10]as well as for systems with disturbance[5-6].Also robustness of the learning control is established in the presence of initial function error.However,there is little consideration on the FOILC design of nonlinear multiple time-delays system and its convergence property.
不谈收入,只谈宾利全新欧陆GT,那自然是件再惬意不过的事了。而如果将全新欧陆GT的车顶去掉,相信所收获的又会是另一片天地。我在全新欧陆GT敞篷版在上海的全球同步首发仪式现场目睹了这辆“超豪华运动旅行敞篷座驾”亮相,并试着在充斥着宾利车主的人群中,去端详它的与众不同。
关小美极力解释:“他在北京有不错的前途!可他宁愿放弃北京的高薪来到这个小城镇,这样有情有义的男人到哪里去找?”关云飞反驳说:“这正说明他做事太冲动,很不成熟。将来万一你和他处不好,你会吃大亏的……”关小美的母亲也说:“他说他是总经理他就是了啊?你也不动动脑子想想?你们认识才几天啊?”
Consider a class of fractional nonlinear multiple time-delays systems with disturbance as follows:
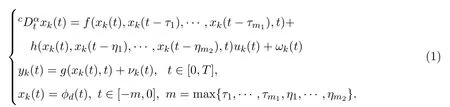
where k denotes the kth repetitive operation of the system and t is the time in the operation interval[0,T];xk(t)∈Rn,uk(t)∈Rr,and yk∈Rmare the states,control input and output of the system,respectively;wk(t)∈Rn,vk(t)∈Rmare bounded external disturbance and measurement noise;τ1,…,τm1,η1,…,ηm2are positive constant time delays;ϕd(t)is the initial piecewise continuous function of the system;Functions
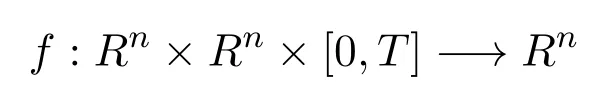
[3]Sun M X,Wang D.Sampled-data iterative learning control for nonlinear systems with arbitrary relative degree[J].Automatica,2001,37:283-289.
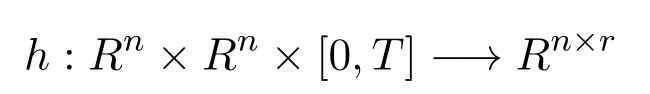
are piecewise continuous in t;g:Rn×[0,t]−→Rmis di ff erential for all x and t with partial derivatives gxand gt.
The problem on designing an ILC for uncertain plants with time delays has not been fully investigated,and only a limited number of the results are available so far.In[14],theauthor has discussed the general systems with multiple time-delays.In this paper,I take this results to FOILC.We obtain some sufficient conditions to guarantee the system outputs,states and system input to converge to desired trajectories with bounded tracking errors.When the external disturbances and measurement noises decay to zero,the bounds of the tracking errors also decay to zero.It is shown that the multiple time delays in state variables do not a ff ect the ILC convergence property signi fi cantly.
(3) 工程处治方案。由于桥隧相连部位的山体高陡,采用坡面主动防护工程规模大,且施工相当困难。故结合隧道口河流高阶地较为宽阔的有利条件,在不影响河流行洪的条件下,决定对崩塌落石影响区的桥梁调整为路基与隧道相接。这样避免了桥梁一旦受到危岩破坏而很难修复的缺点,充分发挥了路基抗灾能力相对较强的特点,并在隧道口延伸明洞,明洞上部设置必要的倾向河侧的缓冲层,进一步提高线路的抗灾能力,达到对崩塌危岩的有效处治。
2 Preliminaries
De fi nition 2.1The fractional integral of order γ with lower limit zero for a function f∈L1([0,∞))−→R can be written as
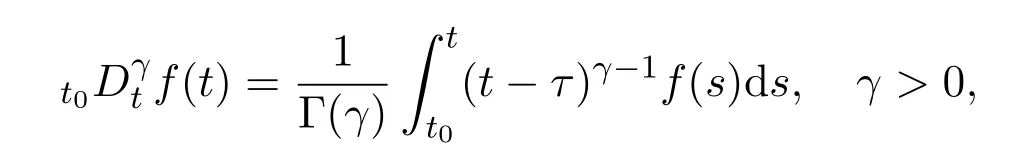
In this paper,we denote l∞norm by∥·∥,λ−norm by∥·∥λ.The following de fi nitions on norms are used in the following discussions.
De fi nition 2.2The Riemann-Liouville derivative of order γ with the lower limit zero for a function f:[0,∞)−→R can be written as
本文所有采集数据均来源于HRO观测站,大口径天线系统在B1频段增益约为78dB,采集时长为10s,数据比特位数为14,软件接收机码环阶数为2,码环相关间隔设置为0.2码片.
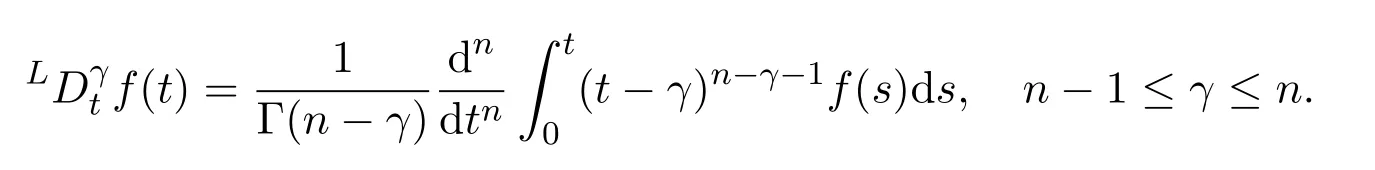
De fi nition 2.3The Caputo derivative of order γ for a function f:[0,∞)−→R can be written as
Lemma 3.1Let dibe a sequence of real number which converges to the limit d∞as i−→∞,suppose that aiis a sequence of real number such that
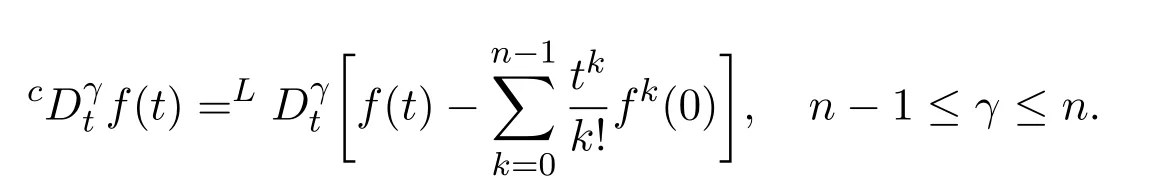
Lemma 2.4[19]Suppose β>0,m(t)is a nonnegative function locally integrable on J and n(t)is a nonnegative,nondecreasing continuous function de fi ned on n(t)≤M,t∈J,and suppose y(t)is nonnegative and locally integrable on J with
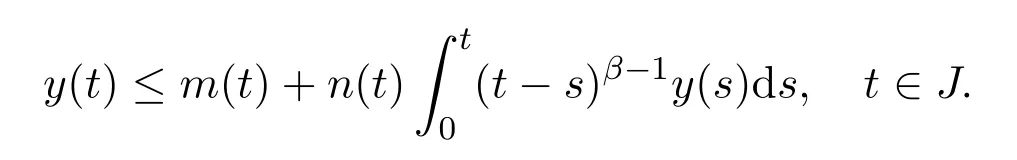
Then
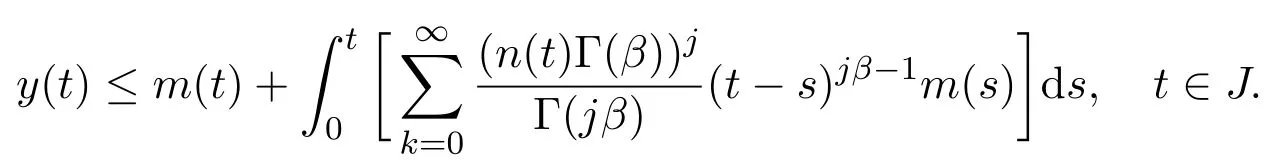
Remark 2.5Under the hypothesis of Lemma 2.4,let m(t)be a nondecreasing function on J.Then we have
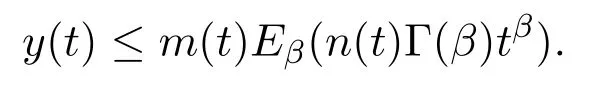
3 System respresentation and assumptions
Given a desired output bounded trajectory yd(t)and an appropriate initial condition xd(t),t∈[−m,0],there exists a unique control input ud(t),such that when uk(t)=ud(t),the system has a unique bounded desired state xd(t)satisfying:
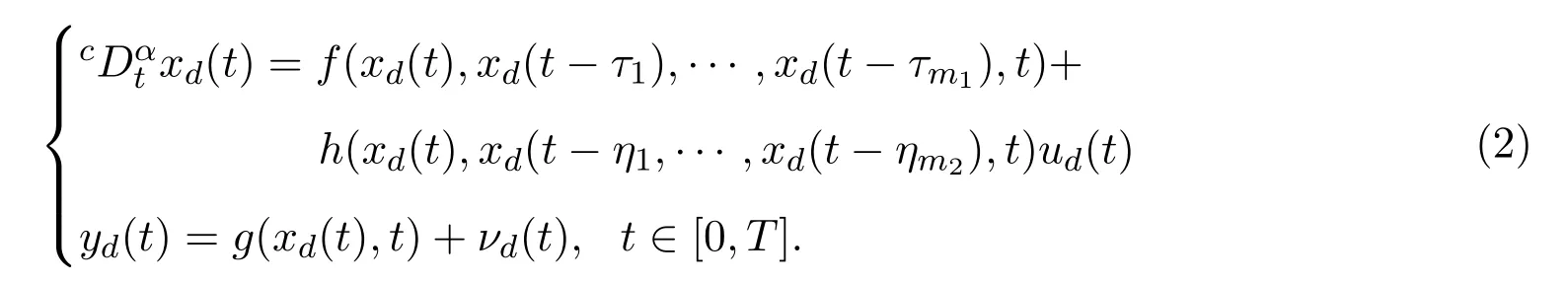
It is well known that if f and h satisfy uniformly Lipschitz conditions respectively then one can use standard methods to derive that the problem(2)has a unique solution x∈PC(J,R)(See[1])which is given by integral equation:
1.教材体系的新变化。(1)凸显教材的多功能性。由于化学课程与教学论形成了一些分支并独立成书后如果不开设选修课,就弱化了本教材的功能,造成学生认知机构的不完整。为此,把独立出去的分支教材《化学教学论实验》《化学微格教学》《化学教学测量与评价》《化学学习论》等与《化学课程与教学论》再回归为一本,发挥教材的多功能性。(2)教材体例的新变化。在每一章都设置了一些栏目。如:每一章前面用“思维导图”进行引导,使学生瞬间可浏览到一个清新直观的网络图,概览整章的知识脉络,增加对教材知识的概括性理解。
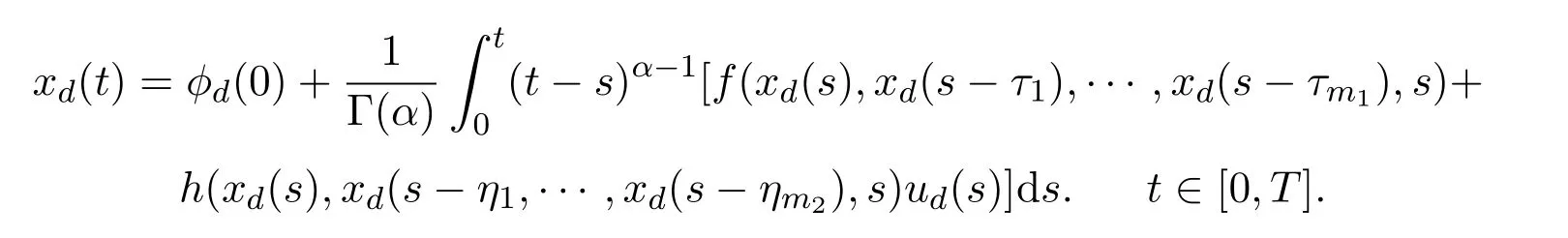
In this paper,we introduce the following assumptions:
Assumption 1The functions f,h,and gxare uniformly bounded.In the sequel,we use bf,bhand bgxto denote the upper bounds for f,h and gx.Furthermore,the input-output coupling matrix gxh is full column rank.
Assumption 2The system disturbance wk(t)and output measurement noise vk(t)are bounded by positive constants bwand bv1,respectively,on[0,T](i.e.,∥wk(t)∥≤bw,∥vk(t)∥≤bv1),andcDαtνk(t)is also bounded by positive constant bv2.
老鳜鱼一看刀子掉地上了,扑上又和我厮打,他一脸菜色,营养不良,根本没啥力气,我没费大劲,就一脚把他踢翻。他爬起来,还要跟我打,我又一脚把他踢倒。
Assumption 3The function f,g and gx,gtand h are uniformly globally Lipschitz in x on[0,T].g is di ff erentiable for all x and t with partial derivatives gxand gt.There exist positive constants kf;kh;kg;kgx;kgtsuch that:
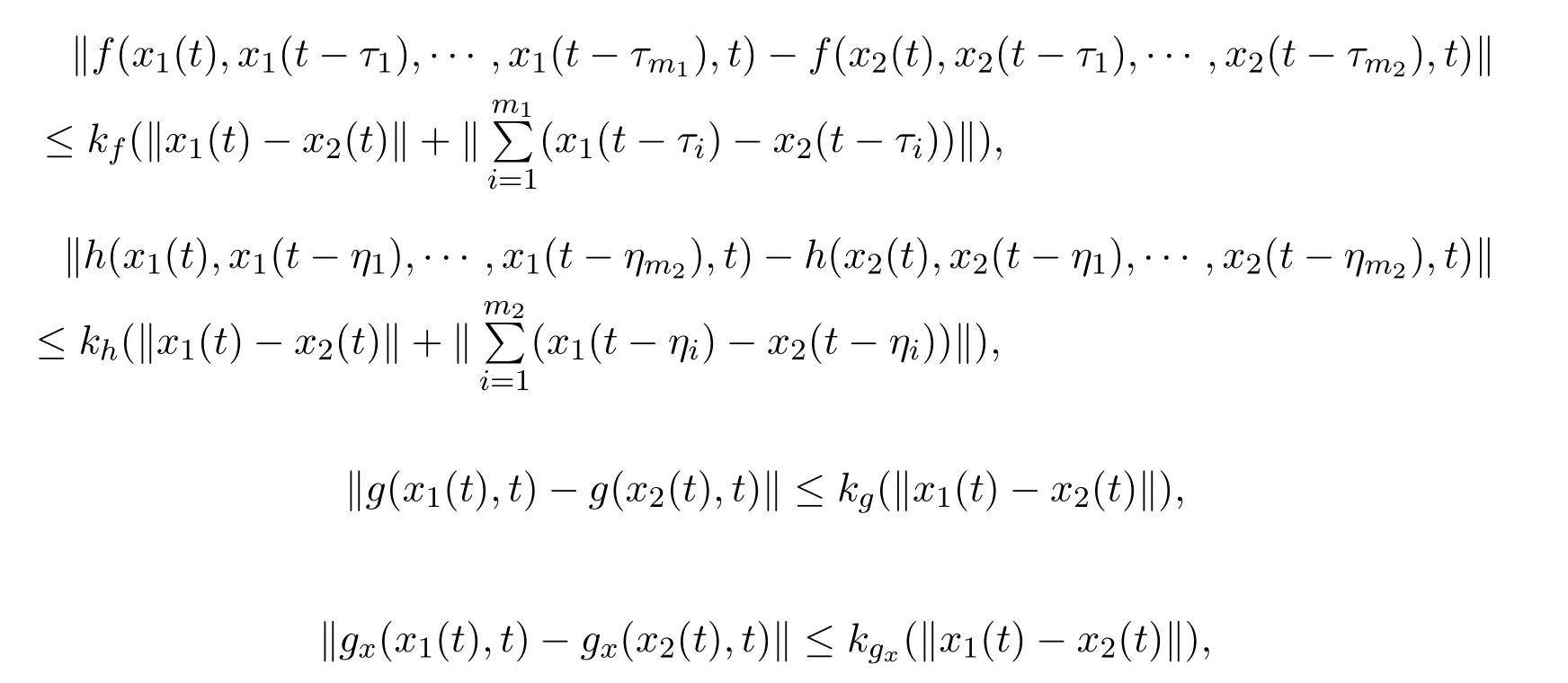
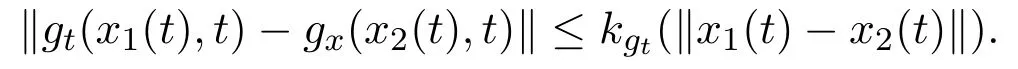
Our objective is to design an iterative scheme to generate the control input uk(t)such that the system output yk(t)converges to yd(t)and the control input uk(t)converges to ud(t)as k goes to in fi nity for all t within the time interval[0,T].
Remark 1Compared to the[14],this paper expended iterative learning control to the fractional nonlinear system with multiple time-delay.It veri fi ed that the iterative learning control and delays are irrelevant.
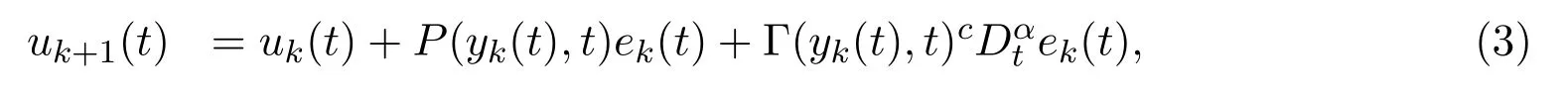
where
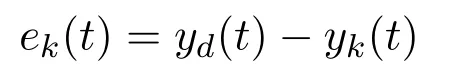
denotes the tracking error at kth repetition;P:Rm×[0,T]−→Rr×mand Γ:Rm×[0,T]−→Rr×mare learning gain matrices with norm bounds bpand bc,respectively.The control input uk(t)is piecewise continuous for all k on t∈[0,T].
For the sake of brevity,the following notations will be used:
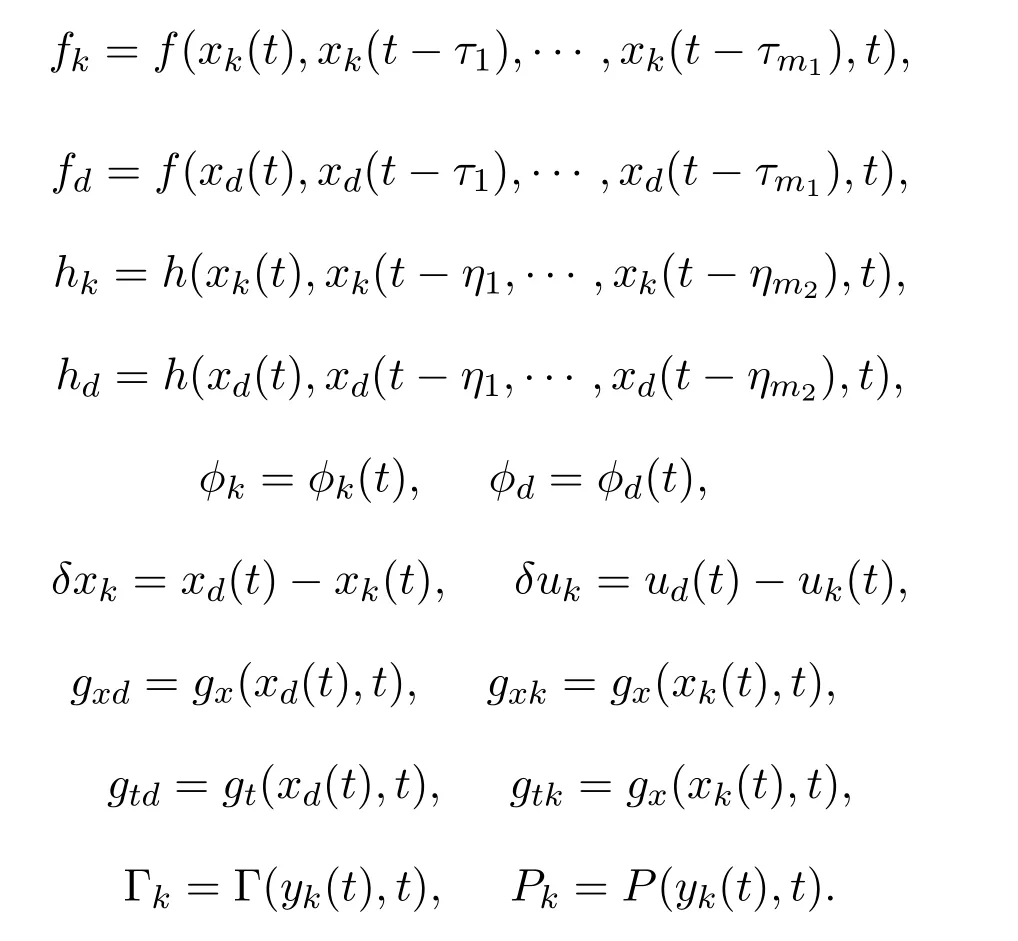
We introduce the following lemma which will be used in the following section.
试验采用随机区组设计,3次重复,小区面积50 m2。栽培密度为133 395株/hm2,株行距均为25 cm×30 cm。每小区随机抽取10株进行株高、叶片数、分蘖数的测量统计。测产时采用三点法,每小区随机抽取3个点,每个点选取1 m2进行测产。试验具体设置如表1所示。
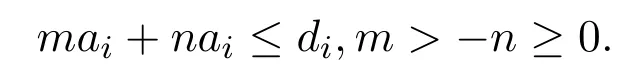
Then
魏金枝:《柔石传略》,丁景唐、瞿光熙编《左联五烈士研究资料编目》,上海文艺出版1981版,第218页。
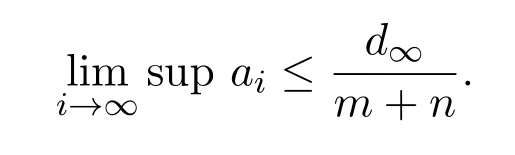
provided the right side is point-wise de fi ned on[0,∞),where Γ(·)is the gamma function.
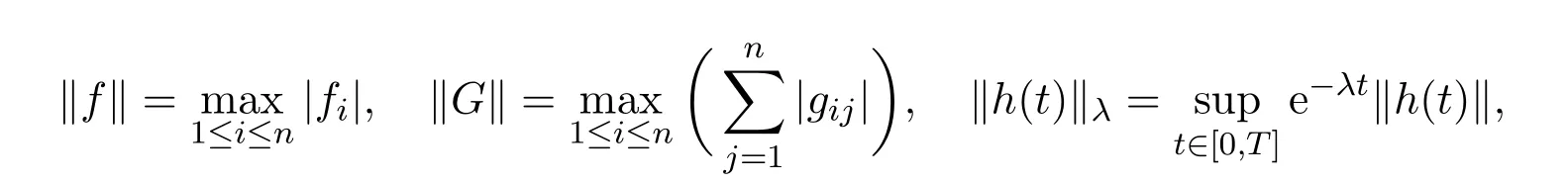
where
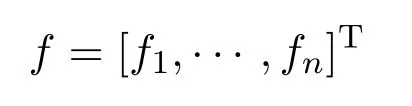
is a vector,
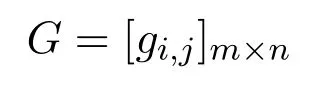
is a matrix and h(t)(t∈[0,T])is a real function.
4 Main results
(c1)∥I−Γ(,)gxk(,)h(·,·,…,·)∥≤ρ<1,and the initial condition.
Theorem 4.1Consider the fractional nonlinear multiple time-delays system(1)with ILC updating law(3)and satisfying the assumptions(1),(2),and(3).If
2.1 三组行上腹部手术患者手术时间、麻醉时间比较 三组患者手术时间、麻醉时间比较差异无统计学意义(P>0.05),见表2。
(c2)ϕk(t)=ϕd(t),t∈[−m,0]are satis fi es,and if the external disturbance and the output measurement noise approach to zero,then the bounds of the tracking error∥ud−uk∥,∥xd−xk∥, and∥yd−yk∥approach to zero when k→∞for all t∈[0,T],that is,the control input uk(t) convergences to ud(t),the state xk(t)to xd(t),and the output yk(t)to yd(t).When there exists external disturbance and measurement noise,the tracking error∥yd−yk∥is estimated as:






To realize above control objective,we consider a updating law:
(四)从世界意义看,习近平新时代中国特色社会主义思想,凝结着对人类发展重大问题的深邃思考,为解决人类面临的共同问题贡献了中国智慧。当前,世界正处于大发展大变革大调整的时期,全球治理危机频仍、挑战迭出。习近平新时代中国特色社会主义思想,顺应了“和平、发展、合作、共赢”的时代潮流,饱含了对关于人类前途命运重大问题的深邃思考,倡导构建人类命运共同体,以中国发展的实践拓展发展中国家走向现代化的途径,给世界上那些既希望加快发展又希望保持自身独立性的国家和民族提供了全新选择,为解决人类普遍面临的问题贡献了中国智慧和中国方案。
Remark 2We can observe that the bounds of the FOILC fi nal tracking errors are directly a ff ected by the disturbance and measurement noise,moreover,it can be observed that when the bounds of disturbance and measurement noise approach to zero,through the FOILC repetitive operations,the bound of tracking error∥ek(t)∥λapproaches to zero asymptotically.Therefore,iterative learning control method itself can not reject or compensate the uncertainties or disturbances for the multiple time-delay systems.
5 Numerical simulations
To demonstrate the e ff ectiveness of the proposed control scheme,the following nonlinear multiple time-delays systems with external disturbances and output measurement is presented for numerical simulations:
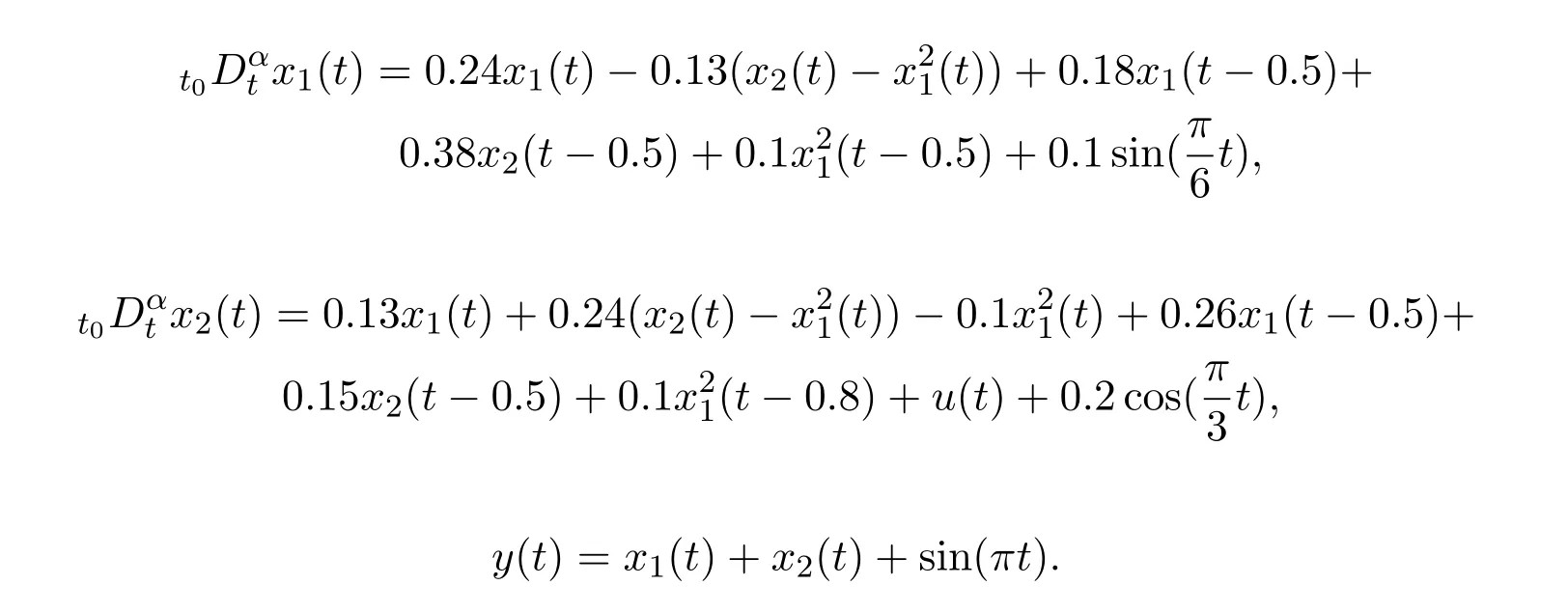
where t∈[0,2].Let us suppose that x(t)=[0.5 0.5]T;for t∈[−0.8,0]is the initial state function,and the desired trajectory is given by yd(t)=1.The objective of the control is to track the trajectory yd(t),over the time interval t∈[0,2].The simple choices of the control gains P and Γ in iterative learning control rule(3)are P=Γ=0.1.We apply the proposed FOILC rule(3)to the nonlinear system.By calculation,we can show the tracking performance of the FOILC system output at the interval t∈[0,2]when the FOILC rule(3)is iterativelyexecuted at di ff erent times.If the tolerance bound is chosen to be equal to 0.015,we fi nd that the control objective is achieved at the 11th iteration.Our simulation results illustrate that the proposed ILC rule in the form of(3)is robust with respect to small disturbance and measurement noises.
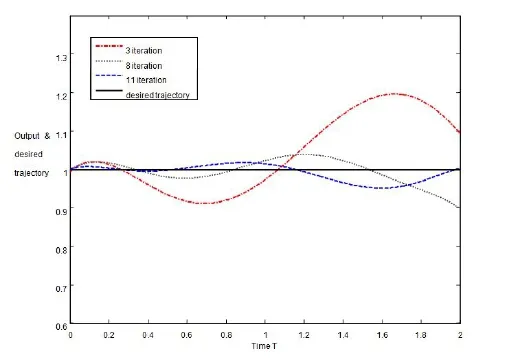
Fig.1 The solid line represents the desired trajectory yd(t),and the dashed,the dotted, and the dashed-dotted lines represent the FOILC system output yk(t)when the FOILC rule has executed 3,8,11 times,respectively.
[1]Podlubny I.Fractional Di ff erential Equations[M].New York:Academie Press,1999.
[2]Hilfer R.Application of Fractional Calculus in Physics[M].Singapore:World Science Publishing,2000.
首先对社会隔离、生存质量和经济状况进行描述性分析和Pearson相关分析。如表1所示。社会隔离均值为(1.578±0.598)分,生存质量、经济状况均值分别为(3.894±0.514)分和(2.270±0.599)分。社会隔离与生存质量(r=-0.222,P<0.01)呈显著负向相关性,与经济状况(r=-0.090,P<0.05)呈显著负向相关性。生存质量和经济状况呈显著正向相关性(r=0.183,P<0.01)。
and
[4]Xu J X.A new fuzzy logic learning control scheme for repetitive trajectory tracking problems[J].Fuzzy Sets and Systems,2003,133:57-75.
[5]Park K H,Bien Z H,Wang D H.Design of an iterative learning controller for a class of linear dynamic systems with time delay[J].IEE Proceedings Control Theory and Applications,1998,145:507-512.
[6]Zhang B L,Tang G Y,Zhen S.PD-type iterative learning control for nonlinear time-delay system with external disturbance[J].Journal of Systems Engineering and Electronics,2006,44:600-605.
[7]Li Y,Chen Y Q,Ahn H S.Fractional-order iterative learning control for fractional-order linear systems[J].Asian Journal of Control,2011,13:1-10.
其中,Ndeep(l,x)为搜索深度,其定义如式(4)所示,且1≤ Ndeep(l,x) ≤Nr;C为更新半径,且C2=2Nr σ2,为常数.Rx-SD检测依靠式(3)来更新搜索半径,减小了接收端的搜索范围,降低了接收端的计算复杂度.
[8]Chen Y Q,Wen C Y.Iterative Learning Control)Convergence,Robustness and Applications[C].London: Springer,1999.
[9]Lan Y H,He L J.P-type iterative learning control of fractional order nonlinear time-delay systems[J].In: Proceedings of the 24th Chinese Control and Decision Conference,2012:1027-1031.
[10]Sun M X,Wang D.Initial condition issues on iterative learning control for nonlinear systems with time delay[J].International Journal of Systems Science,2001,32:1365-1375.
[11]Benchohra M,Henderson J,Ntouyas S K,et al.Existence results for fractional order functional di ff erential equations with in fi nite delay[J].Journal of Mathematical Analysis and Applications,2008,338:1340-1350.
[12]Li Y,Chen Y Q,Ahn H S.Fractional-order iterative learning control for fractional-order linear systems[C].In Proceedings of the Symposium on Learning Control at IEEE CDC 2009.China:Shanghai,2009.
[13]Deng W H.Smoothness and stability of the solutions for nonlinear fractional di ff erential equations[J].Nonlinear Anal.,2010,72:1768-1777.
[14]Ma F,Li C.Iterative learning control design of nonlinear multiple time-delay systems[J].Applied Mathematics and Computation,2011,218:4333-4340.
[15]Geng X G,Xue B.An extension of integrable peakon equations with cubic nonlinearity[J].Nonlinearity, 2009,22:1847-1856.
[16]Lazarevic M P.PDα-type iterative learning control for fractional LTI system[C].Proceedings of the 16th International Congress of Chemical and Process Engineering.2004:1503-1507.
[17]Kilbas A A,Srivastava H M,Trujillo J J.Theory and Applications of Fractional Di ff erential Equations[J].Amsterdam:Elsevier,2006.
[18]Bristow D A,Tharayil M,Alleyne A G.A survey of iterative learning control[J].IEEE Control Systems Magazine,2006,26:96-114.
[19]Jiang W.The controllability of fractional control systems with control delay[J].Computers and Mathematics with Applications,2012,64:3153-3159.
[20]Ye H,Gao J,Ding Y.A generalized Gronwall inequality and its application to a fractional di ff erential equation[J].Journal of Mathematical Analysis and Applications,2007,328:1075-1081.
含多重时滞非线性系统的分数阶迭代学习控制的收敛性分析
李娜娜,蒋威
(安徽大学数学科学学院,安徽,合肥 230601)
本文研究了含多重时滞非线性系统的分数阶迭代学习控制(FOILC).它包含了外部干扰和输出控制噪音,通过引入λ-范数,获得在开环和闭环迭代学习控制作用下,系统控制输入以及跟踪误差收敛的充分条件.最后,通过数值仿真验证所提方法的有效性.
分数阶迭代学习控制,收敛,多重时滞
O231.2
2016-10-10.
国家自然科学基金(11371027,11471015).
李娜娜(1990-),硕士生,研究方向:泛函微分方程理论方向.
A
1008-5513(2017)01-0069-13
10.3969/j.issn.1008-5513.2017.01.008
2010 MSC:93C15,93C40,34A37

