一类几何流方程周期解的爆破
汪瑶瑶
(安徽师范大学计算机科学学院,安徽 芜湖 241003)
一类几何流方程周期解的爆破
汪瑶瑶
(安徽师范大学计算机科学学院,安徽 芜湖 241003)
研究双曲平均曲率流中一类几何流方程周期解的爆破问题.引入合适的黎曼不变量,将该方程化为对角型的一阶拟线性双曲型方程组.该方程组在Lax意义下不是真正非线性的.假设初值是周期的,且在一个周期内全变差很小,此外假设初值还满足一定的结构条件,可以证得该几何流方程的周期解必在有限时间内发生爆破,解的生命跨度估计可以给出.
几何流方程;拟线性双曲型方程组;周期解;爆破;生命跨度
1 引言
平均曲率流是一类非线性偏微分方程组,用以研究曲面或流形随时间的演化,其特征是速度向量等于流形法向向量乘以某个几何量,这个几何量可以是曲率、平均曲率和逆平均曲率等.平均曲率流已被用来成功解决若干几何和拓扑问题,例如文献[1]提出的逆平均曲率流,成功证明了黎曼流形中的Penrose不等式.而近年来,对于双曲型几何流的研究越来越得到重视,做了不少工作.
2009年,文献[2]提出如下的双曲平均曲率流:
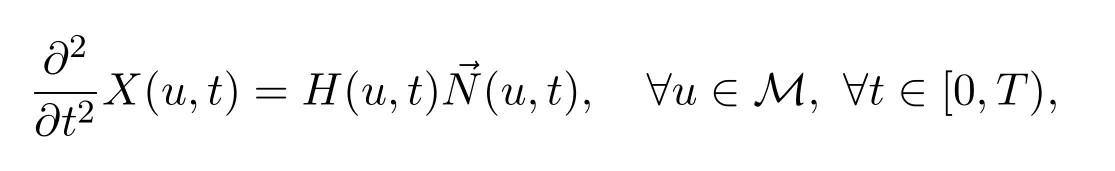
这里M是黎曼流形,X(·,t):M→ℝ1+n是光滑映射,H(u,t)是平均曲率,(u,t)表示外法向量,T是一个正常数.上述方程组是二阶的非严格双曲型偏微分方程.运用一些分析的技巧,文献[1-2]将方程组化为严格双曲型的,进而得到解的局部存在唯一性,维数大于4的欧式空间的非线性稳定性也得到证明.此外,文献[1]给出了曲率所满足的非线性波动方程.文献[3]通过包含动能和内能的泛函导出一类如下的非线性几何发展方程,

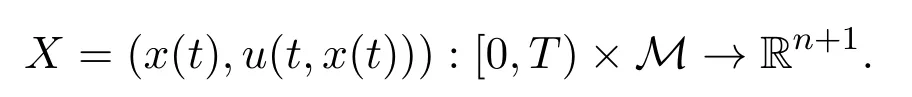
特别地,对于一维情形,文献[3]推导出如下的方程:
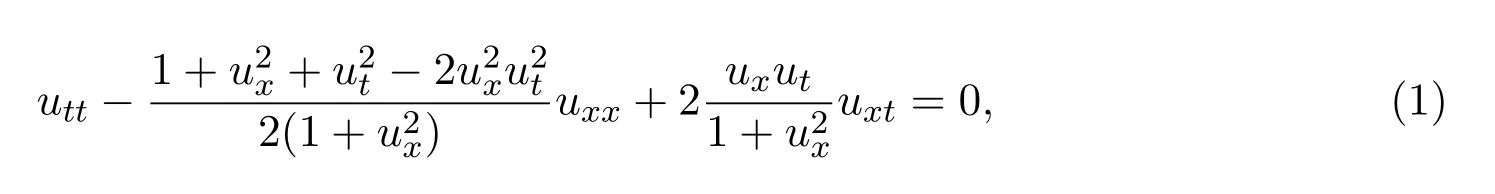
设初值为:
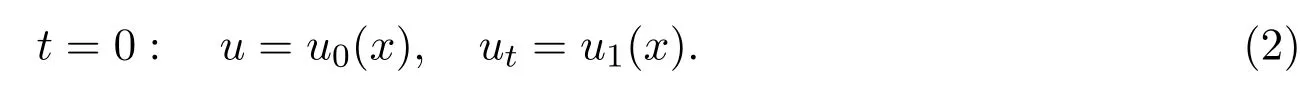
初值问题(1)和(2)可用来刻画无穷长弦的振动,上述u0(x),u1(x)分别表示弦的初始位置和初始速度.文献[3]证明了当初值的BV模小时,初值问题(1)和(2)的熵弱解是整体存在的.2011年,文献[5]考虑如下关于凸超曲面的双曲曲率流:

其中 F被称为drving force,bij是一致凸超曲面第二基本形式的逆.文献[5]指出,选择不同的F,可以导致不同非线性双曲型方程,例如可以导出双曲型的Monge-Amp`ere方程.此外,文献[5]证明了对于一大类F,方程组(3)的局部可解性,并考虑了解的爆破性质以及解的渐近行为等.
2009年,文献[4]研究了对于平面曲线的双曲平均曲率流,即如下偏微分方程组的初值问题:
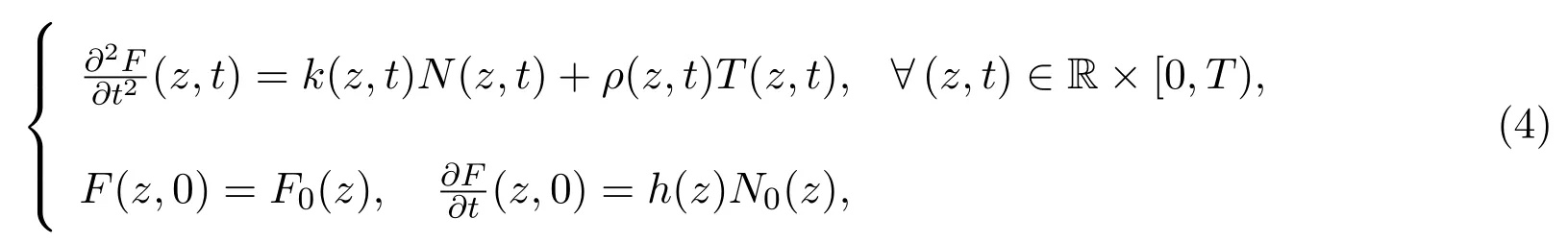
其中F(z,t)表示未知量,k(z,t)是曲线F(z,t)的平均曲率,N(z,t)表示单位法向量,T(z,t)是单位切向量,F0(z)表示初始曲线,而h(z)和N0(z)分别代表初始速度大小和初始曲线的法向量;函数 ρ(z,t)由下式定义,
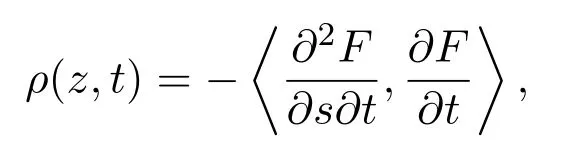
这里s是弧长参数.文献[4]得到了初值问题(4)的局部适定性,特别地,他们研究了以图形式存在的曲线F(x,t)=(x,u(x,t))的周期运动.由于相应的双曲型方程组在Lax意义下不是真正非线性的,周期解的讨论并不简单.通过引入黎曼不变量,上述方程组可化为对角型双曲型方程组.文献[4]通过详细研究两族特征的相互作用,得到在初值具有小变差以及满足一定的结构条件时,平均曲率流方程组的周期解会发生爆破,且给出了解生命区间的估计.此同时,文献[6]研究在双曲平均曲率流(4)下平面闭曲线的运动.考虑将曲线支撑函数作为未知量,得到一类双曲型的Monge-Amp`ere方程.基于此,Kong、Liu和Wang证明了相应初值问题的经典解仅仅在区间[0,Tmax)存在,且当t→Tmax时,解收敛到一点或者激波或者其他间断解.文献[4]在此基础上,考虑了Minkowski时空中的平均曲率流方程组和可化约的一阶双曲型方程组的周期初值问题,并得到解的生命跨度.
本文研究上述几何流方程组(1)和(2)的周期解问题.对于双曲型方程组的周期解问题,目前也已经有了很多的研究.文献[9]利用黎曼不变量研究2×2双曲型方程组的周期解和奇性形成,并讨论了解的大时间衰减刻画.文献[10]研究了非线性振动弦初值为周期的柯西问题的爆破,解的生命跨度依赖于平衡态附近的非线性效应.文献[8]将他们的结果推广到一般的可化约的一阶双曲型方程组.文献[7]研究了双曲型微分方程周期解的存在问题.文献[13]研究了2×2的拟线性双曲方程组的周期解的爆破问题,爆破的产生也是源于同族特征线的相交.文献[15]将Glimm、Lax的结果推广到3×3的双曲型方程组,考虑非等熵Euler方程组的周期初值问题.通过选取合适的黎曼不变量和推广的Glimm泛函,他们得到了当初值具有小变差ε时,初值问题熵解的生命跨度是O(ε−2).文献[18]也研究了一类非等熵Euler方程组的周期初值问题,所用方法是基于文献[13].
本文结构如下:第2节给出本文的主要结果,同时给出一些准备工作;第3节将证明一些重要的引理;第4节给出定理的证明.
2 主要结果
在给出本文主要结果之前,我们先做些准备工作.


命题 2.1方程组(6)是严格双曲型方程组,具有两个互异的特征值(8),右特征向量可取为(9)式;同时,由(10)式可知,方程组(6)在Lax意义下不是真正非线性的.


下面是本文主要结果.
定理 2.1给定 R0(x),S0(x)是 C1光滑函数,如果 R0(x),S0(x)满足 (21)-(22),且假设(23)式或者(24)式成立,那么初值问题(19)-(20)的C1解在有限时间内将发生爆破,解的生命跨度T(δ)满足

现在考虑初值问题(1)和(2)的周期解问题.设初值u0(x),u1(x)是C1的光滑函数,且满足:
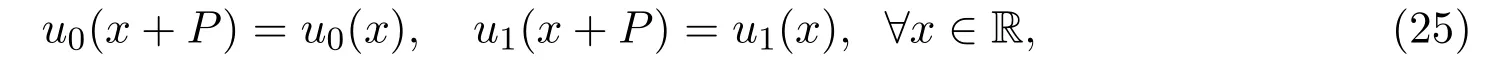
这里P是非负常数.由定理2.1可得如下结果.
定理 2.2由上述讨论,可取
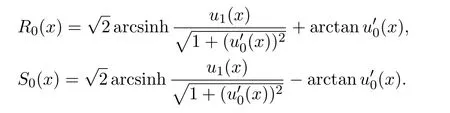
则R0(x),S0(x)是C1光滑的以P为周期的函数.此外,假设(23)式或者(24)式成立,则初值问题(1)和(2)的C1解在有限时间内发生爆破,且解的生命跨度T(δ)满足
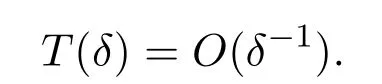
3 若干引理
本节我们做些准备工作,引入若干引理,为定理2.1的证明作铺垫.
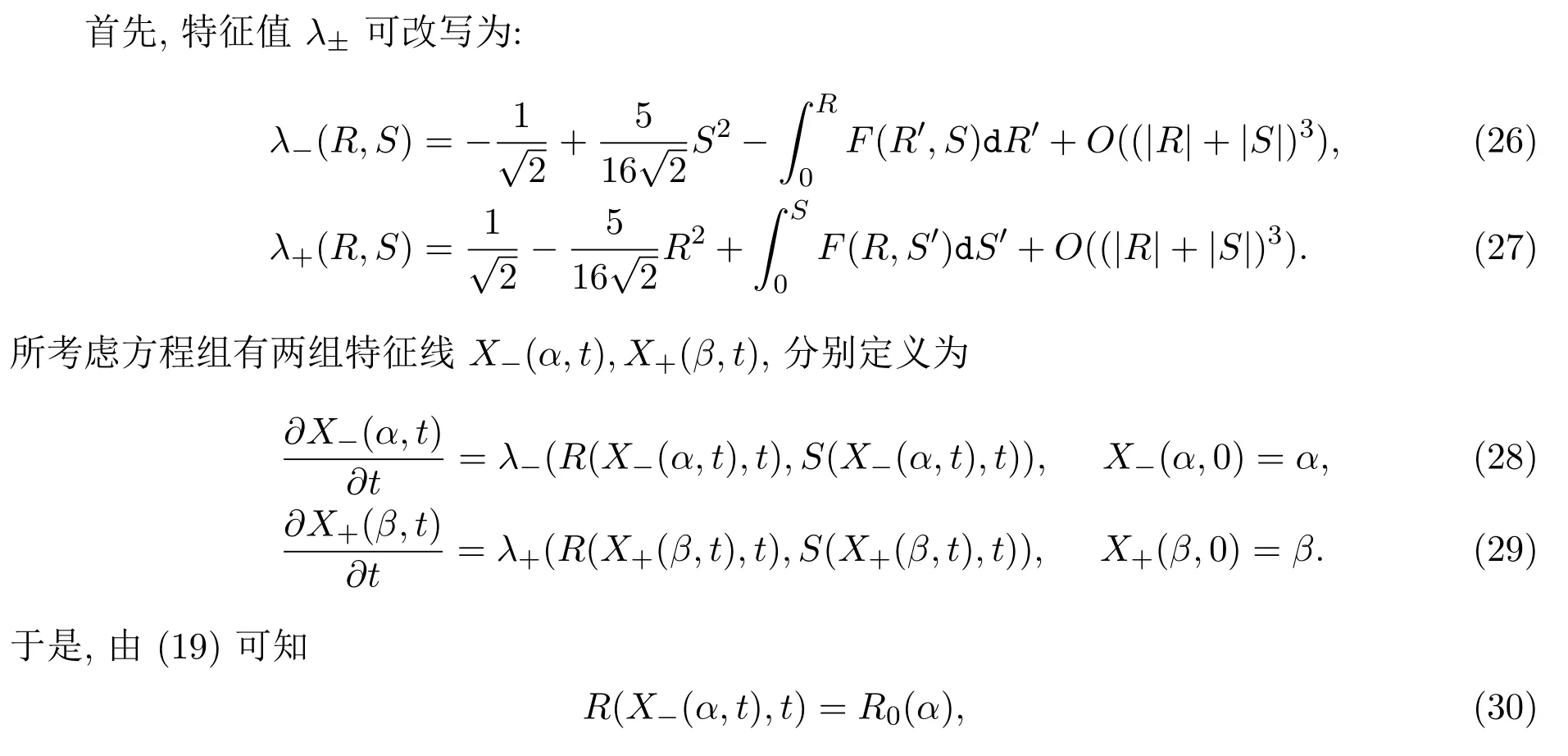


下面给出若干引理,它们将在后面证明和讨论中起重要作用.
引理 3.1定义

证明证明可参见文献[4],此处从略.
引理 3.2在初值问题(19)和(20)C1解的存在范围内,始终成立
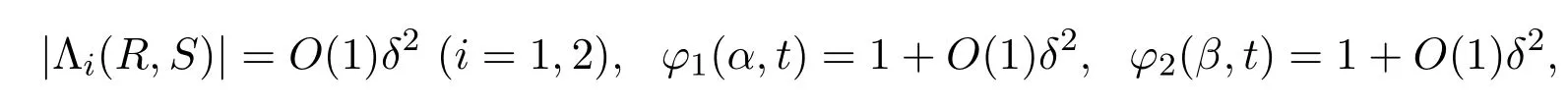
这里及以后,记号O(1)均表示有界量.

引理 3.3给定α,∀β≤α,定义t1(β;α)使得
另一方面,本文测量系统还采用了WeBee公司的B-0004蓝牙模块实现无线通信功能[18],其原理图如图9所示。从图可以看出,蓝牙芯片只需要RXD和TXD两个引脚与单片机相连即可以工作,占用的单片机资源很少,使用起来很方便。
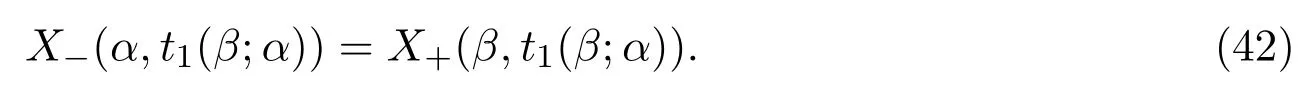
给定β,∀α≥β,定义t2(α;β)使得

则
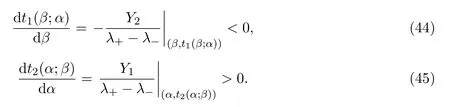
证明证明方法类似于文献[4],此处省略.
引理 3.4(i)成立如下估计式:

(ii)(a)若 β2≤β1≤α,则
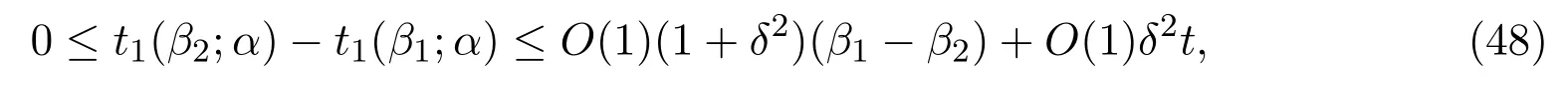
(b)若β≤α1≤α2,则

(iii)对Y1和Y2有
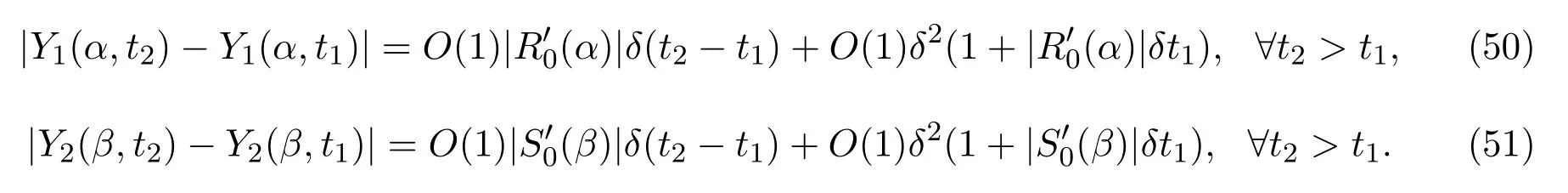


引理 3.5成立如下估计:
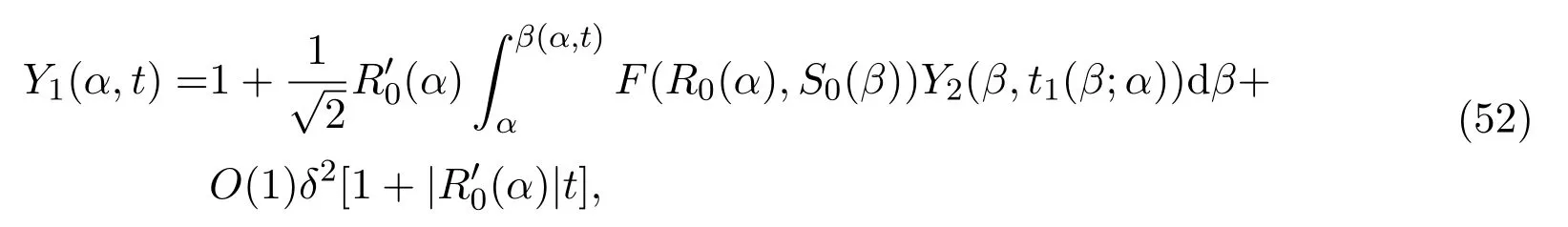
和
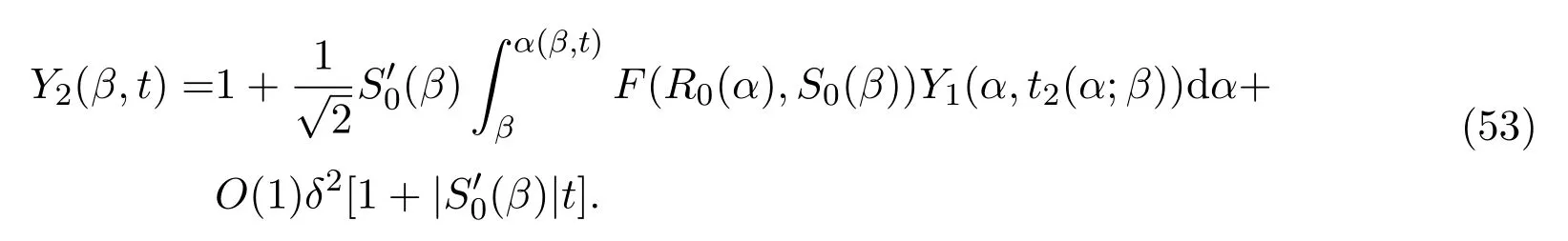

即我们已经证明了(52).类似地,可证得(53).
引理 3.6假设成立如下不等式


4 定理的证明


[1]He C L,Kong D X,Liu K F.Hyperbolic mean curvature fl ow[J].Di ff erential Equations,2009,246:373-390.
[2]Huisken G,Ilmanen T.The inverse mean curvature fl ow and the Riemannian Penrose inequality[J].Di ff erential Geom.,2001,59:353-437.
[3]Le fl och P G,Smoczyk K.The hyperbolic mean curvature fl ow[J].Math.Pures.Appl.,2008,90:591-614.
[4]Kong D X,Wang Z G.Formation of singularities in the motion of plane curves under hyperbolic mean curvature fl ow[J].Di ff erential Equations,2009,247:1694-1719.
[5]Chou K S,Wo W F.On hyperbolic Gauss curvature fl ows[J].Di ff erential Geometry,2011,89:455-485.
[6]Kong D X,Liu K F,Wang Z G.Hyperbolic mean curvature fl ow:Evolution of plane curves[J].Acta Math.Sci.,2009,29:493-514.
[7]Cesan Lamberto.Existence in the large of periodic solutions of hyperbolic partial di ff erential equations[J].Archive for Rational Mechanics and Analysis,1965,20:170-190.
[8]Cheng K S.Formation of singularities for nonlinear hyperbolic partial di ff erential equation[J].Contemp.Math.,1983,17:45-56.
[9]Glimm J,Lax P D.Decay of solutions of systems of nonlinear hyperbolic conservation laws[J].Mem.Am.Math.Soc.,1970,101:1-112.
[10]Klainerman S,Majda A.Formation of singularities for wave equations including the nonlinear vibrating string[J],Comm.Pure Appl.Math.,1980,33:241-263.
[11]Kong D X,Wang Z G.Formation of singularities in the motion of plane curves under hyperbolic mean curvature fl ow[J].Di ff erential Equations,2009,247:1694-1719.
[12]Li T T.Global Classical Solutions for Quasilinear Hyperbolic Systems[M].Paris:Wiley-Masson,1994.
[13]Li T T,Kong D X.Blow up of periodic solutions to quasilinear hyperbolic systems[J].Nonlinear Anal., 1996,26:1779-1789.
[14]Lax P D.Hyperbolic systems of conservation laws II[J].Comm.Pure Appl.Math.,1957,10:537-556.
[15]Qu P,Xin Z P.Long time existence of entropy solutions to the one-dimensional non-isentropic Euler equations with periodic initial data[J].Arch.Rational Mech.Anal.,2015,216:221-259.
[16]Wang Z G.Hyperbolic mean curvature fl ow in Minkowski space[J].Nonlinear Analysis,2014,94:259-271.
[17]Wang Z G.Blow-up of periodic solutions to reducible quasilinear hyperbolic systems[J].Nonlinear Analysis, 2010,73:704-712.
[18]Xiao J J.Some topics on hyperbolic conservation laws[D].Hong Kong:The Chinese University of Hong Kong,2008.
Blowup of periodic solutions for nonlinear equations of geometric fl ow
Wang Yaoyao
(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China)
This article considers the blow up problem for a class of nonlinear partial di ff erential equations of geometric fl ow.By introducing the proper Riemann invariants,the equations can be reduced into a system of quasilinear hyperbolic equations in the diagonal form,which are not genuinely nonlinear in the sense of Lax.Under the assumptions that the initial data have small total variations in one period and some certain conditions are satis fi ed,the C1solutions can be proved to blow up in fi nite time.In addition,the life span of the C1classical solutions are derived.
PDE of geometric fl ow,quasilinear hyperbolic equation,periodic solution,blow up,life span
O175.2
A
1008-5513(2017)01-0044-16
10.3969/j.issn.1008-5513.2017.01.006
2016-10-11.
国家自然科学基金(11301006);安徽省自然科学基金(1408085MA01).
汪瑶瑶(1990-),硕士,研究方向:偏微分方程.
2010 MSC:35L60,35L45

