一类三元反向混合单调算子不动点定理及其应用

谢卢梦,薛西锋

(西北大学数学学院,陕西 西安 710127)

一类三元反向混合单调算子不动点定理及其应用

谢卢梦,薛西锋

(西北大学数学学院,陕西 西安 710127)

利用单调迭代方法、数学归纳法、锥理论方法研究了具有半序的Banach空间反向混合单调算子的不动点的存在性与唯一性,得到的结论推广了反向混合单调算子不动点的存在性与唯一性.最后,将所得到的结论应用于Hammerstein积分方程中.

反向混合单调算子;正规锥;不动点;迭代序列

1 引言

在具有半序的 Banach空间中,混合单调算 子[1]和反向混合单调算 子[2]理论在方程求解方面有相当广泛的应用.文 献[3]研究了在序差关系下的反向混合不动点存在性与唯一性,文献[4]引进了混合g-单调的概念并研究了混合g-单调算子的耦合不动点的存在性与唯一性,文献[5]将混合g-单调算子下的不动点存在性与唯一性做了推广,文献[6]在非紧性与非连续性以及u0-凹凸性的条件下给出了一种新的混合单调算子的不动点定理,文献[7]对其结论做了推广.受到上面学者所研究的文献的启发,本文在假设算子不具有紧性与连续性这一条件下,得到在具有半序Banach空间中的一类新的三元反向混合单调算子的不动点的存在性与唯一性.

2 预备知识

设 E是实 Banach空间,P⊂E是一个锥.若对任意的 x,y∈P,x≤y 当且仅当有 y−x∈P时,称半序关系≤ 是由 P导出的.如果存在常数 N ＞0,使得对任意的x,y∈P,θ≤x≤y,都有||x||≤N||y||成立,称锥P为正规锥,其中N 为正规常数.

设E是半序线性空间,令

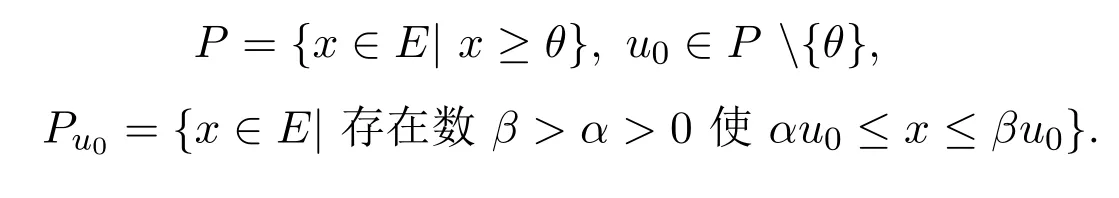
定义 2.1[9]设E是具有半序关系的Banach空间,定义乘积空间E×E×E中的半序关系:如果

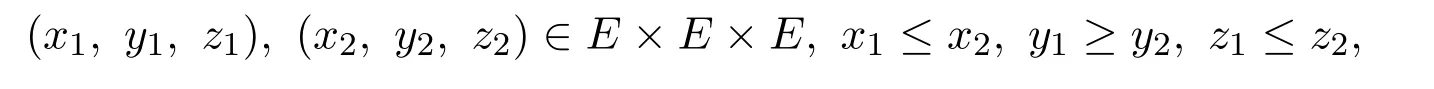
则记(x1,y1,z1)≤(x2,y2,z2).

定义 2.2设A:E×E×E→E,若x1≤x2,y1≥y2,z1≤z2,蕴含着

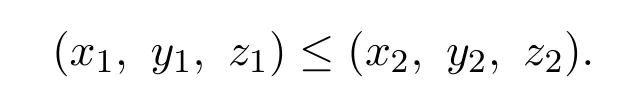
则称A为反向混合单调算子.即对任意的x,y,z∈E有下列结论:

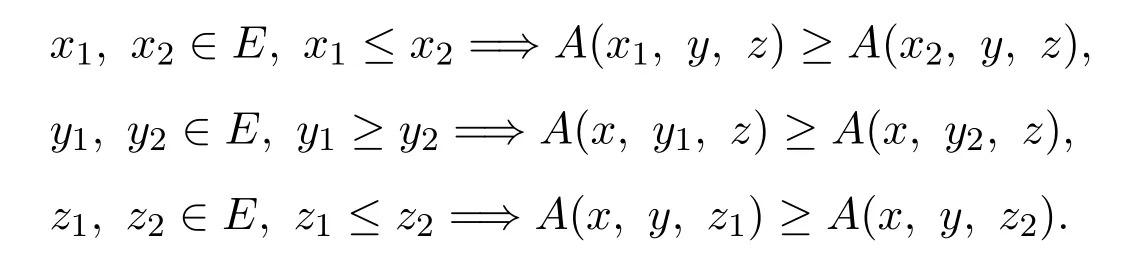
定义2.3[9]设x∈E,A:E×E×E→E,若x=(x,x,x),则称x为A的三重不动点.

3 主要结论

定义 3.1设A:P×P×P→P,u0∈P{θ},η:(R×P×P×P)→R.如果

(i)对任给的x,y,z∈P{θ},A(x,y,z)∈Pu0;

(ii)对任给的x,y,z∈Pu0,t∈(0,1),存在η(t,x,y,z)≥0,使得

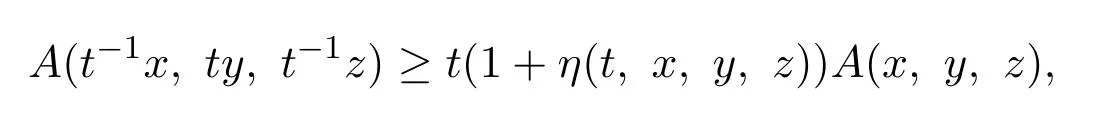
则称A:P×P×P→P的一个u0-凹凸算子.其中η(t,x,y,z),对固定的y,z关于x是减的,对固定的x,y关于z是减的,对固定的x,z关于y是增的.

定理3.1设P是E中的正规锥,令A:P×P×P→P是一个反向混合单调u0-凹凸算子.假设x0,y0,z0∈P且x0≤y0,z0≤y0.满足下列条件:

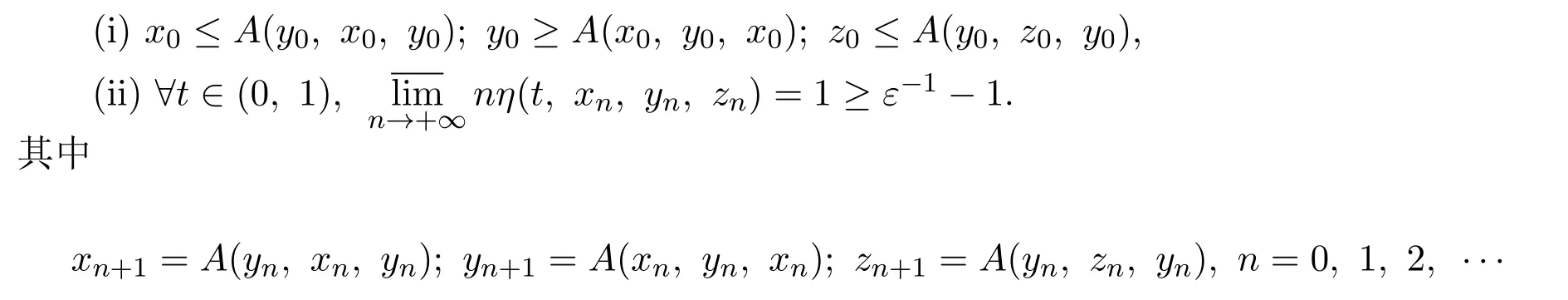
证明条件(i),(iii)满足定理3.1中的条件(i),(ii).则由定理3.1可知该命题成立.

定理 3.2设P是Banach空间E中的正规锥,令算子A是一个反向混合单调u0-凹凸算子.假设 x0,y0,z0∈P 且 x0≤ y0,z0≤ y0,∀t∈(0,1),其中 η(t,x,y,z)如定义 3.1所述,则算子 A在 P上有唯一的不动点的充分必要条件是定理3.1中的条件(i)成立.以x0,y0,z0为初始值作迭代序列:

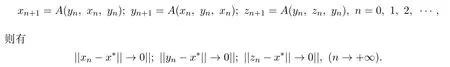
4 应用

下面给出定理3.1在Hammerstein积分方程中的应用.

设

考虑积分方程

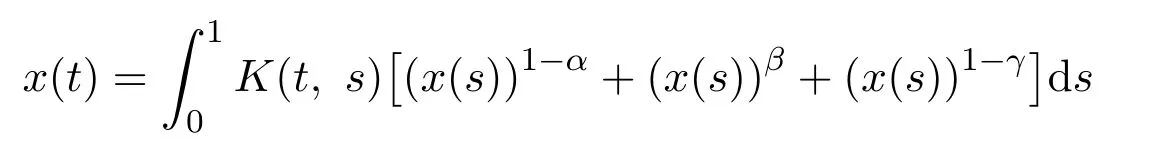
其中α,β,γ∈(0,1)为常数.

定理 4.1设K:[0,1]×[0,1]→(0,+∞),∀t∈(0,1),假设存在

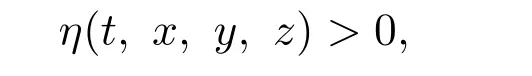
参考文献

[1]Guo Dajun,Lakskmikantham V.Coupled fi xed point of mixed monotone operator with application[J].Nonlinear Analysis,1987,11:623-632.

[2]孙义静.一类非线性算子方程组的迭代算法及应用[J].浙江大学学报:自然科学版,1999,3:289-294.

[3]王维娜,薛西锋.混合单调算子对的新不动点定理及应用[J].纺织高校基础科学学报,2014,9:328-331.

[4]Lakshmikantham V,Ciric L.Coupled fi xed point theorems for nonlinear contractions in partially ordered metric spaces[J].Nonlinear Anal.,2009,70:4341-4349.

[5]Marin Borcut.Tripled coincidence theorems for contractive type mappings in partially ordered metric spaces[J].Applied Mathematics and Computation,2012,218:7339-7346.

[6]Xinsheng Du.New fi xed point theorems of mixed monotone operators[J].Applied Mathematics,2014,5:352-357.

[7]Hojjat Afshari.New tripled fxied point theorems of mixed monotone operators and applicaions[J].Journal of Nanjing University Mathematical Biquarterly,2014,10:174-186.

[8]孙经先.非线性泛函分析及其应用[M].北京：科学出版社,2007.

[9]Vasile Berinde,Marin Borcut.Tripled fi xed point theorems for contractive type mappings in partially ordered metric spaces[J].Nonlinear Analysis,2011,74:4889-4897.

Fixed point theorems of a type tripled reverse mixed monotone operator

Xie Lumeng,Xue Xifeng
(Department of Mathematics,Northwest University,Xi′an 710127,China)

In order to explore the existence and uniqueness of triple fi xed point of reverse mixed monotone operator which in partially ordered Banach space,the mixed monotone iterative method and mathematical induction and cone theory are used.The results generalize the existence and uniqueness of fi xed point of reverse mixed monotone operator.

reverse mixed monotone operator,normal cone, fi xed point,iteration sequence

O178

A

1008-5513(2017)01-0060-09

10.3969/j.issn.1008-5513.2017.01.007

2016-05-23.

陕西省自然科学基金(2012JM1017).

谢卢梦(1991-),研士生,研究方向：非线性泛函分析.

2010 MSC:47H10