DAS组合密封圈密封特性
夏毅敏,张欢,罗春雷,金耀,曾雷,禹宏云
DAS组合密封圈密封特性
夏毅敏1, 2,张欢1, 2,罗春雷1, 2,金耀3,曾雷1, 2,禹宏云1, 2
(1. 中南大学机电工程学院,湖南长沙,410083;2. 中南大学高性能复杂制造国家重点实验室,湖南长沙,410083;3. 湖南师范大学工程与设计学院,湖南长沙,410081)
为了研究工程机械用DAS组合密封圈密封特性及其变化规律,建立密封特性计算模型,使用三次多项式修正密封圈压力油侧接触应力,得到近似油膜压力分布;结合逆解法求解油膜厚度,研究DAS组合密封圈预压缩量、油液压力及活塞杆伸出速度对平均油膜厚度、内泄漏量及动摩擦力的影响。研究结果表明:随着预压缩量增大,平均油膜厚度及内泄漏量逐渐减小,动摩擦力逐渐增大;随着油液压力的增大,平均油膜厚度及内泄漏量逐渐减小,动摩擦力逐渐增大;随着活塞杆伸出速度增大,平均油膜厚度、内泄漏量及动摩擦力随之增大。综合考虑各因素对密封件磨损、内泄漏的影响,建议DAS组合密封圈应用于活塞密封时最小压缩量=1 mm,最大活塞杆伸出速度=0.1 m/s。
DAS组合密封圈;逆解法;油膜厚度;内泄漏量;动摩擦力
密封件失效是导致液压缸内泄漏故障的关键原因之一,国内外学者针对O形[1−2]、Y形[3−4]、滑环组合密封圈[5]等常见活塞密封圈进行了大量研究。对密封特性的研究大多采用逆解法求解雷诺方程获得润滑油膜厚度,计算内泄漏量与动摩擦力。但逆解法的一大难点是如何确定润滑状态下油膜压力分布。目前,常假设密封件在流体动力润滑状态下油膜的压力分布与干摩擦状态下的接触应力分布一致[6]。NIKAS等[7]将密封件材料简化为线弹性材料,采用广义胡克定理求解油膜压力分布;崔晓等[8]采用有限元软件ADINA计算油膜压力分布。考虑到大多数密封材料是超弹性体,在较大变形时简化为线弹性体进行分析不准确,而采用有限元分析能够方便、准确地计算密封件的接触应力。然而,根据油液压力大于接触应力密封失效的原理[9],通过有限元计算所得结果不能直接用于油膜厚度求解。这是由于不考虑介质存在时,通过有限元计算的密封圈压力油侧的接触应力存在小于油液压力的区域,而真实情况下该区域压力近似与油液压力相等。DAS(double acting seal)组合密封圈具有结构紧凑、双向密封性能良好及安装方便等优点,常用于起重机、盾构机等工程机械的活塞动密封[10],但人们对DAS组合密封圈的研究较少。为了准确地分析DAS组合密封圈的密封特性,本文作者采用有限单元法计算密封圈的初始接触应力,然后对接触应力进行三次多项式修正得到近似的油膜压力分布,最后采用逆解法计算油膜厚度、内泄漏量与动摩擦力。
1 密封特性数值计算模型
1.1 DAS组合密封圈简介
DAS组合密封圈由1个弹性齿状密封圈、2个附加挡圈和2个耐磨环组成,其结构示意图如图1所示。弹性齿状密封圈外侧面有3个密封唇:中间密封唇较宽作为主密封,2个外端密封唇作为附加性密封。内侧面呈弧形,沟槽的接触面较宽,作为静密封。将弹性齿状密封圈的上副密封唇、主密封唇、下副密封唇分别简称为上副唇、主唇、下副唇。
弹性齿状密封圈的材料常采用丁腈橡胶(NBR),挡圈的材料常采用聚氨酯弹性体(TPU),耐磨环的材料常采用填充聚甲醛(POM)。
1.2 油膜厚度计算模型
采用一维稳态等温雷诺方程描述DAS组合密封圈的润滑状态:

图1 DAS组合密封圈示意图

(2)

(4)

对式(1)进行移项变换得
(6)
则式(6)中括号内函数为常数,即

(8)
对式(8)进行微分整理得

(10)
将式(10)代入式(8)并整理得
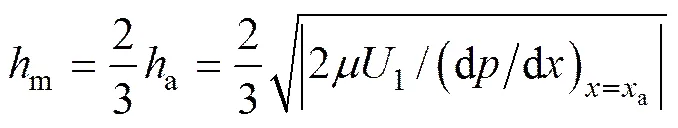
将式(11)代入式(8)即可求解关于油膜厚度的一元三次方程。由于通过有限单元法计算的干摩擦状态下的接触应力属于离散应力,可将式(8)在接触节点离散,将微分形式差分化,整理后的形式如下:
(12)
式中:p,x,h和分别为沿轴向第个接触节点的润滑油压力、轴向坐标、油膜厚度、动力黏度;为轴向接触节点的总数。通过有限单元法计算的接触应力是在不考虑油液存在的情况下,仅将油液压力施加在弹性齿状密封圈表面,分析过程仅考虑弹性齿状密封圈与缸筒的接触,而没有考虑弹性齿状密封圈与油液的接触,导致弹性齿状密封圈的接触应力在与缸筒接触的边缘为0[11]。假设流体动力润滑状态的油膜压力分布与干摩擦状态的接触应力分布相同,在实际情况下,当有油液作用在弹性齿状密封圈表面上时,油液压力大于接触应力的位置将发生密封失效,在该位置弹性齿状密封件与缸筒的接触将分离,油液将充满接触分离位置。从以上分析可知:通过有限单元法计算的干摩擦状态下密封圈压力油侧的接触应力与实际情况不相符。依据实际边界条件的特征,假设在干摩擦状态下接触起始点至接触应力大于油液压力接触点之间的油膜压力符合三次多项式分布[8]:

密封圈压力油侧满足如下边界条件:
(14)

(16)
将式(16)计算的系数代入式(13)即得干摩擦状态下压力油侧接触起始点至接触应力大于油液压力接触点之间的油膜压力分布。由于压力呈三次多项式分布,故还可以通过计算压力分布的拐点位置以计算式(11),至此所有未知参数都能通过假设和计算确定,油膜厚度也就可以求解。为了方便分析不同因素对油膜厚度的影响,取平均油膜厚度进行分析。油膜厚度计算流程如图2所示。
1.3 内泄漏量计算模型
通过数值计算得到的油膜厚度是各个接触节点的油膜厚度,属于离散值,故内泄漏流量的计算也可以通过计算各个接触节点处的内泄漏流量再取平均值,具体计算公式为

1.4 动摩擦力计算模型
当DAS组合密封圈处于流体动压润滑状态时,各个接触节点区域的黏性剪切应力计算式为

图2 油膜厚度计算流程

影响液压缸动摩擦力的剪切黏性力位于活塞外表面与油液接触位置,黏性剪切应力为
(19)
则总的内摩擦力计算式为

当油液压力作用在DAS组合密封圈时,不仅主唇与缸筒内壁发生接触,而且副唇与缸筒内壁发生接触,分别计算主唇动摩擦力fmain与副唇动摩擦力fvice,经求和可得DAS组合密封圈动摩擦力fDAS:
(21)
2 DAS组合密封圈接触应力分布规律
2.1 有限元模型的建立
Mooney−Rivlin 模型能够很好地描述橡胶材料在150% 以内的变形。该模型在小应变范围内具有较强的稳定性,工程上常作为有限元分析的首选模型[12]。模型的材料参数据文献[13−15]取值。弹性齿状密封圈的邵氏硬度为80,经计算得橡胶特性参数10=1.56 MPa,01=0.39 MPa。DAS组合密封圈各零部件材料属性如表1所示。

表1 DAS组合密封件各零部件材料属性
采用ABAQUS建立有限元模型时进行以下假设:1) 缸筒与活塞视为刚体;2) 橡胶材料是完全弹性且各向同性;3) 完全轴对称模型。缸筒与活塞采用轴对称解析刚体建模,简化为线。耐磨环、挡圈网格类型为CAX4,齿状密封圈网格类型为CAX4H。对缸筒施加径向负位移载荷,使齿状密封圈产生压缩,模拟DAS组合密封圈装配过程;对DAS组合密封圈与油液接触的部位施加压力载荷,模拟DAS组合密封圈静密封过程。DAS组合密封圈二维轴对称模型如图3所示,图中箭头作用表面表示加载区域。当副唇未与缸筒接触时,加载区域包含图3中黑色方框区域;当副唇与缸筒接触时,加载区域不包括图3中黑色方框区域。在整个分析过程中,活塞保持固定。

图3 DAS组合密封圈有限元模型
2.2 有限元结果分析
在油液压力作用下,弹性齿状密封圈主唇及下副唇与缸筒发生接触。在初始压缩量=1.5 mm时,不同压力对弹性齿状密封圈主唇接触应力分布的影响如图4所示。

油液压力p/MPa:1—5;2—10;3—15;4—20;5—25。
从图4可以看出:随着油液压力的增大,主唇密封处的接触应力和接触宽度随之增大;最大接触应力位置偏向下副唇,沿两侧逐渐减少;最大接触应力随压力增大而增大,接触宽度随压力增大趋势变缓。
在初始压缩量=1.5 mm时,不同油液压力对弹性齿状密封圈下副唇接触应力分布的影响如图5所示。

油液压力p/MPa:1—5;2—10;3—15;4—20;5—25。
从图5可以看出:随着油液压力的增大,下副唇密封处的接触应力和接触宽度随之增大;在下副唇与缸筒最初接触节点的接触应力最大,沿两侧逐渐减少,最大接触应力随压力增大而增大,接触宽度随压力增大趋势变缓。
3 密封特性数值计算结果分析
当预压缩量=1.5 mm时,不同油液压力和活塞杆伸出速度对平均油膜厚度、内泄漏量及动摩擦力的影响见图6。

(a) 平均油膜厚度;(b) 内泄漏量;(c) 动摩擦力
从图6(a)可以看出:随着油液压力增大,平均油膜厚度逐渐减小;当油液压力≥10 MPa时,平均油膜厚度减小趋势变缓;随着活塞杆速度增大,平均油膜厚度逐渐增大。从图6(b)可以看出:随着油液压力增大,内泄漏量逐渐减小;随着速度增大,内泄漏量逐渐增大。从式(17)可知:内泄漏由压差流与剪切流2部分组成,当压力增大时,油膜厚度减小,且油膜厚度处于微米级与亚微米级,内泄漏主要由剪切流引起,而剪切流与油膜厚度、速度成正比;在相同速度下,压力增大,油膜厚度减小,剪切流引起的内泄漏量减小;在相同压力下,速度增大,油膜厚度增大,内泄漏量增大;当≥0.1 m/s时,油膜厚度增大速度变快,内泄漏量的增大也随之变快;当≥10 MPa时,内泄漏量随压力变化的趋势变缓,这与平均油膜随压力的变化趋势一致。当活塞杆伸出速度≤0.1 m/s时,内泄漏量随油液压力的增大几乎不发生改变。从图6(c)可以看出:随着油液压力及速度增大,动摩擦力逐渐增大。从式(20)可知:动摩擦力由压差流动及剪切流动综合所致,在相同速度下,压力增大,油膜厚度减小,油液密度与黏度增加;当压力较小时,由剪切流引起的动摩擦力占主导并随之增大;当压力较大时,油膜厚度减小的趋势变缓,动摩擦力的增大趋势也趋于平缓;在相同压力下,速度增大,油膜厚度增大,动摩擦力增大;当≥0.1 m/s时,油膜厚度增大速度变快,动摩擦力的增大趋势也随之变快。
当速度过大时,动摩擦力的增大会造成密封处油温升高,引起油液黏度下降,油膜厚度变薄,加剧密封件的磨损,并且速度增大会加剧内泄漏,这样,在使用时就存在1个合适的使用速度。经综合考虑,取=0.1 m/s作为最大运行速度。
当活塞杆伸出速度=0.1 m/s时,不同油液压力和预压缩量对平均油膜厚度、内泄漏量及动摩擦力的影响如图7所示。
从图7可以看出油液压力对密封特性的影响与图6所示的影响一致,这里只分析预压缩量对密封特性的影响。从图6(a)可见:随着预压缩量增大,平均油膜厚度逐渐减小。这是因为在相同油液压力作用下,随着预压缩量增大,接触应力会增大,造成油膜厚度减小。从图6(b)可以看出:随着预压缩量增大,内泄漏量逐渐减小。这是因为预压缩量的增大会使油膜变薄,油膜变薄造成内泄漏量减小。从图6(c)可以看出:随着预压缩量增大,动摩擦力逐渐增大。这是因为本文假设密封件处于完全动力润滑状态,在相同压力下,当预压缩量增大时,接触应力增大,油膜变薄,油液密度、黏度增大,油膜内摩擦引起的动摩擦力增大。

(a) 平均油膜厚度;(b) 内泄漏量;(c) 动摩擦力
当预压缩量过大时,动摩擦力增大会造成密封处油温升高,引起油液黏度下降,使油膜厚度减少,加剧密封件的磨损,同时考虑到压缩量减少会增大内泄漏量,故设计时存在1个合适的压缩量。经综合考虑,可取=1 mm作为最小压缩量。
4 试验研究
为了验证油液压力、活塞杆伸出速度对内泄漏量及动摩擦力的影响,进行相关型式试验。图8所示为试验台结构原理图,图9所示为试验台传感器安装示意图。

1—基座;2—支腿油缸;3—连杆;4—铰接;5—动力油缸。

图9 试验台传感器安装示意图
4.1 测试原理
活塞杆伸出时无杆腔连续性方程如下:

式中:为内泄漏量;1为无杆腔流量;1为无杆腔面积,1=9.5×10−3m2;为活塞杆伸出位移;1为等效容腔体积,1=2.65×10−3m3;为体积弹性模量,=2×10−9Pa;1为无杆腔压力。通过连续采集无杆腔流量、无杆腔压力、活塞杆伸出位移信号就可以求解实时的内泄漏量。
液压缸动力平衡方程如下:
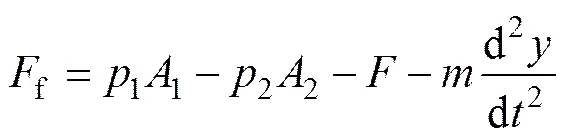
(24)
式中:2为有杆腔压力;为负载;为连杆弹性模量,=2.1×1011Pa;为连杆轴向应变;为连杆截面积,=7.24×10−3m2;为活塞与活塞杆装配件质量,=50 kg。通过连续采集无杆腔压力、有杆腔压力、连杆轴向应变、活塞杆伸出位移信号就可以求解实时的动摩擦力。
4.2 试验结果分析
图10所示为压缩量=1.5,=10 MPa时不同活塞杆伸出速度对DAS组合密封圈内泄漏量及动摩擦力的影响。

1—动摩擦力;2—内泄漏量。
从图10可以看出动摩擦力及内泄漏量随速度的增大而增大。当=1.5,=0.015 m/s时,不同油液压力对DAS组合密封圈内泄漏量及动摩擦力的影响见图11。

1—动摩擦力;2—内泄漏量。
从图11可以看出:动摩擦力随油液压力的增大而增大,内泄漏量随油液压力增大而减小。动摩擦力与内泄漏试验结果比数值计算结果偏大,其原因是:一方面,建模时未考虑活塞杆的密封,导致动摩擦力偏大;另一方面,传感器的精度偏低,误差较大。
5 结论
1) 提出了一种新颖的计算液压缸密封件动力润滑油膜厚度的计算方法。针对工程机械用DAS组合密封圈,采用有限单元法计算接触应力,并采用三次多项式对密封圈压力油侧接触应力进行修正,结合逆解法求解一维常温稳态雷诺方程,数值计算结果证明该计算方法可行。
2) 随着油液压力增大,平均油膜厚度及内泄漏量逐渐减小,动摩擦力逐渐增大;随着预压缩量增大,平均油膜厚度及内泄漏量随之减少,动摩擦力随之增大;随着活塞杆伸出速度增大,平均油膜厚度、内泄漏量及动摩擦力随之增大。
3) 综合考虑各因素对密封件磨损、内泄漏的影响,建议DAS组合密封圈应用于活塞密封的最小压缩量为=1 mm,最大活塞杆伸出速度=0.1 m/s。
[1] 关文锦, 杜群贵, 刘丕群. 橡胶O形圈密封性能的有限元分析[J]. 润滑与密封, 2012, 37(6): 60−64.GUAN Wenjin, DU Qungui, LIU Piqun. Finite element analysis of the sealing performance of rubber O-ring[J]. Lubrication Engineering, 2012, 37(6): 60−64.
[2] STUPKIEWICZ S, MARCINISZYN A. Elastohydrodynamic lubrication and finite configuration changes in reciprocating elastomeric seals[J]. Tribology International, 2009, 42(5): 615−627.
[3] 王世强, 张付英, 张东葛. 基于ANSYS的Y形密封圈密封性能研究[J].润滑与密封, 2012, 37(12): 61−64.WANG Shiqiang, ZHANG Fuying, ZHANG Dongge. Study on sealing performance of Y-ring based on ANSYS[J]. Lubrication Engineering, 2012, 37(12): 61−64.
[4] THATTE A, SALANT R F. Transient EHL analysis of an elastomeric hydraulic seal[J]. Tribology International, 2009, 42(10): 1424−1432.
[5] 陈国定, HAISER H, HASS H, 等. 阶梯组合密封件的力学性能研究[J]. 机械科学与技术, 2000, 19(6): 920−922.CHEN Guoding, HAISER H, HASS H, et al. Study of mechanical performances of step seals[J]. Mechanical Science and Technology, 2000, 19(6): 920−922.
[6] 海因茨K. 米勒, 伯纳德S. 纳乌. 流体密封技术—原理与应用[M]. 北京: 机械工业出版社, 2002.MULLER H K, NAU B S. Fluid sealing technology principles and applications[M]. Beijing: China Machine Press, 2002.
[7] NIKAS G K, SAYLES R S. Study of leakage and friction of flexible seals for steady motion via a numerical approximation method[J]. Tribology International, 2006, 39(9): 921−936.
[8] 崔晓, 董彦良, 赵克定. 基于ADINA的组合式动密封泄漏量与摩擦力计算术[J]. 华南理工大学学报(自然科学版), 2010, 38(2): 95−100. CUI Xiao, DONG Yanliang, ZHAO Keding. Calculation of leakage and friction of combined dynamic seals based on ADINA[J]. Journal of South China University (Science and Technology), 2010, 38(2): 95−100.
[9] 刘明, 陆军, 段栋. Y 型密封圈密封原理探讨与结构优化设计[J]. 特种橡胶制品, 2012, 33(3): 57−59. LIU Ming, LU Jun, DUAN Dong. Research about sealing principle and structure optimization of Y-ring[J]. Special Purpose Rubber Products, 2012, 33(3): 57−59.
[10] 徐林平. 山形组合密封圈的特点及其应用[J]. 液压与气动, 2002(1): 42−43.XU Linping. The characteristic of mountain shaped compact seal and its application[J]. Hydraulic and Pneumatic, 2002(1): 42−43.
[11] KIM H K, NAMB J H, HAWONG J S, et al. Evaluation of O-ring stresses subjected to vertical and one side lateral pressure by theoretical approximation comparing with photoelastic experimental results[J]. Engineering Failure Analysis, 2009, 16(6): 1876−1882.
[12] 王国权, 刘萌, 姚艳春, 等. 不同本构模型对橡胶制品有限元法适应性研究[J]. 力学与实践, 2013, 35(4): 40−47.WANG Guoquan, LIU Meng, YAO Yanchun, et al. Application of different constitutive models in the nonlinear finite element method for rubber parts[J]. Mechanics in Engineering, 2013, 35(4): 40−47.
[13] 陈国强, 谭建平, 陈晖. 高压大流量水阀U形密封圈失效机理[J]. 中南大学学报(自然科学版), 2013, 44(3): 942−948.CHEN Guoqiang, TAN Jianping, CHEN Hui. Failure mechanism of U-ring seal in water valve with high pressure and large flow capacity[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 942−948.
[14] 郑明军, 王文静, 陈政南, 等. 橡胶Mooney-Rivlin模型力学性能常数的确定[J]. 橡胶工业, 2003, 50(8): 462−465. ZHENG Mingjun, WANG Wenjing, CHEN Zhengnan, et al. Determination for mechanical constants of rubber Mooney-Rivlin model[J]. China Rubber Industry, 2003, 50(8): 462−465.
[15] LEE B S, RIVIN E I. Finite element analysis of load-deflection and creep characteristics of compressed rubber components for vibration control devices[J]. Journal of Mechanical Design, 1996, 118(3): 328−335.
(编辑 陈灿华)
Sealing performance research of DAS composition seal ring
XIA Yimin1, 2, ZHANG Huan1, 2, LUO Chunlei1, 2, JIN Yao3, ZENG Lei1, 2, YU Hongyun1, 2
(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China;3. College of Engineering and Design, Hunan Normal University, Changsha 410081, China)
In order to study sealing performance and variation law of DAS composition ring used for engineering machinery, sealing performance calculation model was built. By applying cubic polynomial to correct contact stress, approximate pressure distribution was obtained. With the inverse method, film thickness was calculated. Finally, the influence of pre-compression, pressure and out velocity on average film thickness, internal leakage and dynamic friction were investigated. The results show that with the increase of the pre-compression, average film thickness and leakage rate decrease, while dynamic friction increases. When pressure increases, average film thickness and leakage rate decrease, but dynamic friction increases. With the increase of out speed, average film thickness, leakage flow rate and dynamic friction also increase. Taking the influence of various factors on wear and leakage into consideration, it is suggested that the lowest pre-compression is 1 mm and the largest velocity is 0.1 m/s when it is used for piston sealing.Key words: DAS composition seal ring; inverse method; film thickness; leakage flow rate; dynamic friction
10.11817/j.issn.1672-7207.2017.01.013
TH117.2
A
1672−7207(2017)01−0091−08
2016−03−10;
2016−05−12
湖南省科技专项计划项目(2014FJ1002);国家高技术研究发展计划(863计划)项目;湖南省战略性新兴产业科技攻关类项目(2016GK4009) (Project(2014FJ1002) supported by Science and Technology Plan of Hunan Province; Project(2013AA040203) supported by the National High-tech R&D Program (863 Program); Project(2016GK4009) supported by the Strategic Emerging Industries Science and Technology Research of Hunan Province)
夏毅敏,博士,教授,从事流体传动与控制、掘进设备设计研究;E-mail: xiaymj@csu.edu.cn

