TBM盘形滚刀磨损预测模型

谭青，孙鑫健，夏毅敏，蔡小华，朱震寰，张晋浩



TBM盘形滚刀磨损预测模型

谭青1, 2，孙鑫健1, 2，夏毅敏1, 2，蔡小华1, 2，朱震寰1，张晋浩1

(1. 中南大学高性能复杂制造国家重点实验室，湖南长沙，410083；2. 中南大学机电工程学院，湖南长沙，410083)

为了研究TBM盘形滚刀破岩过程中的磨损行为，首先通过分析刀具与刀盘的运动规律推导等截面盘形滚刀运动学公式，结合磨粒磨损理论及刀岩接触力学模型建立盘形滚刀磨损预测模型，并利用MATLAB软件开发滚刀磨损量的预测模拟程序。将该模型应用到某引水工程中对滚刀磨损过程进行仿真，得到盘形滚刀的磨损形貌演变规律。研究结果表明：仿真磨损量与实测磨损量随刀位号变化趋势基本一致，刀盘上各个安装位置处仿真预测的滚刀刀圈正面及侧面磨损值与实测值的平均相对误差分别为18%和30%。刀刃逐渐磨损成尖形，所得磨损形态与工程实际观测相吻合。

TBM；盘形滚刀；磨损预测；数值仿真

全断面岩石隧道掘进机(TBM)目前广泛应用于岩石地层的隧道开挖，盘形滚刀作为TBM破岩的核心部件，在开挖过程中需要承受极大的推进力以及与岩石之间的摩擦力，极易产生严重磨损[1]。大量的工程数据表明：掘进机刀具检查、更换等作业时间占施工总时间的30%~40%[2]，因此，提高其磨损寿命是TBM设计、制造及施工中的关键技术问题。国内外学者对盘形滚刀磨损行为的研究方法主要是实验研究，即对标准试样进行试验机模拟从而获得材料的耐磨性，并提出了大量的磨耗性实验方法[3−5]，其中Cerchar磨蚀指数常用于表征岩石的磨耗性[6]，但是由于摩擦学系统的复杂性和工况的不同，试验研究的周期长成本高，特别是在磨损寿命预测这种随时间不断演化的过程。磨损仿真提供了一种新的研究手段[7]，其核心思想是将动态的磨损过程离散化，每一离散的磨损状态就能被认为是稳态阶段，然后利用磨损的基本理论解决磨损预测问题。磨损仿真目前正逐渐应用于各个领域，并取得大量研究成果，如CHANG等[8]对轮轨磨耗进行数值仿真分析，获得了轮轨磨损形态的变化过程；罗仁等[9]在FASTSM软件中嵌入磨损模型对高速列车车轮磨耗问题也进行了研究；江亲瑜等[10−11]建立了铰链机构、凸轮机构摩擦副的全寿命磨损过程仿真软件；HEGADEKATTE等[12−14]将Archard磨损模型嵌入到Abaqus软件中对微型齿轮的磨损过程进行仿真，采用微观磨损模型对齿轮副全寿命磨损过程进行了仿真，并取得了较好的效果。本文作者采用了磨损仿真的方法，在滚刀接触面运动学、破岩机理分析的基础上，通过设定磨损步长实现磨损过程的离散化，运用MATLAB数值仿真技术建立盘形滚刀磨损数值模拟模型，对刀刃的正面及侧面磨损过程、刀刃磨损形态演变过程进行研究，并进行工程验证。

1 盘形滚刀磨损预测模型

磨损是一个连续的过程，摩擦学元素的性质是时间依赖的，对于盘形滚刀与岩石摩擦副来说，其各个元素特性比如接触应力、接触区温度、接触区相对滑动速度都是随时间变化的[15]。在这种条件下实现磨损仿真的先决条件是把连续的磨损过程离散化，研究摩擦副在运动过程中的一系列离散状态。本文将滚刀滚压岩石一圈过程中刀圈的微元磨损量视为一个磨损步长，并考虑2个步长之间的变化过程，将摩擦副上某点的矢径加上磨损矢量得到新点的矢径，通过欧拉方法把磨损步长对滑动微元位移进行积分得到总的磨损量。磨损方向为表面内法线方向，如图1所示。

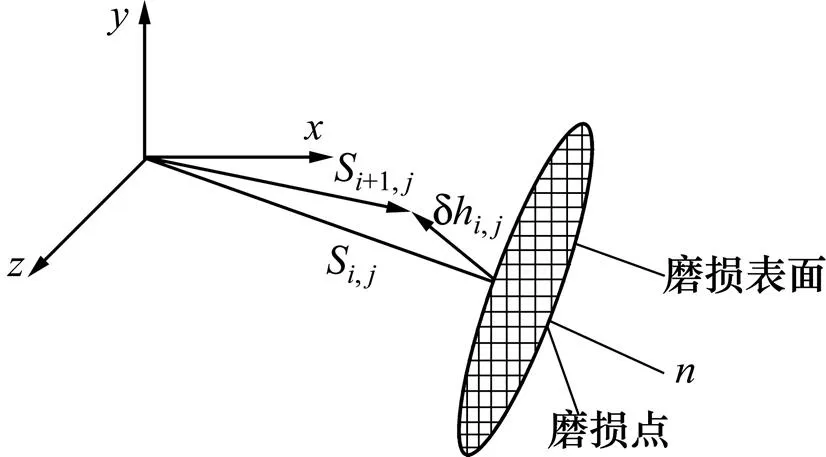
图1 局部磨损模型

零件从一个状态逐步向另一种状态的动态变化过程采用文献[16]的方法，表示为

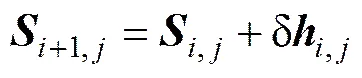
磨损步长通过磨料磨损公式[17]变形得到

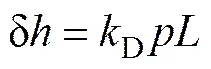
1.1 运动学模型

KOLYMBAS[18]指出尽管盘形滚刀破岩过程中处于滚动状态，盘形滚刀上各点的速度却与岩石切面之间存在夹角，产生相对滑动，这是导致盘形滚刀磨损的主要原因，如图2所示。图2中：为滚刀实际速度；slip为相对滑动速度。因此，将滚刀与岩石接触区域分为刀圈正面与刀圈侧面2部分，计算刀圈与岩石接触区任一点相对于岩石切面的相对滑动速度，通过积分来计算一个步长时间内滚刀与岩石的相对滑动长度。

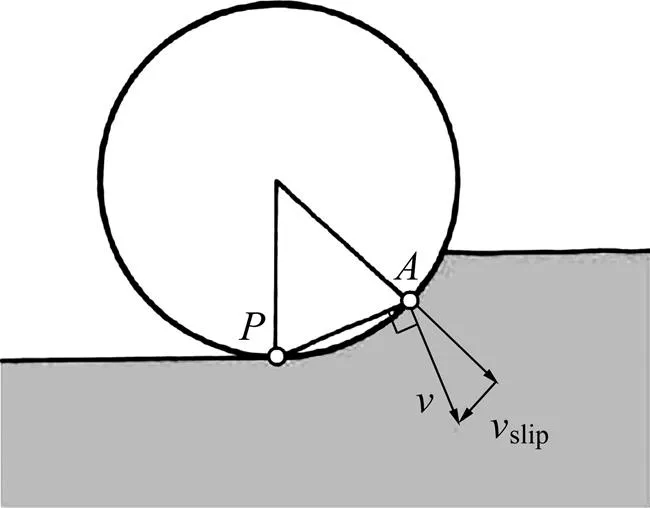
图2 盘形滚刀磨损原因图

盘形滚刀的运动主要可以分为刀盘运动与盘形滚刀相对于刀盘旋转2部分，现假设刀盘进给速度为v，旋转角速度为ω1，盘形滚刀自转角速度为ω。为了简化分析，将盘形滚刀的空间运动转化为平面运动，滚刀以一定的速度沿直线滚压岩石，滚刀破岩最深点为其速度瞬心，盘形滚刀绕该点做纯滚动运动,从而滚刀上任一点实际运动速度可以分解为3个运动。分运动1：绕盘形滚刀表面处于破岩最深处的点构成的线的转动，转动角速度为ω；分运动2：平行于刀盘轴线方向的转动，转轴为平行于刀盘轴线且过盘形滚刀中心的轴线，转动速度为ω1；分运动3：指向刀盘推进方向的平动，速度为v。滚刀刀圈上任一点的速度均可以由3个方向上的分运动速度求矢量和得到，盘形滚刀的运动分解示意图如图3所示。

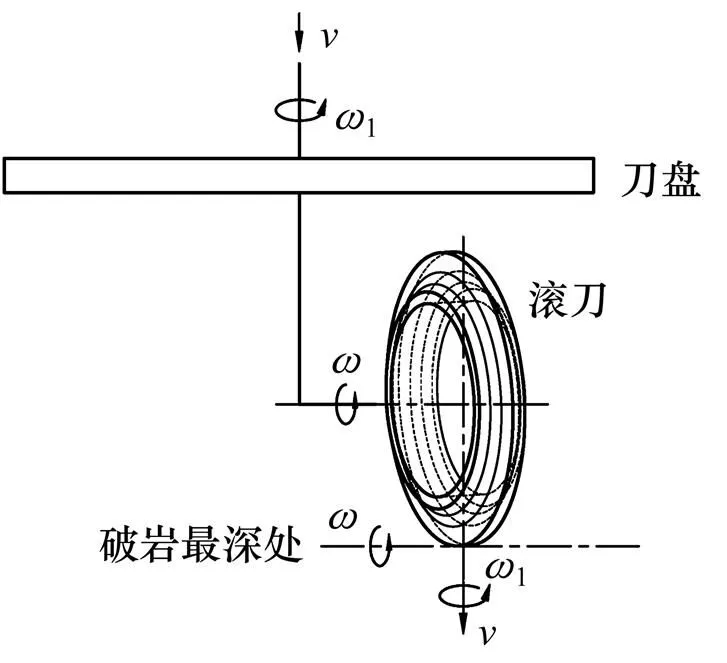
图3 盘形滚刀运动分解

1.1.1 盘形滚刀刀圈正面与岩石接触过程分析

图4所示为刀圈正面与岩石接触情况示意图，其中点为刀圈正面与岩石接触线上一点，为刀圈半径，弧线表示刀圈正面与岩石接触面的投影曲线v1，v2和v3分别为点分运动1、分运动2和分运动3导致的分速度，从而点的绝对速度为

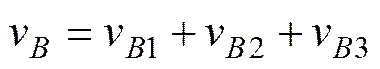
式中：v1为垂直于图4中线指向岩石的速度；v2为垂直于图4中−平面的速度；v3为指向轴正向的速度。

考虑分运动1，由于v1与破岩切面之间存在夹角，点与岩石表面会产生相对滑动，相对滑动速度为

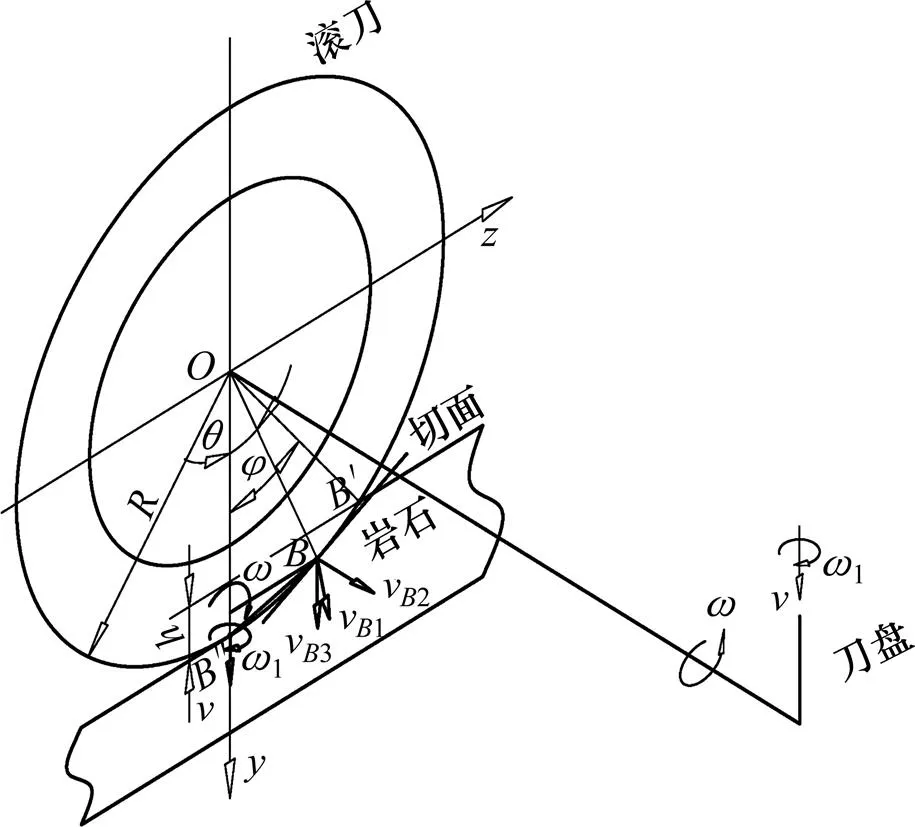
图4 盘形滚刀正面与岩石接触分析图

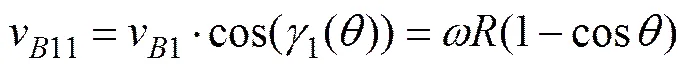
考虑分运动2，点分速度为

(5)

考虑分运动3，B3与破岩切面存在夹角，点与岩石表面会产生相对滑动，相对滑动速度为

滚刀每转1圈，刀圈正面点沿着滚刀圆周方向从点滑到点，之后便脱离接触区，不再产生磨损。该接触过程中由于具有相对滑动，该相对滑动量导致其磨损。因此，滚刀转1圈点与岩石接触时间可以定为接触角与滚刀自转角速度的比值。

刀圈正面相对滑动量可以表示为

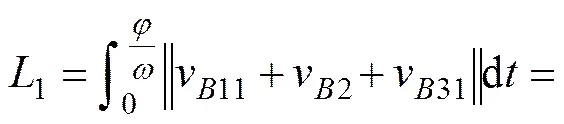
(7)

1.1.2 盘形滚刀刀圈侧面与岩石接触过程分析

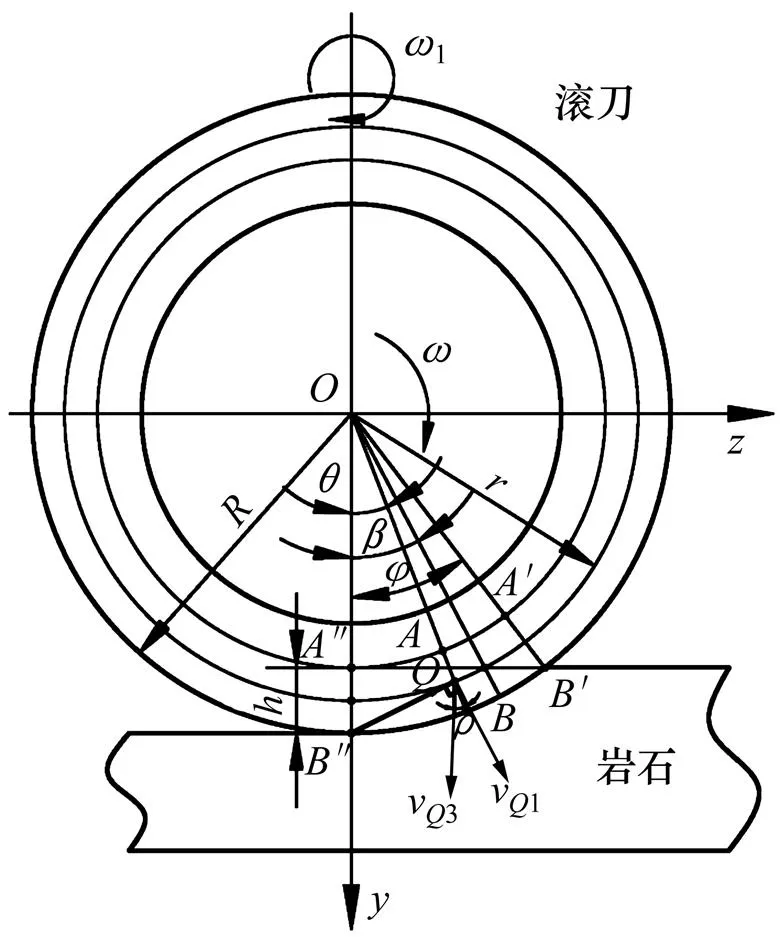
图5 盘形滚刀侧面与岩石接触分析图

取侧面线上点(,)，＜＜，。

点的速度为分运动1导致的分速度Q1、分运动2导致的分速度Q2、分运动3导致的分速度Q3的矢量和：

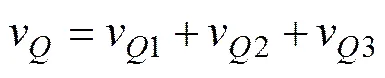
侧面点运动分析方法与正面相似，所不同的是分运动2当中点会挤压岩石但是不会发生相对滑动运动，故分运动2导致的滑动速度为0 m/s。盘形滚刀侧面上点与岩石相对滑动量为

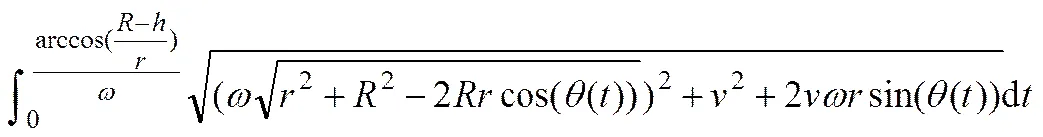
1.2 接触力学模型

盘形滚刀刀圈表面与岩石的接触力模型是滚刀磨损预测及受力预测理论的核心问题，故本文选择了CSM载荷预测模型进行计算[19−20]，模型公式如下：

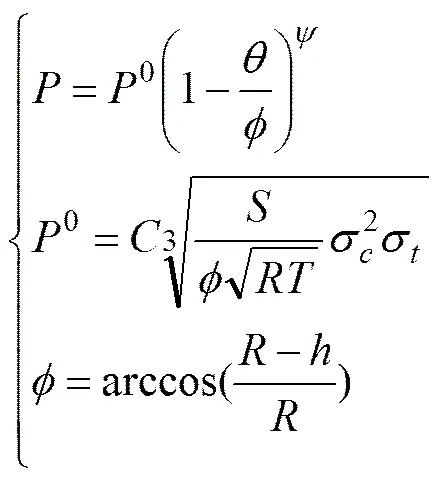
式中：为试验滚刀半径；为刀圈顶刃宽度；为刀圈顶刃压力分布系数(对于等截面盘形滚刀及磨钝后的盘形滚刀，接近0，对于尖刃盘形滚刀，=0.2)；为刀圈讨论破碎区压应力；为岩石抗拉强度；为滚刀刀间距；为系数；为岩石单轴抗压强度。

选择屠昌峰[21]刀圈侧面与岩石的接触应力的模 型，表达式如下：

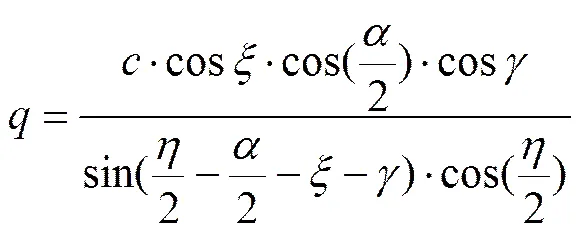
式中：q为刀圈侧面上某点与岩石接触应力；c为岩石内聚力；ζ为岩石内摩擦角；为盘形滚刀刀刃角；γ为岩石与盘形滚刀表面的摩擦角；η为岩石破碎角。

1.3 磨损步长计算

基于式(2)以及运动学模型、接触力学模型，可得刀圈正面磨损步长为

(12)

滚刀侧面磨损步长为

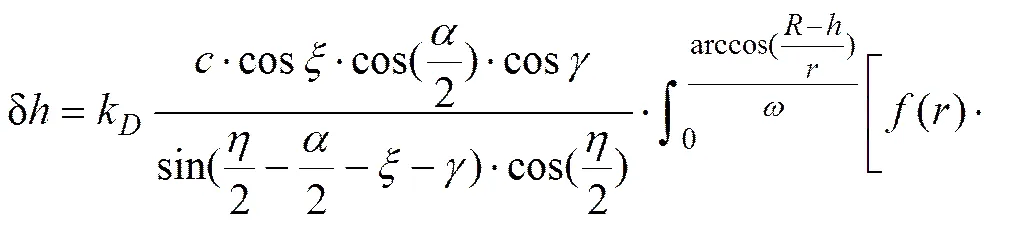
(13)

1.4 磨损仿真流程

利用Matlab软件编写了相应的计算程序，对盘形滚刀刀圈的正面及侧面进行磨损量计算，首先将盘形滚刀刀圈投影其中面上得到一个二维轮廓，磨损发生在刀圈与岩石接触区。仿真时，先将正面线及侧面线划分成许多网格点，计算每个点的相对滑动长度以及接触压力，根据磨损公式计算该点的磨损步长，然后对刀圈正面及侧面各网格节点进行位置更新，基于新的位置再次进行计算，不断进行迭代，最终得到一定掘进长度内滚刀刀圈最终磨损形态，具体仿真流程如图6所示。

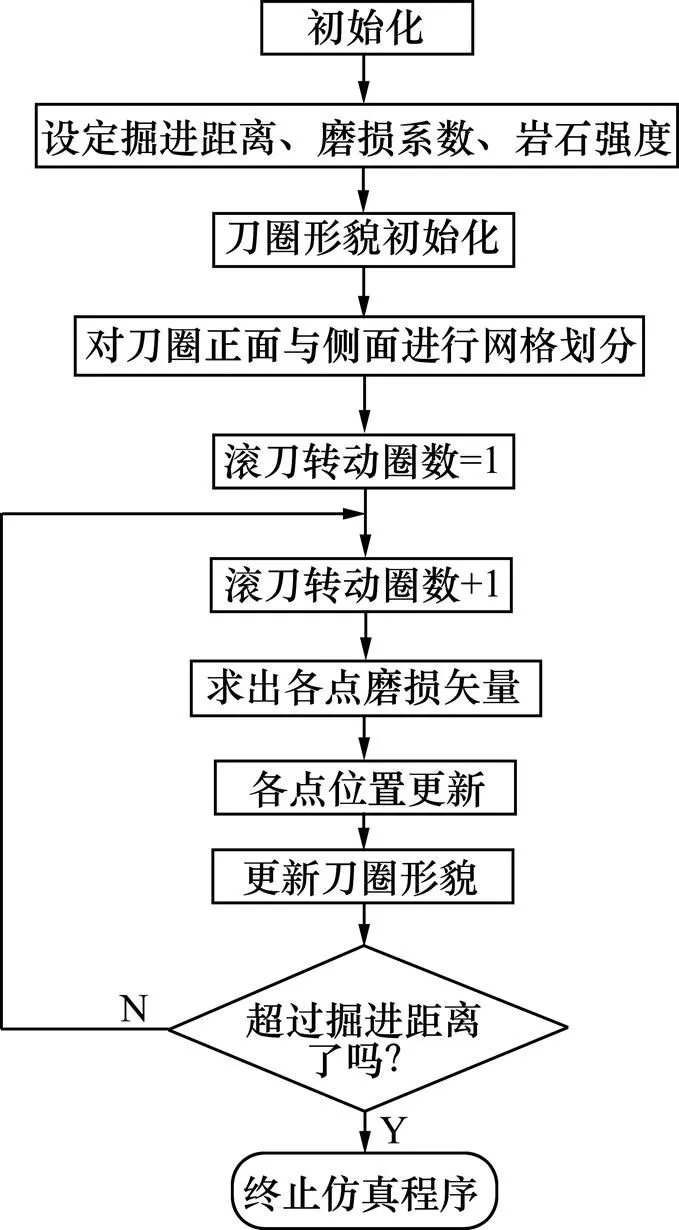
图6 磨损仿真流程图

2 仿真实例及结果

2.1 仿真条件

盘形滚刀的磨损受到盘形滚刀安装位置、刀盘掘进参数以及围岩地质条件的影响。某隧道工程采用TBM进行施工，其沿线地层主要由砂岩、含砾砂岩、砂砾岩、大理岩、云母石英片岩等组成，隧洞内所用管片为1.6 m型号，即掘进1环相当于掘进1.6 m。仿真主要针对工程第7 681~7 696环的磨损行为，该16环区段内岩石类型为前震旦系大理岩，其岩石力学性质如下：单轴抗压强度为58~64 MPa, 抗拉强度为4~6 MPa，内聚力为1.15 MPa，内摩擦角为43.5°，与钢的摩擦角为18°，破碎角为154°，Cerchar磨蚀指数为(CA)1.26。

目前，Cerchar磨蚀指数在工程界，特别是TBM盘形滚刀磨损预测中应用较多，它能较好地代表岩石的磨耗性，因此，将Cerchar磨蚀指数转化为三维磨损系数，以此作为中磨损率的计算依据。本文基于磨料磨损理论将Cerchar磨蚀指数转化为与接触区压力无关的磨损系数，通过磨料磨损公式[17]可以得到

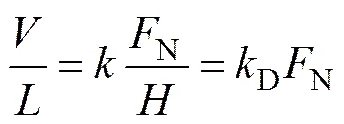
式中：为销的体积磨损量；为相对滑动长度；N为两者间正压力；为钢针硬度；为磨损系数，它包括微凸体几何形状及给定微凸体的剪切概率；D为三维磨损系数。

在CAI实验过程中，压力为70 N，相对滑动长度为0.01 m，可以得到

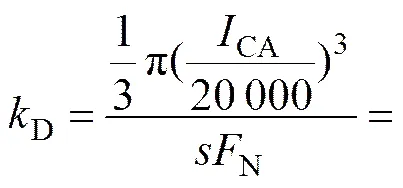
滚刀结构参数、刀盘配置参数、刀盘平均掘进参数如表1~3所示。

表1 盘形滚刀刀圈结构参数

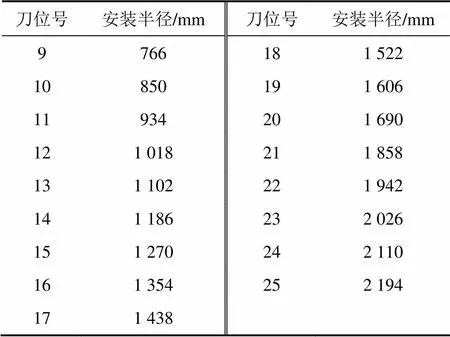
表2 刀盘配置参数

表3 平均掘进参数

2.2 磨损量仿真值与实测值

刀盘上正滚刀的磨损速度与其安装半径密切相关，同样掘进长度内，滚刀的转动速度及掘进路程随着安装半径的增大而增大，因此磨损量增大。图7所示为刀盘上9~25号正滚刀掘进16环后刀圈正面磨损仿真值及侧面磨损仿真值与实测值对照。

图7所示的正面磨损量仿真值与实测值随刀位号变化趋势相同，相对误差平均值为18%；侧面磨损量仿真值与实测值变化趋势亦相同，相对误差平均值达到30%，可见仿真模型对于盘形滚刀刀圈磨损预测值与实测值存在不小的误差。究其原因，主要是测量误差与模型误差两方面导致的。实际工况下由于现场测量工具有限，精度不高，测量环境恶劣，因此，会导致一定的测量误差。模型误差原因主要有3个：1) 磨损系数合理取值。本文所采用的磨损系数是通过采用平均的CA来计算的，而实际的磨损系数的取值与接触环境有着极大的关系，环境一旦发生变化，磨损系数会不断发生变化，且仿真模型中CA对于磨损系数的计算具有三次方放大效应，因此，磨损系数的不准确性会对磨损量的计算产生极大的影响。2) 本文所采用的接触力计算主要是CSM接触应力模型及屠昌 锋[21]模型，随着滚刀磨损形貌的不断变化，其基于的一些前提条件会逐步变得不适应，所得出的接触力与实际当中会发生较大差别，从而影响预测模型的准确性。3) TBM掘进过程中盘形滚刀与岩石接触过程的复杂性，表现为盘形滚刀并不确定是以刀尖贯入岩石最深处为速度零点，大量的工程实践表明盘形滚刀经常无法转动发生偏磨，因此，仿真中接触区各点的相对滑移量与实际值会有一定差别，但大致预测变化趋势合理。

(a) 正面磨损量；(b) 侧面磨损量

2.3 磨损演变图谱

对刀盘上18号盘形滚刀进行了仿真分析，图8所示为TBM掘进600 m过程中18号盘形滚刀刀刃轮廓外貌磨损变化的仿真结果。由图8可以看出：随着刀盘的不断掘进，滚刀一直处于动态磨损当中，刃型逐渐发生变化，刀尖宽度逐步减小直至最终滚刀变成尖刃。

1—起始边界；2—142 m；3—284 m；4—426 m；5—600 m。

对比仿真结果与工程实际结果可以发现：本文仿真所得出的滚刀磨损形貌演变符合实际情况，最终刃型也极其相似，因此，可以认为本文所建立的磨损预测模型反映了实际工况下盘形滚刀形貌演变规律。

3 结论

1) 运用了磨损仿真的方法，在磨粒磨损理论的基础上，结合盘形滚刀运动学模型和滚刀岩石接触力模型建立了盘形滚刀磨损预测模型，利用MATLAB 语言开发了相应的磨损预测程序，对盘形滚刀的磨损演变过程进行了模拟。

2) 对某隧道工程中大理石岩层的掘进工况进行了滚刀磨损仿真和实时测量，仿真预测值与实测值基本相符，且各刀位变化趋势基本一致。由于仿真条件与实际运行状态有差异，仿真结果与实测值有一定的误差，正面磨损量相对误差平均值达到18%，侧面磨损量相对误差平均值达到30%，但是变化趋势一致。研究发现在该种较软地层中盘形滚刀在正面磨损与侧面磨损同时作用下，刀刃逐渐磨损成尖形，与实际施工中滚刀磨损后的形貌一致。

[1] 张珂, 王贺, 吴玉厚, 等. 全断面硬岩TBM滚刀磨损关键技术分析[J]. 沈阳建筑大学学报(自然科学版), 2009, 25(2): 351−354. ZHANG Ke, WANG He, WU Yuhou, et al. Analysis on key wear technology of the TBM disc cutter[J]. Journal of Shenyang Jiangzhu University (Natural Science), 2009, 25(2): 351−354.

[2] 张厚美. 盾构盘形滚刀损坏机理的力学分析与应用[J]. 现代隧道技术, 2011, 48(1): 61−65. ZHANG Houmei. Mechanical analysis of tbm disc cutter damage mechanism and its application[J]. Modern Tunnelling Technology, 2011, 48(1): 61−65.

[3] DAHL F, BRULAND A, JAKOBSEN P D, et al. Classifications of properties influencing the drillability of rocks, based on the NTNU/SINTEF test method[J]. Tunnelling and Underground Space Technology, 2012, 28: 150−158.

[4] KÖHLER M, MAIDL U, MARTAK L. Abrasiveness and tool wear in shield tunnelling in soil/Abrasivität und Werkzeugverschleiß beim Schildvortrieb im Lockergestein[J]. Geomechanics and Tunnelling, 2011, 4(1): 36−54.

[5] DAHL F, GRØV E, BREIVIK T. Development of a new direct test method for estimating cutter life, based on the Sievers’ J miniature drill test[J]. Tunnelling and Underground Space Technology, 2007, 22(1): 106−116.

[6] MICHAEL A. Stress dependency of the Cerchar abrasivity index (CAI) and its effects on wear of selected rock cutting tools[J]. Tunnelling and Underground Space Technology, 2008, 23(4): 351−359.

[7] 汪选国, 严新平, 李涛生, 等. 磨损数值仿真技术的研究进展[J]. 摩擦学学报, 2004, 24(1): 188−192. WANG Xuanguo, YAN Xinping, LI Taosheng, et al. Research status of wear numerical simulation technology[J]. Tribology, 2004, 24(1): 188−192.

[8] CHANG Chongyi, WANG Chengguo, JIN Ying. Study on numerical method to predict wheel/rail profile evolution due to wear[J]. Wear, 2010, 269(3/4): 167−173.

[9] 罗仁, 曾京, 戴焕云, 等. 高速列车车轮磨耗预测仿真[J]. 摩擦学学报, 2009, 29(6): 551−558. LUO Ren, ZENG Jing, DAI Huanyun, et al. Simulation on wheel wear prediction of high-speed train[J]. Tribology, 2009, 29(6): 551−558.

[10] 江亲瑜, 李宝良, 易风, 等. 基于数值仿真技术求解铰链机构磨损概率寿命[J]. 机械工程学报, 2007(1): 196−201. JIANG Qinyu, LI Baoliang, YI Feng, et al. Probabilistic wear lifetime of hinge configurations resolved on numerical simulation[J]. Chinese Journal of Mechanical Engineering, 2007(1): 196−201.

[11] 江亲瑜, 易风, 李玉光, 等. 铰链机构磨损的数值仿真[J]. 中国机械工程, 2005(2): 8−11. JIANG Qinyu, YI Feng, LI Yuguang, et al. Numerical simulation on mild wear of hinge configurations[J]. Chinese Journal of Mechanical Engineering, 2005(2): 8−11.

[12] HEGADEKATTE V, HUBER N, KRAFT O. Development of a simulation tool for wear in microsystems[J]. Microengineering of Metals and Ceramics, 2008: 605−623.

[13] HEGADEKATTE V, HUBER N, KRAFT O. Modeling and simulation of wear in a pin on disc tribometer[J]. Tribology Letters, 2006, 24(1): 51−60.

[14] HEGADEKATTE V, KURZENHAUSER S, HUBER N, et al. A predictive modeling scheme for wear in tribometers[J]. Tribology International, 2008, 41(11): 1020−1031.

[15] 谢友柏. 摩擦学系统的系统理论研究和建模[J]. 摩擦学学报, 2010, 30(1): 1−8. XIE Youbai. On the system theory and modeling of tribo-systems[J]. Tribology, 2010, 30(1): 1−8.

[16] 李宝良. 先接触磨损数值仿真及应用研究[D]. 大连: 大连交通大学机械工程学院, 2010: 74−84.LI Baoliang. Research of numerical simulation and application of line contact wear[D]. Dalian: Dalian Jiaotong University. School of Mechanical Engineering, 2010: 74−84.

[17] HEGADEKATTE V, HILGERT J, KRAFT O, et al. Multi time scale simulations for wear prediction in micro-gears[J]. Wear, 2010, 268(1/2): 316−324.

[18] KOLYMBAS D. Tunnelling and tunnel mechanics[M]. Berlin Heidelberg: Springer, 2005: 235−271.

[19] ROSTAMI J, OZDEMIR L, NILSON B. Comparison between CSM and NTH hard rock TBM performance prediction models[C]// Proceedings of Annual Technical Meeting of the Institute of Shaft Drilling Technology(ISDT). Las vegas NV, 1996: 1−10.

[20] ROSTAMI J, OZDEMIR L. A new model for performance prediction of hard rock TBMs[C]// Proceedings of the Rapid Excavation and Tunneling Conference. Boston, MA, 1993: 793−809.

[21] 屠昌锋. 盾构机盘形滚刀垂直力和侧向力预测模型研究[D]. 长沙: 中南大学机电工程学院, 2009: 23−36.TU Changfeng. Study of disc cutter’s vertical force and lateral force prediction model in shield machine[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2009: 23−36.

(编辑 杨幼平)

A wear prediction model of disc cutter for TBM

TAN Qing1, 2, SUN Xinjian1, 2, XIA Yimin1, 2, CAI Xiaohua1, 2, ZHU Zhenhuan1, ZHANG Jinhao1

(1. Key Laboratory of Modern Complex Equipment Design and Extreme Manufacturing, Central South University, Changsha 410083, China;2. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

In order to study the wear behavior of tunnel boring machine (TBM) disc cutters during the process of rock breaking, kinematic formulas of constant-section disc cutter were established through the analysis of motion characteristics between cutter head and disc cutter. The wear prediction model of disc cutter, which was programmed in MATLAB, was built by combining theory of abrasive wear and cutter-rock contact mechanics. The model was applied to simulate the wear process of cutters in a water diversion project. The evolution laws of wear morphology of disc cutters were obtained.The results show that the simulated wear quantity and the measured wear amount are consistent with the changing tendency of the tool position number, and the average relative errors of normal and lateral face wear of the disc cutters are 18% and 30%, respectively. The cutter ring gradually wears to be tip-shaped, which coincided with the actual wear form.

tunnel boring machine (TBM); disc cutter; wear prediction; numerical simulation

10.11817/j.issn.1672-7207.2017.01.008

TH117.1

A

1672−7207(2017)01−0054−07

2016−01−24；

2016−03−19

国家重点基础研究发展计划(973计划)项目(2013CB035401)；国家自然科学基金资助项目(51274252)；湖南省战略新兴产业重大科技攻关项目(2012GK4068) (Project(2013CB035401) supported by the National Basic Research Development Program (973 Program) of China; Project(51274252) supported by the National Natural Science Foundation of China; Project (2012GK4068) supported by the Major Science Projects of Hunan Province for Strategic Emerging Industry)

蔡小华，副教授，从事机械设计方法与理论、机械电子等研究；E-mail: 13607431291@139.com