并联双杆液压缸偏载力和径向力分析

訚耀保，李双路，陆畅，原佳阳，肖强

(1.同济大学机械与能源工程学院，上海，200092；2.中国航发长春控制科技有限公司，吉林长春，130102)

为了满足在有限空间内实现大推力的任务需要，航空发动机矢量控制系统及飞行器舵面控制系统空间布局和结构上需要采用一种双杆并联机械同步液压缸[1]，该液压缸缸体包含2 个缸筒，2根活塞杆通过连接块实现机械同步，通过缸体上的串联孔实现2个液压缸的油路连通。该结构实现了液压缸的扁平化设计，同时满足负载需求，但在实验中发现该液压缸尚存在如下问题：一是液压缸的导向套处和活塞上存在着不均匀磨损，二是活塞杆在运动到终点时存在抖动现象。上述问题影响到液压缸的运行寿命和可靠性，不利于伺服控制系统的安全。为了提高电液伺服系统的可靠性，保障飞行器飞行安全，需对液压缸的上述问题进行研究分析，降低液压缸的磨损和抖动。液压缸活塞杆运动到终点抖动问题是2根活塞杆的运动不同步造成的，在传统的双缸独立控制中，人们对该问题研究较多，可以通过各种控制策略提高2根活塞杆的同步性[2-5]；而液压缸承受的径向力会使导向套和活塞产生不均匀磨损[6]。研究表明，液压缸导向环上5%的磨损会使液压缸的承载能力降低约10%[7]。为了提高液压缸抗径向负载能力，静压支撑等非接触密封形式在液压缸中得到了广泛应用[8-11]；液压缸建模和运动过程中的载荷研究是优化液压元件、提高液压系统性能的基础，受到人们广泛关注[12-14]。本文作者针对并联双杆液压缸中的偏载力和径向力问题，建立液压缸的数学模型和超静定力学模型，探讨影响液压缸偏载力和径向力的关键结构参数，以便为优化该类型液压缸的结构、降低其工作中的径向力和偏载力、提高液压缸的适用性和可靠性提供依据。

1 并联双杆液压缸数学模型

1.1 并联双杆液压缸工作原理

图1所示为并联双杆液压缸的结构示意图。受限工作空间的限制，采用液压缸单侧供油，油液通过阀口和无杆腔的薄壁孔依次进入液压缸的上无杆腔和下无杆腔，推动活塞杆运动，下有杆腔的油液通过两缸之间的薄壁孔从上有杆腔回油，此结构减少了管路连接，工艺性好，集成度高，安装尺寸小。由于其结构和油路特点，并联双杆液压缸存在如下问题。

图1 并联双杆液压缸结构示意图Fig.1 Schematic diagram of parallel double rods hydraulic cylinder

1)受液压缸结构和工艺限制，两缸之间的串联孔个数和尺寸受到限制，串联孔的节流作用使得活塞杆在运动过程中2个无杆腔及有杆腔之间存在压差，从而使得2根活塞杆承受的负载力不一致而产生偏载；液压缸2根活塞杆在运动时不完全同步，在运动到终点时存在抖动现象。

2)由于连接块受到的外负载力与2根活塞杆对其的作用力不共线，会导致连接块和活塞杆发生变形，使得塞杆与导向套、活塞与缸筒之间存在很大的径向力，加剧了密封结构的不均匀磨损[15]。

1.2 并联双杆液压缸数学模型

根据并联液压缸的工作原理，不计液压阀和液压缸之间的压降以及液压缸的泄漏，当液压缸活塞杆伸出时，液压阀2个节流口的流量q1和q4表达式为：

上、下液压缸之间2个薄壁串联孔的流量q2和q3表达式为：

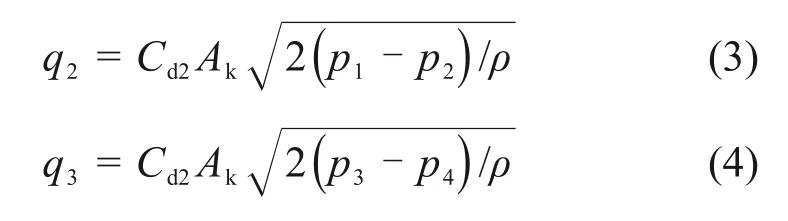
式中：ps为供油压力；p0为回油压力；p1，p2，p3和p4分别为容腔1～4 的压力；w为阀口面积梯度；xv为阀口开度；Cd1和Cd2分别为滑阀节流口流量系数和薄壁串联孔流量系数，为了便于计算偏载力，取两者相等，记为Cd；ρ为油液的密度；Ak为上下两缸之间串联孔通流面积。

容腔1～4的流量连续性方程分别为

式中：A1为活塞杆无杆腔面积；A2为活塞杆有杆腔面积；x为活塞杆运动速度。

忽略活塞杆运动时的摩擦力，根据牛顿运动定律，上下活塞杆及连接块的轴向受力平衡方程为

式中：F1和F2分别为活塞杆1和活塞杆2承受的负载力；FL为连接块承受的外负载。

同理可以得到活塞杆在缩回时的数学模型，采用数值求解方法研究并联双杆液压缸的偏载力和径向力，模型中的主要参数如表1所示。

表1 阀控液压缸数学模型主要参数Table 1 Main parameters of mathematical model of hydraulic cylinder controlled by valve

2 液压缸偏载力和径向力理论分析

2.1 液压缸偏载力

2.1.1 偏载力计算分析

如图1所示，定义外负载FL的作用线与连接块的质心交点为O点，由于2根活塞杆承受的负载力不一致会产生绕O点的偏载力矩，偏载力矩可用上下活塞杆承受的轴向负载力差值衡量，定义2根活塞杆的轴向负载力差值为偏载力ΔF，即

由式(5)～(8)可得：

由式(9),(10)和(12)可得：

结合式(6)，(7)和(13)可得活塞杆伸出时偏载力与阀口供油流量q1的关系：

式中：n为液压缸的不对称系数，n=A2/A1，n越小，表示不对称度越大。通过式(1)～(10)可以进一步得到无杆腔流量与外负载FL以及阀口开度xv的关系：

将式(16)代入式(15)可得当活塞杆伸出时偏载力ΔFs的表达式为

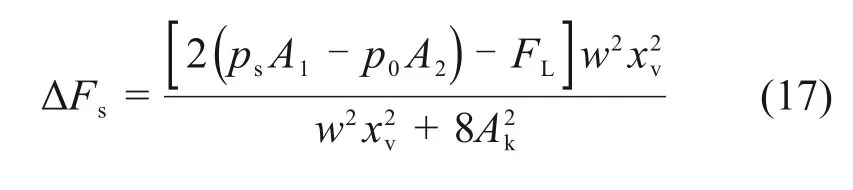
同理可得活塞杆处于缩回状态下的偏载力ΔFd表达式为

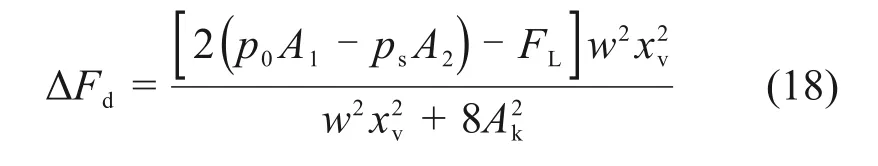
由式(17)和式(18)可以发现，增大串联孔的通流面积可以有效地降低偏载力。且由于阀口的通流面积远远小于串联孔的通流面积，式(18)分母中的第1项可以忽略，则偏载力和阀口开度近似呈二次函数关系。不同负载下偏载力随阀口开度的变换情况如图2所示。从图2可以看出：在同样负载下，阀口开度越大，偏载力越大；当阀口开度为正时，活塞杆伸出，上活塞杆承受的负载力更大；当阀口开度为负时，活塞杆缩回，此时，偏载力为负值，表明下活塞杆承受的负载力更大。

图2 不同阀口开度下的偏载力Fig.2 Offset load force under different valve openings

当阀口开度固定时，偏载力和外负载力的关系如图3所示。将外负载FL以最大额定负载Fmax为标准值进行无因次化，最小额定负载Fmin和最大额定负载Fmax计算式如下：

从图3 可以看出：偏载力和负载呈线性关系，在阀口开度为正时，随着负载力从最小额定负载逐渐增大，缸的流量减小，串联孔两侧的压差减小，偏载力逐渐减小；在阀口开度为负时，随着负载力从0 N逐渐增大，缸的流量逐渐增大，串联孔两侧的压差也逐渐增大，偏载力从0 N 逐渐增加。

2.1.2 偏载力对活塞杆运动顺序的影响

在液压缸启动时，偏载力会影响上下活塞杆运动的顺序。仅考虑上下活塞杆受到的液压力和最大静摩擦力，不安装连接块时，由液压缸的工作原理可知：

图3 不同负载作用下的偏载力Fig.3 Offset load force under different loads

1)由于油液先流入上液压缸，当下活塞杆运动时，上活塞杆受到的液压力始终大于下活塞杆受到的液压力，即F1＞F2。

2)当下活塞杆不运动时，上下两腔之间无压差，此时，上下活塞杆受到的液压力相同，即F1=F2。

若上活塞杆受到的液压力F1能够克服其受到最大静摩擦力Ff1，而下活塞杆受到的液压力F2小于其受到的最大静摩擦力Ff2时，上活塞杆会先运动，即

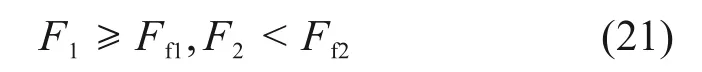
可得

定义上下活塞杆受到的最大静摩擦力之差Δf=Ff1-Ff2，则上活塞杆先运动的条件是

当下活塞杆受到的液压力F2能够克服其受到的最大静摩擦力Ff2而上活塞杆受到的液压力F1小于其受到的最大静摩擦力Ff1时，下活塞杆会先运动，即

因此，当下活塞杆先运动时，偏载力和最大静摩擦力之差需要满足的条件为

当上活塞杆受到的摩擦力小于下活塞杆的摩擦力即Ff1＜Ff2时，结合条件1)可知活塞杆的受力满足式(23)，上活塞杆先运动。由于上活塞运动后，其受到的滑动摩擦力比最大静摩擦力小，因此，上活塞杆将运动到底后下活塞杆才开始运动。

当Ff1≥Ff2时，若满足式(25)，则下活塞杆先开始运动，且由于运动后的滑动摩擦力小于最大静摩擦力，下活塞杆将运动到底后上活塞杆才开始运动；若不满足式(25)，假设此时上活塞杆先运动但下活塞杆还没运动，则由条件2)可知，此时F1=F2，由式(21)得Ff1＜F1=F2＜Ff2，与Ff1≥Ff2矛盾，故此时上下活塞杆将同时运动。

由上述分析可得上下活塞杆运动顺序发生变化的临界条件为ΔF=Δf，此时下活塞杆运动，而上活塞杆处于临界状态，有

结合式(1)，(2)，(3)，(4)和(12)可得引起下活塞杆先运动的无杆腔流量的临界值q1L与上下活塞杆摩擦力之差Δf的关系为

当下活塞杆伸出时，q1与阀口开度xv等存在如下关系，

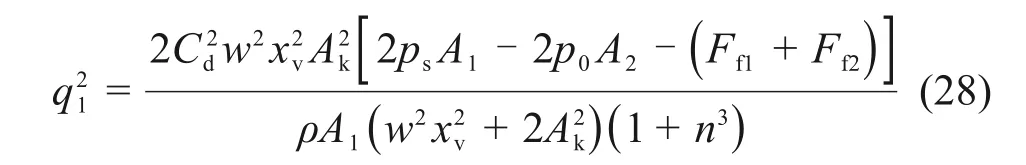
由此可得下活塞杆先运动时阀口开度的临界值xvL为

由于Ff1+Ff2和 Δf远小于 2psA1- 2p0A2，因此，式(29)可简化为

同理，活塞杆缩回时，可得引起下活塞杆先运动的临界阀口开度为

将表1 中参数代入式(30)和(31)可以发现：当最大静摩擦力相同时，活塞杆处于缩回状态时的临界阀口开度比活塞杆处于伸出时的临界阀口开度略大。无连接块时，若上活塞杆的最大静摩擦力大于下活塞杆最大静摩擦力，则当阀口开度大于临界值时，上下活塞杆同时运动；当阀口开度小于临界值时，下活塞杆先运动；而若上活塞杆的最大静摩擦力小于下活塞杆最大静摩擦力，则无论阀口开度大小，都是上活塞杆先运动。而当上下活塞杆被连接块连接时，2根活塞杆的先后运动会造成1个活塞杆通过连接块拖动另外1个活塞杆运动，考虑到2根活塞杆和缸筒以及导向套之间的配合间隙，当2个活塞端面先后与导向套接触时则会导致活塞杆抖动。产生这类抖动现象的原因正是由于偏载力与2根活塞杆受到的最大静摩擦力不匹配。

2.2 液压缸径向力

2.2.1 径向力简化计算模型

由于活塞杆匀速运动时受力平衡，当活塞杆和缸筒之间相对运动时，可视活塞杆静止，缸筒在活塞杆上滑动，因此，缸筒和活塞之间的约束关系可视为固定铰支座，活塞杆和导向套的约束关系可视为活动铰支座，可得到活塞杆受力简化模型如图4 所示。图4 中，FA，FB，FC和FD分别为上下活塞与缸筒及导向套之间的径向力；s为活塞杆端面至导向套外端面的距离，在活塞杆缩回时，s逐渐增大；l为液压缸活塞端面至连接块的距离；M为由于偏载产生的弯矩。

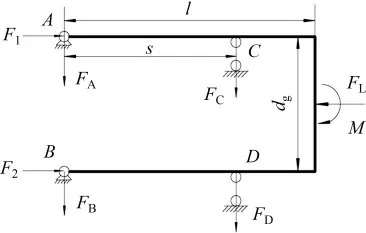
图4 活塞杆受力简化模型Fig.4 Simplified mechanics model of piston rods

该结构为三次超静定结构，可用力法求解各处内力[16]。由于该系统结构对称，在选取基本体系时可将杆件从对称轴处截断，进行对称处理，集中力FL和弯矩M分解为一对称力和反对称力的综合作用，原结构等效为如图5 所示的基本体系，且有

式中：dg为等效模型中连接块的长度；a为力矩等效作用在上活塞杆的力臂长度。

图5 等效受力模型基本体系Fig.5 Basic system of equivalent force model

对上述结构列变形协调方程：

式中：Xi(i=1,2,3)为原模型等效处理后的多余约束；δij(i,j=1,2,3)为当Xj为单位载荷时，Xi的作用点沿Xi方向上的位移；Δip为外载荷p在Xi的作用点，沿着Xi方向上的位移；δij和Δip可通过图乘法[16]得出，其中，活塞杆和连接块的惯性矩分别如下：

式中：d为活塞杆直径；h为连接块矩形截面高度；b为连接块厚度。

A和B点处于力矩平衡状态，对称结构的上下部分在水平和竖直方向上处于力平衡状态，则有

利用式(32)～(35)和图乘法可以联立求解出各位置的径向力。由图3 可知，当外负载为90 kN，阀口开度为-0.5 mm 时，此时，偏载力最大为-1.4 kN，结合图1 及表1 可得各径向力与活塞位置s的关系如图6所示。由图6可以发现：

1) 径 向 力FA与FB基 本 相 等 ，FC与FD基 本 相等，方向相反。活塞与缸筒之间的最大径向力FA和FB约为单活塞杆承受的轴向负载力(45 kN)的8%，活塞杆与导向套之间的最大径向力FC和FD最高时超过了轴向负载力的20%。

图6 活塞处于不同位置下的径向力Fig.6 Radial force of the piston at different positions

2)活塞杆在缩回过程中，活塞与缸筒之间的径向力逐渐减小，活塞杆与导向套之间的径向力先减小再增大，当活塞杆处于液压缸的中部位置附近时，径向力总体较小。由此可见，增加导向套的厚度可以减少活塞和缸筒之间的径向力，对于并联双杆液压缸，其工作行程不宜过长。

2.2.2 径向力影响因素分析

由于FA与FB基本相等，FC与FD基本相等，下面仅以FB和FC为例说明偏载力ΔF、连接块的厚度以及连接块材料对径向力的影响。

1)ΔF对径向力的影响。

分别求出在ΔF=0 N和ΔF=-1.4 kN时不同位置状态下的径向力。偏载力对径向力的影响见图7。由图7 可见：当活塞杆负载差值从-1.4 kN 变化到0 N时，径向力几乎没有发生任何变化，因此，减小偏载力对降低径向力没有明显作用。

图7 偏载力对径向力的影响Fig.7 Effect of offset load force on radial force

2)连接块厚度对径向力的影响。

图8所示为连接块材料为钛合金，厚度分别为20，30 和40 mm 时，活塞杆处于不同位置下的径向力。由图8可见：连接块厚度对径向力的影响显著，当连接块厚度增加到40 mm 时，缸筒和活塞之间的径向力下降到轴向力的2%以下，而活塞杆和导向套之间的径向力下降到轴向力的7%以下。

图8 连接块厚度对径向力的影响Fig.8 Effect of connecting block thickness on radial force

3)连接块材料对径向力的影响。

图9所示为当连接块厚度为20 mm，材料为钛合金以及不锈钢时，不同位置下的径向力。由图9可见：通过使用体积弹性模量大的材料可以有效降低活塞和缸筒以及活塞杆和导向套之间的径向力。

图9 连接块材料对径向力的影响Fig.9 Effect of connecting block material on radial force

2.2.3 径向力有限元计算

液压缸受到的径向力亦可以通过有限元仿真进行计算。液压缸径向力仿真设置如图10 所示。缸筒铰链连接处设置为固定约束，通过分析可知，径向力主要由结构所致，与上下活塞杆的轴向偏载力关系不大，因此，在连接块的轴端轴承组件施加90 kN 的外负载，2 根活塞处均施加45 kN 的轴向载荷。为了加快仿真收敛，除活塞与缸筒、导向套与活塞杆之间设置为摩擦因数为0.001的有摩擦约束外，其余配合约束皆为固定约束。

图10 液压缸径向力仿真设置Fig.10 Hydraulic cylinder radial force simulation settings

径向力简化模型和仿真结果对比如图11所示。由图11 可以发现：仿真计算得到的导向套与活塞杆处的径向力FC比简化模型计算结果更大，而活塞与缸筒之间的径向力FB的仿真结果与简化模型计算结果非常接近。两者的误差是由于简化模型忽略了诸多细节因素，模型中物理量的选取也难以完全反映实际，但活塞杆在不同位置下的简化模型计算结果和仿真结果显示了相同的变化趋势，说明该简化模型可以为工程设计提供参考。

图11 径向力简化模型和仿真结果对比Fig.11 Comparison between simplified model result and simulation result of radial force

3 活塞杆运动理论结果与实验结果对比分析

液压缸实验原理图见图12。在系统供油压力为5 MPa时，使用RP3燃油作为传动介质，分别进行不同阀信号电流下液压缸在有、无连接块下的实验，实验所用伺服阀为某型射流管伺服阀，采用自研液压缸，缸筒材料为钛合金，活塞杆材料为不锈钢，主要结构参数见表1。当不安装连接块，控制阀信号电流小于6 mA时，下活塞杆先伸出到底，上活塞杆再伸出；当信号反向时，下活塞杆先缩回到底，上活塞杆再运动；当阀信号电流分别为7，15 和40 mA 时，上下活塞杆同时运动；当安装上连接块后，阀信号电流较小时，可以观测到活塞杆在伸出到底时有轻微的抖动现象；当信号电流较大时，抖动现象比较明显。取下连接块并重新调整安装活塞杆后，再在供油压力5 MPa 下进行实验，发现当阀信号电流分别为5，7，15 和40 mA 时，上下活塞杆均同时启动。调整安装之后的实验现场如图13所示。

图12 液压缸实验原理图Fig.12 Experimental schematic diagram of hydraulic cylinder

图13 活塞杆动作同步实验Fig.13 Synchronization experiment of piston rods

上述实验结果表明：在取下活塞杆重新安装之前，上活塞杆受到的最大静摩擦力更大，且上下活塞杆的最大静摩擦力相差较大，因此，当阀信号电流较小时，下活塞杆先运动；当阀信号电流增大到一定值时，才能使上下活塞杆同时运动；重新装配后，上下活塞杆受到的最大静摩擦力的差异减小，但上活塞杆的最大静摩擦力仍然比下活塞杆受到的最大静摩擦力略大，因此，在5 mA的小信号电流下仍然是上下活塞杆同时运动，该实验现象与本文第2.1.2 节中偏载力对活塞杆运动顺序的影响的理论分析结果基本一致。

4 结论

1)推导出液压缸上下活塞杆承受的偏载力表达式。当负载力一定时，偏载力近似为阀口开度的二次函数；当阀口开度一定时，偏载力与负载力呈线性关系。活塞杆伸出时负载越大，偏载力越大；当活塞杆缩回时，负载越大，偏载力越小。增大串联孔孔径可以有效降低偏载力。

2)活塞杆运动到终点产生抖动现象的原因是上下活塞杆的偏载力与受到的最大静摩擦力不匹配。当上活塞杆的最大静摩擦力小时，总是上活塞杆先动作，而当下活塞杆的最大静摩擦力小且阀口开度低于临界开度时，则下活塞杆先动作。安装连接块后，上下活塞杆运动不一致会导致活塞杆在运动终点产生抖动现象。

3)随着活塞杆的伸出，活塞与缸筒之间的径向力逐渐增大，而活塞杆与导向套之间的径向力先减小再增大。通过增加连接块的厚度以及采用弹性模量更大的材料可以使径向力得到有效减小，径向力与液压缸的偏载力关系不大。