数控周边磨床主轴系统热关键点选取及热误差建模

廖启豪，王玲，殷国富，谢政峰

(四川大学机械工程学院，四川成都，610065)

热误差是机床误差的主要来源之一，由温度引起的误差可以占到机床总几何误差的75%[1]。减少热误差的途径主要包括热误差防止、热误差控制和热误差补偿3种方法，与前2种方法相比，热误差补偿更易实现且成本更低[2]。热误差补偿主要通过建立热误差模型实现，热误差建模依赖于热关键点的温度，因此，热关键点选取和热误差建模是热误差补偿的主要研究内容。马驰等[3-4]通过模糊聚类和灰色聚类方法选取热关键点，并通过遗传算法和粒子群算法寻找合适参数建立了基于BP 神经网络的热误差模型；谭峰等[5-6]通过模糊C均值聚类选取热关键点，并基于集成BP神经网络和最小二乘支持向量机建立了主轴热误差模型；周宝仓等[7]通过模糊聚类和相关系数确定热关键点，建立了基于最小二乘方法的热误差模型；张捷等[8]通过模糊聚类和灰色关联度方法选取了热关键点，建立了基于遗传算法径向基函数神经网络的高速电主轴热误差预测模型；DU 等[9]从相关性的角度出发，选取了与热误差相关系数最大的点作为热关键点；LIU等[10]采用模糊聚类和灰色关联度结合的方法选取热关键点，并采用岭回归算法建立热误差模型。上述建模方法在对温度测点分类之后多采用相关系数和灰色关联度方法在每一类中选取热关键点。已有研究[11-12]表明，根据温度与热误差之间的关系所确定的热关键点是动态变化的，即机床在不同运行状态下确定的热关键点不完全一致。为此，本文作者提出一种基于时间特性的热关键点选取方法，在选点过程中只依赖于温度测点的温度；针对数控周边磨床主轴系统，实施不同运行状态下的热误差实验，并从16 个温度测点中选取3个温度测点作为热关键点；利用多元线性回归、BP 神经网络、支持向量机等方法建立热误差模型，以验证本文热关键点选取方法的有效性。

1 热关键点选取方法

热关键点是指在机床热误差建模过程中其温度变化对热误差有决定性影响的温度测量点[2]。热关键点的选取一般包括分类和选择，即先将所有的温度测量点分为几类，再从每一类中选取特定的点作为热关键点。通过比较温度与热误差之间的相关性来选择同一类中的热关键点，是一种常见的选点策略。但是，对于机床主轴系统来说，使用不同转速图谱下的温度和热误差得到的热关键点是不恒定的[12]。特定转速图谱下得到的热关键点在用于预测该转速图谱的热误差时能保证一定的精度，但当用于其他转速图谱下的热误差预测时，不能保证有良好的泛化性能。

基于相关性的热关键点选取方法强调了温度与热误差的相关关系，却忽略了其因果性。主轴系统的轴向伸长量取决于流入和流出的热量，前后轴承是主轴系统最主要的热源，由此可以得到主轴轴向热变形的初步理论模型[13]为

式中：δ为轴向热变形；Tfec为前端面温度；Tfb为前轴承温度；Te为环境温度；αt为待定参数；L为伸出端长度。

上述参数中，前轴承温度Tfb代表了热源温度，符合热关键点的温度要求。但对于主轴系统而言，直接测量热源温度需要破坏主轴箱结构，选择主轴箱外表面靠近热源的点作为热关键点是可行的方式之一。已有的研究表明，越靠近热源的点，在整个热误差实验过程中相对于其他温度测量点其温度最先达到最大值[9]。基于这种时间特性，本文作者提出1 种热关键点的选取方法，其表达式如下：

式中：xij为第i个温度测量点在第j分钟的温度；α(i)为第i个温度测点达到最大温度时对应的时间；β(i)为α(i)归一化处理后的结果；m为温度测量点的总个数；n为实验总的测量时间。β(i)越小，即表示该点在整个温度测量过程中越先达到最高温度，越适合作为热关键点。

2 主轴系统热误差实验

在某型号数控周边磨床上布置温度传感器和热误差传感器进行热误差实验。使用PT100磁吸式温度传感器采集主轴系统外表面15 个点的温度以及距主轴箱一定距离的环境温度；同时，非接触式激光位移传感器通过夹具固定在床身立柱上，用于测量主轴轴向热位移。温度传感器每分钟采集1次全部测点的温度并保存在数据采集器中，激光位移传感器采样频率为1.5 kHz，取每分钟全部测量值的平均值作为该时刻的位移并保存在计算机中。

主轴系统表面温度传感器布置如图1所示。其中1号传感器和4号传感器分别位于主轴箱表面靠近主轴前后轴承处；2 号和3 号传感器均布于1 号和4 号传感器之间；5 号、6 号、7 号和8 号传感器分别位于1号、2号、3号和4号传感器下方主轴箱表面凹槽处；9号传感器位于主轴箱与前端盖连接处，靠近前轴承；10号、11号、12号和13号传感器布置于主轴箱与底座螺栓连接处；14 号和15 号传感器位于主轴电机与主轴箱连接法兰两端；16号传感器置于距离主轴箱一定距离处，用于测量环境温度。

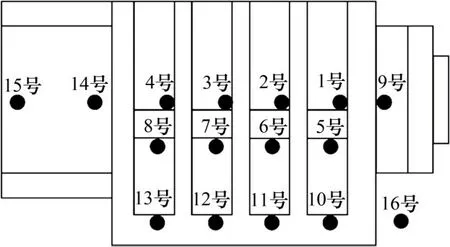
图1 主轴系统表面温度传感器布置Fig.1 Temperature sensors arrangement of spindle system surface

热误差实验分别在3种转速图谱下进行。转速图谱A 和转速图谱B 为GB/T 17421.3—2009[14]推荐的变转速图谱，分3 次连续运转，总运行时间共240 min，每次连续运转之间暂停15 min，共暂停30 min，运行完成后停机冷却90 min。其中，转速图谱A的最大转速为3×103r/min，转速图谱B的最大转速为2×103r/min。变转速图谱是为了模拟机床主轴在不同转速下的运行情况而设置的，其转速分布如图2 所示。转速图谱C 为恒定转速2×103r/min，运行时间为240 min，运行完成后停机冷却90 min。

图2 变转速图谱Fig.2 Variable speed spectrum

通过热误差实验得到3种转速图谱下的轴向热误差分布，如图3所示。其中，转速图谱C对应的主轴最大热误差最大，转速图谱B对应的主轴最大热误差最小，这与“转速越大，热生成量越大，热误差越大”的客观规律相符。由图3 还可以看出：在主轴按变转速图谱运行时，3次连续运转之间的2次暂停均使轴向热误差明显减少，说明主轴停转以后，由于热源不再生热，剩余的热量不足以维持主轴热膨胀继续。

转速图谱A对应的温度测点的温度分布如图4所示(为便于显示，图4 中只展示了偶数号测点的温度变化)。由图4可以看出：温度最高的3个测点分别为4 号、14 号、8 号，这3 个测点都位于后轴承附近。温度最低的测点为16 号测点，该测点测量的是距离主轴系统有一定距离的环境温度。由此可见，随着主轴运转，距主轴系统较近距离的环境温度也随之变化，说明主轴箱外表面热边界条件处于动态变化之中。

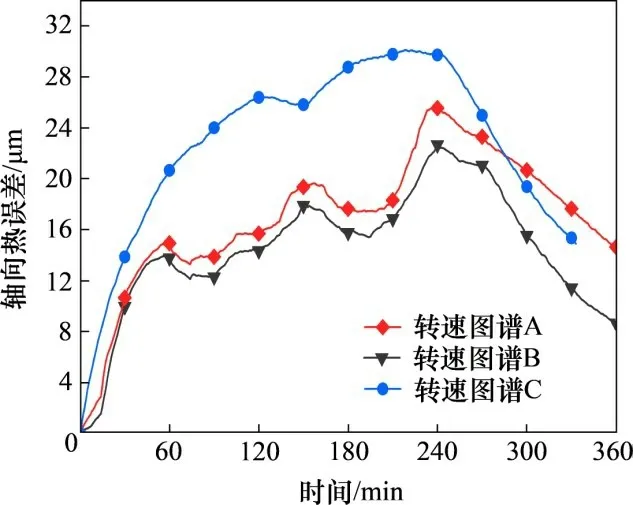
图3 主轴轴向热误差分布Fig.3 Axial thermal error distribution of spindle

图4 变转速图谱A对应的温度分布Fig.4 Temperature distribution of variable speed spectrum A

3 热误差建模过程与结果

3.1 温度测点分类

用于热误差建模的热关键点的数目不宜过多。一方面，一些无关数据的引入可能影响建模精度；另一方面，实际应用时，机床表面也不可能布置大量传感器[2]。按照先分类后选取的原则，需要对16个温度测点进行分类。模糊C均值聚类[15]是一种无监督的聚类方法，通过指定聚类数和模糊权重指数，计算模糊目标函数。

模糊目标函数可以表示为

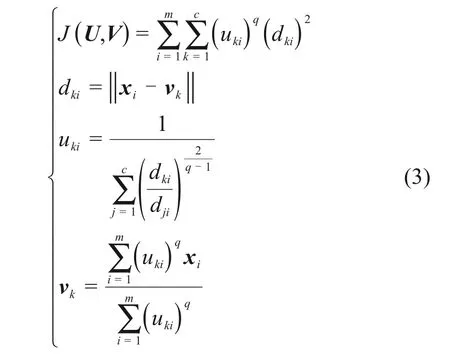
式中：J为模糊目标函数；c为分类数；q为权重指数；xi为由第i个温度测量点的温度数据组成的温度向量；vk为第k个类的聚类中心；uki为第i个温度测量点对第k个类的隶属度；dki为温度向量xi与第k个类的聚类中心vk的距离。

计算时，先初始化隶属度矩阵U，然后求得聚类中心V，再计算隶属度矩阵U，最后计算目标函数J。循环迭代，直到隶属度变化量满足给定值或达到最大迭代次数时为止。模糊C均值聚类的分类数需要事先给定，分类数即是热关键点数目。考虑到前后轴承作为主要热源以及其他热源可能带来的影响，同时为了尽量减少热关键点数目，对于周边磨床主轴系统选取热关键点数为3个。将变转速图谱A对应的16个温度测点的温度代入计算，取权重指数为2，隶属度最小变化量为1×10-5，最大迭代数为300次，得到的温度测点分类结果如表1所示。

表1 分类结果Table 1 Classification results

3.2 热关键点选取

为验证本文所述热误差关键点选取方法的有效性，选择基于皮尔逊相关系数[7]的方法和基于灰色关联度[8]的方法作为对比。

皮尔逊相关系数pi可以表示为

式中：yj为主轴第j分钟的轴向热误差；为第i个温度测量点的平均温度；为轴向热误差平均值。

同样地，灰色关联度gi可以表示为

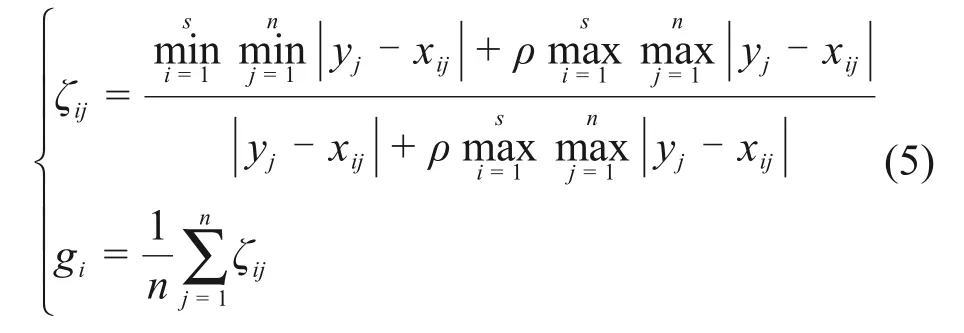
式中：s为温度测点的数目；ρ为分辨系数，通常取0.5；ζij为关联系数。

分别使用皮尔逊相关系数、灰色关联度和式(2)中基于时间特性的排序方法对转速图谱A 得到的16 个温度测量点进行计算，按计算得到的温度从小到大排序，其排序结果如表2所示。由表2可以看出：皮尔逊相关系数和灰色关联度的排序结果相似，因为2种方法都是以温度和热误差的相关程度作为计算的依据。

表2 不同方法的计算结果Table 2 Calculation results of different methods

结合表1的分类结果和表2的排序结果，在每一类中选取排序靠前的点作为热关键点。当选取3个点作为热关键点时，可以得到基于皮尔逊相关系数和灰色关联度以及时间特性3种方法下的选点情况，如图5所示。值得注意的是，基于灰色关联度的方法和基于皮尔逊相关系数的方法在表2的排序结果中相似，在选点结果上完全相同。

图5 不同方法下热关键点选取结果Fig.5 Thermal key points selection results of different methods

从图5 可以看出：基于时间特性的选点方法(方法1)选取了代表前后轴承(9 号和4 号)和环境温度(16号)的点，基本符合热交换规律。基于相关系数的选点方法(方法2)选取了前后轴承之间(2号和3号)以及螺栓结合部(12 号)的温度测点。已有研究表明，靠近结合部的部分由于固定约束的存在，对总热误差的贡献很小[16]；同时，环境温度的变化是影响热误差的因素之一[17]。因此，从选点结果上看，基于时间特性的选点方法更符合主轴系统实际情况。

3.3 热误差建模

为证明基于时间特性的选点方法的有效性，分别选择支持向量机(SVM)、多元线性回归(MLR)以及BP神经网络(BPNN)这3种建模方法，利用已确定的热关键点进行热误差建模。

3.3.1 支持向量机

支持向量机在热误差建模中具有较高精度和较好的鲁棒性，其回归模型[18]可以表示为

选择高斯径向基核函数K(Xk,X)=作为回归模型核函数。其中，σ为宽度参数，记1/σ2为g。支持向量机回归模型由参数C和g确定，本文采用交叉验证法从2-4～24范围内寻找合适参数。

3.3.2 多元线性回归

多元线性回归模型可以表示为

式 中 ：β=(β0,β1,…,βp)，为 待 确 定 的 系 数 ；x1,x2,…,xp为p个热关键点的温度。

待定系数的求解可以通过最小二乘法计算，其表达式如下：

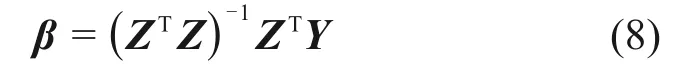
式中：Z为元素全为1的列向量和热关键点温度向量构成的矩阵；Y为对应热误差构成的列向量。

3.3.3 BP神经网络

BP 神经网络包含输入层、隐含层和输出层，简单的BP 神经网络隐含层只有1 层，各层节点的数目由实际需求决定。对于热误差建模而言，输出层节点为1，输入层节点数即为热关键点数，隐含层节点数根据建模效果来确定。本文利用Matlab神经网络工具箱建立输入层节点数为3、隐含层节点数为6、输出层节点数为1 的BP 神经网络，隐含层函数为logsig，输出层函数为purelin，学习速率为0.05，最大训练次数为3×103。

3.4 预测结果与精度评价

为评价建模精度，选择热误差实测值与预测值之间的均方根误差(RMSE)作为评价指标。以转速图谱A 下获得的热误差和热关键点温度作为训练集训练3 种模型，再分别利用转速图谱A，B 和C下的热关键点温度对热误差进行预测，对应的预测集分别为A1，B1和C1。由于BP 神经网络的初始权值和阈值是随机给定的，因此，每1次预测的结果都不完全相同，取10 次预测的平均值作为建模精度的结果。图6所示为支持向量机模型用2种选点方法对转速图谱A 下的热误差的预测结果和建模误差。2 种选点结果对应的3 种建模方法共9 组18 次预测的精度(以 RMSE 表示，RMSE 越小，精度越高)如表3所示。

从表3 可以看出：基于时间特性的选点方法(方法1)对3种建模方法的建模精度都有所提高。3种模型的9组预测中，均方根误差降幅最低为6%，最高为40%。在3 种建模方法中，BP 神经网络模型在自预测(训练集和预测集相同)时精度最高，交叉预测(训练集和预测集不同)时精度最低。与其他2 种建模方法相比，多元线性回归模型(MRL)在自预测时精度最低，而支持向量机模型在自预测和交叉预测时都能保证较高的预测精度，显示了其在热误差建模方面的鲁棒性和良好的泛化性能。

图6 不同选点方法的建模结果Fig.6 Modeling results of different points selection methods

表3 不同选点方法建模精度Table 3 Modeling accuracy of different points selection methods

2种选点方法在建模精度上产生差异的原因在于：基于相关系数的方法依赖于单次实验的数据，忽略了不同转速图谱下的热误差实验产生不同的热关键点所带来的影响。同时，从图5 可以看出，靠近主轴前轴承的点其温度变化不大。在实验过程中，主轴前端法兰结构转动所引起的空气流动对主轴前端的温度测点产生了降温的效果，这将改变主轴箱外表面热边界条件，从而影响基于相关系数的选点结果。

4 结论

1)提出一种基于时间特性的热关键点选取方法，该方法与基于相关系数和灰色关联度的方法相比，减少了模型的不稳定性，避免了由于主轴系统运行状态变化对热误差关键点选取的影响。

2)针对某型号数控周边磨床主轴系统，设计并实施了热误差实验；使用3种选点方法，分别从16个温度测点中选取了3个点作为热关键点。

3)利用支持向量机、多元线性回归以及BP神经网络3种建模方法进行热误差建模，采用本文方法选取热关键点，其热误差实测值与预测值之间的均方根误差降幅最低为6%，最高为40%，证明了本文热关键点选取方法的有效性。