一种基于互斥平衡原理的圆度测量方法
任晟德,玉振明,李陶深, 韦衡冰
(1.广西大学 计算机与电子信息学院,南宁 530004;2.梧州学院 图像处理与智能控制重点实验室,广西 梧州 543000)
一种基于互斥平衡原理的圆度测量方法
任晟德1,玉振明2,李陶深1, 韦衡冰2
(1.广西大学 计算机与电子信息学院,南宁 530004;2.梧州学院 图像处理与智能控制重点实验室,广西 梧州 543000)
提出一种新的基于数字图像处理的圆度测量方法。通过引入物理学的互斥力概念,以线性迭代的方式基于圆环像素群综合斥力移动准圆心点,并附加像素群角度修正,使其停止在受圆环像素群综合受力为零的点,该点即为文中方法所求圆心点。理论分析和实验验证了使用此方法获取的圆心点及零件圆度均与传统非接触测量测量结果相近,可应用于实际的圆度测量工作,也为未来的圆度测量研究提供一种新思路和新方法。
图像处理;圆度测量;互斥平衡
0 引言
圆度误差是机械零部件经常检测的项目之一,随着现代工业逐渐朝着高精度、高速度、自动化的方向发展,传统的接触测量方法由于其人工操作速度较慢、精度不够稳定、可能产生划痕等缺点,渐渐很难满足现代工业需求[1]。近年来,随着数字图像处理技术的不断发展,基于数字图像的在线检测技术也开始逐渐地应用于工业自动化生产中来,图像测量技术凭借着其非接触、实时、操作方便、信息量丰富等诸多优点,在工业测量领域发挥着日益重要的作用,有着广阔的应用前景[2]。
目前较为常用的基于数字图像的圆度误差评定方法主要有四种,即最小二乘法,最小区域法,最大内接圆法和最小外切圆法[3]。其中最小二乘法是这四种方法中使用最普遍的一种,其理论已较为成熟,精度也仅在最小区域法之下[4]。除此之外还有许多新的圆度测量方法,如使用遗传算法[5]、神经网络[6]、粒子群优化算法[7]、区域搜索[8]等方法进行的圆度测量方法。
本文结合已有的数字图像圆度测量理念,提出了一种新的圆度测量方法。通过引入物理学中的互斥力概念,将求解圆度的问题转化为依据圆环像素群的综合行为向圆心迭代的问题。解决方法为预先在圆内任意放置一个准圆心点,使准圆心点受到来自圆环像素群的综合斥力,准圆心点即会依据此斥力的方向和大小朝着互斥平衡点移动,通过不停的迭代移动,准圆心点最终会在圆环像素群的综合影响下停止于圆的互斥平衡点,该点即为本方法所求圆心点。
1 构建模型
1.1 原理简介
假设有一个标准圆,圆环由同质量同带电荷量且固定不动的标准正电子组成。这时,在圆环中任意位置放置一个自由正电子,圆环内部的正电子即会受到来自圆环上各处正电子的斥力,位于圆环内部的自由正电子即会在各个排斥力的综合作用下开始运动,最终停止在一个受到互斥力互相平衡的地点,对于一个标准圆来说,停止的点,也就是受到的互斥力平衡的点,即为圆心所在的位置。
在非标准圆的情况下,假定此非标准圆由一个标准圆开始形变,则当其边缘向圆内移动时,其理论圆心也将向圆的另一侧移动,其互斥平衡点也同样朝着圆的另一侧移动,反之亦然。由以上两点可知,非标准圆的互斥平衡点与理论最小圆度的圆心位置两者有着相似的分布特性。
通过大量的实验证明,在各种标准及非标准圆中,所求的互斥平衡点均与使圆度最小的理论圆心点极为相近。在第二部分的实验中也使用本方法对实际零件进行测量,有着令人满意的结果。
1.2 构建模型
对于物理模型而言,受到综合斥力公式为:∑Fij(斥力Fij的向量和)。
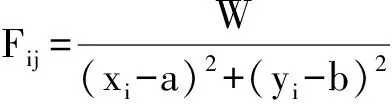
结合力的方向,可将单点的互斥力表示为向量形式,即:
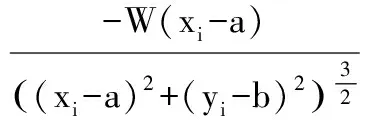
则准圆心点受到的圆环像素群给予的综合斥力为:
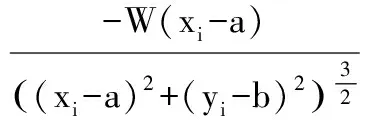
算法的最终目标是要求得互斥力平衡时的准圆心位置,即使综合斥力为零时的准圆心点像素a,b。
在物理层面求取该圆心点时,使用的方法是将一个自由电子放在圆内的任一位置上,自由电子在互斥力的作用下开始移动,最终停止在互斥平衡点。电子在圆内的移动轨迹由当前的速度方向和时时变化的互斥力综合决定,这是个非线性问题,描绘其移动轨迹的难度不下于从三维层面求解圆度。
将问题转换到图像中时,对非线性问题的求解通常使用线性迭代的方式。在使用线性迭代的方法简化问题时,可以使得准圆心在受到互斥力后,依据当时的受力大小和方向来移动相应的距离,这个移动是线性的。在到达下一个点后,再计算受力大小和方向来移动相应距离,迭代数次直到移动的像素数低于阈值,即可以通过准圆心受力后的线性移动来迭代求解出互斥平衡点的位置。
将综合受力在水平(x),竖直(y)轴上进行分解,可得:
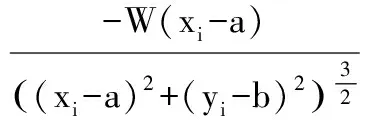
对分解的综合受力附加移动权值(k),下一个准圆心点(Xn+1,Yn+1)的坐标为:
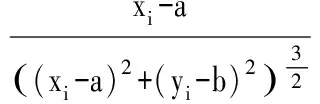
对上两步进行迭代,直到x,y方向上移动的像素均小于阈值,即可求得互斥平衡点的位置,也就是本方法所求得的圆心位置。
1.3 模型优化
考虑一个特殊的情况,假定处理的非标准圆只是一个半圆,那么在半圆中放置的任何一个准圆心,都会在迭代后通过半圆的开口无限远离半圆,即不存在任何的受力平衡点,也就没有办法求取圆心。
即便不考虑这样的特殊情况,在大多数的非标准圆中,边缘像素的分布也不可能是完美均匀分布的,在这样的情况下进行互斥力迭代,最终会收敛到边缘像素较少的一边。由于圆度测量结果不考虑边缘像素的多少,这样由于边缘像素分布不均匀带来的圆度误差是我们不能接受的。
由上面的问题分析可知,问题出在当准圆心进行综合受力时,力的方向并不是均匀的,即不考虑距离也就是力的大小时,准圆心受到的来自各像素的标准力叠加后,仍然有偏向性,也即是说偏向方向没有像素可以给予准圆心互斥力,使得准圆心朝着偏向方向移动。
偏向向量在x,y方向上分解后的大小为:

本文采用了一种较为简单的解决办法,既然问题出在偏向方向上没有像素可以给予准圆心互斥力,那么就可以通过在偏向方向附加相应数量的像素来解决该问题。
这样,全部的基于互斥平衡求取圆度的方法就完成了,求解流程如下:
①随机在圆内的位置放置一个准圆心点;
②计算准圆心点受到的综合斥力,结合权值将其在x,y方向上进行分解;
③计算准圆心点的偏向方向和大小,结合半径求取附加像素的斥力大小;
④结合②、③步的综合受力,附加权值,移动准圆心点;
⑤将第②、③、④步迭代数次,直至移动像素小于阈值,此时准圆心点的位置即为圆心所在的位置。
2 实验与结果分析
实验采用将本方法与传统的接触式测量方法进行比较的方式,通过实验室的测量系统结合本方法对实际零件进行圆度测量,并将结果与通过千分尺进行的传统接触式测量结果进行比较分析。
2.1 实验构建
2.1.1 图像采集与摄像机标定
实验使用实验室图像测量系统,由一个已标定好的工业CCD摄像机与相关的支撑部件组成。
本实验采用的CCD摄像机型号为维视图像EM-120M,是较常用的工业摄像机的一种,在各种工业测量上都有着较高的精度。分辨率则与成本息息相关,实验中使用的相机分辨率为1280×960,采集的图像如图1所示。

图1 采集到的原始图像
摄像机在测量之前由标准标定板进行标定,并根据标定数据调整摄像机位置,当相机与零件表面垂直时(即当其旋转矩阵R接近单位阵),固定摄像机位置。
算法求得的零件半径及圆度以像素为单位进行表示,使用之前标定中求得的摄像机矩阵P即可将像素距离转化为实际距离,在本次实验中,像素数与物长(单位:mm)之比为0.0596,即一像素距离代表0.0596mm。
2.1.2 边缘检测
受CCD相机特性及光学衍射效应的影响,零件的边缘是一个渐变的过渡区域[9]。要求取亚像素级别的图像边缘,首先采用传统的边缘检测算子如canny,sobel算子进行像素级的粗定位,再在已定位的边缘附近依据其灰度分布,通过插值法、拟合法及矩方法进行亚像素级别的精定位[10]。
本实验采取Canny边缘检测算法提取整数级的边缘图像,再使用双线性插值的方法求取亚像素级边缘点。
2.1.3 实验参数分析
在进行实验时,需要对两个值进行预设,一个是随机放入圆内的初始准圆心点位置,一个是迭代优化中的权值,本实验通过以下方式对这两个值进行初设。
(1)初始准圆心点。准圆心点的取值不对最终的处理结果造成影响,因为任何在圆内取得的准圆心点,都会在互斥力的作用下移动到圆的互斥平衡点,该互斥平衡点是不受初始点的影响的。本实验采用先随机在图像内取值再加以验证的方法,由于圆外点移动的方向和大小变化较小,而圆内点移动的方向和大小变化情况更为突出,即可依据其前三次的迭代移动大小和方向确定初始准圆心点是否在圆内。
(2)权值。权值的取值决定了准圆心点是否可以迭代收敛到互斥平衡点,和收敛的速度,我们通过理论分析可知,当权值大于一定的值,准圆心点会在互斥平衡点两边来回移动,甚至会移出圆,而较小的权值仅会使迭代次数变多,对实验结果造成较小影响。通过实验证明,对于闭合图像宽、高度均在图像宽、高度的1/2以上的情形下,可取权值为-(图像宽+高),负值代表斥力。
2.2 结果分析
使用千分尺对圆形零件进行接触式测量实验,获得表1结果,测量得平均半径为21.487mm,在已测结果中圆度为0.105mm。

表1 千分尺测量结果
使用本文方法进行非接触圆度测量实验,在圆内靠边缘位置选取四个初始圆心点,初点为(600,400)的算法迭代过程由图2所示,测量结果如表2所示。

图2 迭代轨迹

序号初点坐标权值终点坐标迭代次数圆度(pix)1(600,400)-1120(486.98,647.305)1082.6222(600,400)-2240(486.876,647,541)532.473(600,400)-3360(486.895,647,486)422.5074(400,400)-2240(486.845,647.376)442.4815(600,880)-2240(486.846,647.441)302.4546(600,880)-2240(486.888,647.519)482.496
由上述实验结果可知,本方法求取的零件平均半径转化到实际距离为21.456mm,与实际测量的平均半径相比误差小于0.03mm,相较于零件半径误差小于0.2%;本方法求取的圆度在误差最大时为0.156mm,由于实际测量的圆度会由于未测量到极大极小点而略小于实际圆度,故而本方法求取的圆度相较于实际圆度误差小于0.05mm,相较于零件半径,误差小于0.3%。
在时间复杂度方面,当半径增大时,相应增加权值即可减少迭代次数,可使得迭代次数始终收敛在一个范围内。因此本方法的时间复杂度仅与边缘像素数有关,为O(n),n为边缘像素数,适用于半径像素较大的图像。且其测量时间为毫秒级,适用于实际的测量工作。
由以上实验结果可知,本文所构想的通过物理学的互斥平衡理念求取圆度的方法在实验中证明了其可行性,与传统的接触式测量相比也有着较高的精度和速度,有着不错的实际应用价值。
3 结束语
本文通过引入物理学的互斥概念,将求解圆度的问题转换为圆环像素群的综合行为,并证明了互斥平衡点点与理论圆心相一致,提供了一种新的求解圆度的方法。并且在本文方法的基础上,可以通过在迭代中优化圆环像素群的方式求取其圆度最小的理论圆心,为未来的圆度测量研究提供一个新思路。
[1] 赵秀锦,侯学晖.图像处理在零件检测中的应用[J].微计算机信息,2008,24(8) :306-307.
[2] 陈向伟,王龙山,刘庆民.图像技术在微小零件几何尺寸测量中的应用[J].工具技术,2005,39( 8) :86-89.
[3] 董兆鹏,黄富贵.圆度误差测量及评定方法综述[J].工具技术,2011,45(2) :14-19.
[4] 余文咏,朱世根,骆祎岚,等.基于图像处理技术的零件圆度评定研究[J].组合机床与自动化加工技术,2015(7):74-76.
[5] Cui Changcai, Che Rensheng, et al. Circularity error evaluation using genetic algorithm[J] . Prec. Eng. , 2001, 9(6): 499-505.
[6] 葛动元, 姚锡凡, 向文江. BP 神经网络在麻花钻圆度误差检测中的应用研究[J] .武汉科技大学报, 2009, 32(4): 413-417.
[7] 崔长彩, 黄富贵, 张认成,等.粒子群优化算法及其在圆度误差评定中的应用[J] . 计量学报, 2006, 27(4): 317-319.
[8] 黄富贵, 郑育军.基于区域搜索的圆度误差评定方法[J].计量学报, 2008, 29(2): 117-119.
[9] 吴晓波.图像边缘特征分析[J].光学精密工程,1999,7(1):59-62.
[10] 孙少红,袁华,张彤.常用的亚像素边缘检测方法的对比研究[J].大众科技,2014,16(4):27-29.
(编辑 李秀敏)
A Method of Measuring Roundness Based on the Mutex Balance
REN Sheng-de1,YU Zhen-ming2,LI Tao-shen1,WEI Heng-bing2
(1. College of Computer,Electronics and Information, Guangxi University, Nanning 530004, China;2. laboratory of image processing and intelligent control, Wuzhou University, Wuzhou Guangxi 543000, China)
This paper puts forward a new method of roundness measurement based on digital image processing techniques. The concept of mutex balance in physics is introduced in the proposed method. In the experiment, it makes the central point move in accordance with the overall repulsion of circle pixels group and pixel group angular correction in linear iterative way until the central point stops in the dot which overall repulsion from circle pixels group is zero. That dot is the center point we want for. It is demonstrated that the acquired dot and component roundness using this method approximate the results from traditional from non-contact measurement. The proposed method can be applied in measuring roundness in practice. Furthermore, it contributes to the future research of roundness measurement from a new perspective and innovative method.
image processing; roundness measuring; mutex balance
1001-2265(2017)01-0105-04
10.13462/j.cnki.mmtamt.2017.01.029
2016-07-24;
2016-08-11
任晟德(1992—),男,安徽利辛人,广西大学硕士研究生,研究方向为图像测量,(E-mail)605057822@qq.com;通讯作者:韦衡冰(1968—),女,广西容县人,梧州学院副教授,研究方向为零件结构设计与数字化建模设计,(E-mail)519256379@qq.com。
TH166;TG506
A

