Pythagorean-Hodograph曲线插补及其G代码编程的实现

徐佰温，唐 伟

(山东大学 机械工程学院，济南 250061)

Pythagorean-Hodograph曲线插补及其G代码编程的实现

徐佰温，唐 伟

(山东大学 机械工程学院，济南 250061)

对Pythagorean-Hodograph(PH)曲线与数控加工相关的优点进行了研究，给出了PH曲线的构造方法，分析了PH曲线插补技术和其G代码编程的必要性和可行性，在传统G代码编程的基础上，介绍了一种PH曲线插补G代码编程实现的方法，编写了两个PH曲线插补G代码程序，可以看出该G代码编程可以和直线或圆弧插补G代码混合使用，扩充了传统G代码的使用范围，和通常的直线或圆弧分段逼近插补相比，其在精确性、高效性、传输数据量、灵活性方面具有明显的优势，为开发具有PH样条插补功能的数控系统提供了参考。

PH曲线；G 代码；CNC 插补

0 引言

在计算机数控系统中，复杂曲线曲面零件加工一直是研究的重点，样条曲线插补算法是高性能数控系统实现复杂轨迹生成的重要基础[1]。中低端数控机床大多仅具有直线和圆弧插补功能，其编程量大，加工精度低；高档数控机床通常具有样条插补功能，但也存在一些不足。现广泛使用的NURBS和B样条曲线插补有两个最基本的限制[2]：①刀心轨迹为非有理的，在CAD系统中需近似处理；②进给速度沿曲线的弧长不能精确计算。在高精数控加工中，易影响加工质量。而PH曲线的出现，完美的解决了上述不足。

PH曲线是一类特殊的构造曲线，可看作满足特定条件的Bézier曲线，由于具有了特别的代数结构形式，使得它具有一般自由曲线不可比拟的优点。在数控加工中，PH曲线的弧长和偏置曲线可被精确计算，能够准确方便的实现刀具半径补偿。在不同的加工场合，可根据需要选择不同进给速度函数，实现恒速或变速下的实时插补处理，国内一些高校对此进行了各自的研究[3-6]。

PH曲线可以和现存CAD系统的Bézier /B样条兼容，如果PH曲线插补的G代码程序可以和传统的G代码配合使用，则可以极大扩展G代码程序的使用范围。

1 Pythagorean-hodograph曲线

PH曲线是一种特殊的构造曲线，由美国学者R.T.Farouki[7]于1990年提出。

1.1 定义

对一条多项式参数曲线 r(ξ)=(x(ξ),y(ξ))，如果存在一个多项式σ(ξ)，使得

x′2(ξ)+y′2(ξ)=σ2(ξ)

(1)

则称r(ξ)为PH曲线。

其中多项式参数曲线的参数导数分量满足：

x′(ξ)=w(ξ)(u2(ξ)-v2(ξ))
y′(ξ)=2w(ξ)u(ξ)v(ξ)

(2)

w(ζ)、u(ζ)、v(ζ)为关于ζ的实多项式。

PH曲线由于满足(1)式这种特殊的代数结构形式，随后逐步被广泛应用于自由曲线曲面加工中的刀具轨迹规划，机器人的路径规划，汽车外形设计，实体造型和图形学等各个领域中[8]。

1.2 构造方法

根据PH曲线的定义，利用Bézier伯恩斯坦系数可求出u(ζ)和v(ζ)，则PH曲线即可确定。3次PH曲线不能实现C2的插值，没有拐点，在实际应用中受到很多限制。5次PH曲线具备普通三次多项式曲线的设计能力，可实现任意端点及其导数的Hermite插值，实际应用中较多。9次PH曲线的计算量较大，适用于特殊工业设计场合，如凸轮设计中。

下面以五次PH曲线的构造为例说明。

设PH曲线的次数为λ+2u+1

其中：

λ=deg(w(ξ)),u=max{deg(u(ξ)),deg(v(ξ))}

构造五次PH曲线时，u(ζ)和v(ζ)的次数为2，其Bernstein-Bézier形式表示为：

u(ξ)=u0(1-ξ)2+2u1(1-ξ)ξ+u2ξ2
v(ξ)=v0(1-ξ)2+2v1(1-ξ)ξ+v2ξ2

代入PH曲线的定义式，求得控制顶点[9]:

其中，p0为任意已知点。

则五次PH-Bézier曲线可表示为：

p(ξ)=p0b0.5(ξ)+p1b1.5(ξ)+p2b2.5(ξ)+p3b3.5(ξ)+p4b4.5(ξ)+p5b5.5(ξ)，可简写为：

式中，B为五次Bemstein系数。参数速度为：

其Bernstein系数为：

弧长多项式表示为：

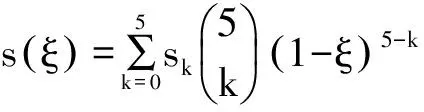
其Bernstein系数为：

s0=0

取ε∈[0,1]时，它的总弧长s为：

2 PH曲线插补

通常是将ξ(t)在t=(k-1)Δt处做泰勒级数展开，得：

公式右边都是在ξ=ξk-1点取值。

以最简单的恒速插补为例，说明求参数值的方法。

对于恒速插补，设：

V=V0，s(ξk)=kΔs0,Δs0=V0Δt

可由牛顿迭代法求出参数ξk

上式中，初始值为：

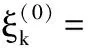
其中,σ(ξk-1)是前一步的收敛值。

3 PH曲线G代码

G代码，又称G编程语言，是最为广泛使用的NC编程语言，是使机床或数控系统建立起某种加工方式的指令[10]。主要在计算机辅助制造中用于控制自动机床。PH曲线与现存的CAD系统的Bézier/B样条曲线兼容，为PH曲线插补提供了可行性。传统G代码程序段结构清晰，方便灵巧，易于理解使用。为PH曲线使用G代码编程提供了良好的基础。

PH曲线伯恩斯坦系数转换的计算过程由CAD系统完成，PH曲线的次数、终点坐标、伯恩斯坦系数等信息，在编写G代码程序段中指定。

根据我国JB/T3208—1999《数控机床穿孔带程序段格式中的准备功能G和辅助功能M代码》，代码G05暂未指定功能，这里采用G05程序块中的字指定了PH曲线的几何信息和进给速度，见表1。

表1 PH曲线G代码坐标字的地址符含义

对部分程序字进一步的说明如下：

A,B,C,D,E：用于定义PH曲线的形状，若H为5，用到A，B，C三个数值；若H为9，需要用到A,B,C,D,E五个数值。P,Q,R,S,T用法与之相同。

F：指定进给速度函数的形式；

U,V,W:给出不同进给速度形式下的相关值。如：

F0:恒速进给，U速度值。

F1:进给速度与弧长成线性关系，U起点速度，V终点速度。

F2:进给速度与弧长成二次多项式关系，U起点速度，V终点速度。

F3:恒定材料去除率进给，U标称进给速度，V刀具半径，W切削深度。

F4:沿某一偏置曲线的恒速进给，U速度值，V偏置距离。

4 工件程序实例

PH曲线G代码可以和通常的直线圆弧插补G代码混合使用，以下举两个工件加工的例子来说明PH曲线G代码的紧凑灵活性。例子中的坐标值为十进制，单位为BLU(基本长度单位)，进给速度值单位为BLU/分钟。这里取1BLU=0.01mm。多项式u(ζ)、v(ζ)系数为十进制，保留三位小数以确保精度。假定工件的起始位置在(0,0)。

4.1 五次PH曲线变速进给

以下为5次PH曲线G代码段，进给速度样式为3。

N05 G05 F3 U30000 V635 W476

N10 G05 H5 X5080 Y0

N15 G05 A130.712 B-51.811 C138.385

N20 G05 P-69.955 Q128.872 R-29.367

N05程序块中的“F3”表示按照恒定材料去除率进给，标称进给速度U=30000BLU/min(5mm/s)，刀具半径V=635BLU(6.35mm)，切削深度W=476BLU(4.76mm)。N10程序块中“H5”表示为5次PH曲线，“X5080 Y0”表示终点坐标为(5080,0)。N15程序块中A，B，C为u(ζ)的伯恩斯坦系数。N20程序块中P，Q，R为v(ζ)的伯恩斯坦系数。

图1 实例：恒定材料去除率进给，上图为刀具运动轨迹，下图为实际进给速度

从图1可以看出，实际进给速度随加工轨迹的曲率的变化而自动改变，凸起的部分进给速度增加，而凹陷的部分进给速度会放慢，以达到恒材料去除率切削的目的。其它进给速度函数形式，可以通过改变F后面的数值来实现，如：

N05 G05 F1 U24000 V36000

表示进给速度为弧长的线性函数，进给速度由4mm/s线性增加至6mm/s。

4.2 PH曲线凸轮设计

PH曲线插补在设计和制造凸轮方面体现了巨大的优势。对于一个“驻留—上升—驻留—返回”形式的平面凸轮，凸轮的分度曲线由两段指定半径和跨越角度的圆弧，以及以某种方式连接它们的两段光滑曲线构成；该光滑曲线可采用9次PH曲线实现[11]。

图2 凸轮分度曲线组成

假设图2所示为凸轮分度曲线，它是实际的凸轮形状偏移一个从动件半径距离的偏置曲线。这里假设刀具半径等于从动件半径，则这里的分度曲线和希望的刀具路径重合。工件程序路径包含两段9次PH曲线(上升和返回弧)和4段圆弧(考虑到象限的问题，两驻留弧各分为两段)。

N05 G03 X2694 Y1116 I0 J3810 F24000

N10 G05 H9 X1796 Y5606 F0 U24000

N15 G05 A68.432 B78.556 C12.213 D36.348 E23.463

N20 G05 P28.345 Q46.970 R81.956 S58.111 T56.645

N25 G03 X0 Y6350 I1796 J1796

N30 G03 X-1796 Y5606 I0 J2540

N35 G05 H9 X-2694 Y1116

N40 G05 A-23.463 B-36.348 C-12.213 D-78.556 E-68.432

N45 G05 P56.645 Q58.111 R81.956 S46.970 T28.345

N50 G03 X0 Y0 I2694 J2694

这里特别需要提出的是：PH曲线凸轮及其分度曲线都是有理的，可以精确表示，从而克服了G代码中用直线或圆弧近似逼近表示的不足，既减少了编程工作量，又提高了加工精度。

5 结束语

PH曲线由于其特殊的结构形式，具有一系列与数控加工相关的优点，为开发具有PH样条插补功能的数控系统提供了必要性和可行性。在传统G代码编程的基础上，本文给出了PH样条插补G代码编程的方法，从两个实例可以看出，其具有紧凑灵活，简洁高效的特点，为开发PH样条插补功能的数控系统，提供了一些参考。

[1] 王允森，盖荣丽，孙一兰，等.基于牛顿迭代法的NURBS曲线插补算法[J].组合机床与自动化加工技术,2013(4)：17.

[2] Rida T Farouki, Jairam Manjunathaiah, Guo-Feng Yuan. International Journal of Machine Tools & Manufacture[J].1999,39: 123-142.

[3] 郭扬清.基于PH曲线的速度规划和误差估算方法的研究[D]. 哈尔滨:哈尔滨工业大学，2012.

[4] 龚志丹.PH曲线运动轨迹规划算法的研究与实现[D]. 哈尔滨:哈尔滨工业大学，2012.

[5] 蔡志娟.基于PH样条的五轴数控插补技术研究[D]. 哈尔滨:哈尔滨工业大学，2010.

[6] 王磊.Pythagorean Hodograph曲线及其插补技术的研究[D].济南:山东大学,2009.

[7] Rida T Farouki, Sakkalis T. Pythagorean Hodograph[J].IBM Journal of Research and Development,1990,34(5):736-752.

[8] 王国瑾，汪国昭，郑建民.计算机辅助几何设计[M].北京：高等教育出版社，2001.

[9] 马元魁. Pythagorean-Hodograph曲线的理论及应用研究[D].西安:西北大学，2005.

[10] 赵玉刚，宋现春.数控技术[M].北京：机械工业出版社，2003.

[11] R T Farouki, S Jee, J Manjunathaiah. Design of rational cam profiles with Pythagorean-Hodograph curves[J]. Mechanism and Machine Theory, 1998,33:669-682.

(编辑 李秀敏)

Pythagorean-hodograph Curves Interpolation and Associated G Codes Programming Implementation

XU Bai-wen,TANG Wei

(School of Mechanical Engineering, Shandong University, Jinan 250061, China)

The advantages of the Pythagorean-Hodograph(PH) curve associated with CNC machining is discussed, the construction method of PH curve is given. We analyze the PH curve interpolation technology and the necessity and fesibility of its G code programming. Based on the traditional G code programming, we introduce a method of PH curve interpolation G code programming, then write two PH curve interpolation G code programs for example, It can be seen that the proposed codes are compatible with ‘ordinary’ G codes, and can be regarded as its extension. Compared to the customary approach of using piecewise-linear/circular approximations, The above technologies and methods offer significant improvement in the accuracy, efficiency, data volume, and flexibility of the part programming and machining for free-form shapes, and may provide a reference for the development of the CNC system with the function of PH curve interpolation.

pythagorean-hodograph curves; G codes; CNC interpolators

1001-2265(2017)01-0102-03

10.13462/j.cnki.mmtamt.2017.01.028

2016-03-08

徐佰温(1983—)，男，山东聊城人，山东大学硕士研究生，研究方向为智能制造系统与数控技术，(E-mail)sdu200@163.com；通讯 作者：唐伟(1962—)，男，济南人，山东大学机械工程学院副教授，研究方向为数控技术和逆向工程，(E-mail)tangw@sdu.edu.cn。

TH166；TG659

A