基于NURBS插补算法的汽轮机叶片数控加工*

乐 英,王 颖

(华北电力大学 能源动力与机械工程学院，河北 保定 071000)

基于NURBS插补算法的汽轮机叶片数控加工*

乐 英,王 颖

(华北电力大学 能源动力与机械工程学院，河北 保定 071000)

为了提高汽轮机叶片的加工精度，文章通过分析汽轮机叶片的结构特点，采用一种NURBS曲线插补算法对其进行插补仿真。文章所采用算法由两部分组成：速度规划和参数计算。首先速度规划采用简化的五段S曲线加减速控制方法，保证了叶片在高速加工过程中加速度的连续，使机床运行平稳，然后利用牛顿迭代法来计算插补参数，得到更精确的插补参数，进一步提高了叶片的加工精度和加工速度。汽轮机叶片的插补仿真表明，该算法有高的稳定性和运算精度，并且使机床振动减小，速度波动小，保证了叶片的高质量加工。

汽轮机叶片；NURBS插补算法；五段S曲线加减速控制；牛顿迭代法

0 前言

汽轮机叶片的结构设计复杂，是一种典型的复杂自由曲面，是汽轮机中的关键部件，其加工质量直接影响到机组的运行效率和可靠性[1]。传统的数控加工系统，一般采用很多小的离散化的线段或者圆弧逼近曲线，这种方法会造成曲线轮廓不平滑，造成进给速度的不连续和波动，从而破坏工件表面的光滑性，而且大量的程序增加了CAD/CAM和计算机数控系统之间的通讯负担，影响插补的实时性。

目前，研究NURBS插补算法的国内外学者较多。Bedi[2]提出均匀参数插补算法，将参数增量视为常数，首次实现了NURBS曲线的实时直接插补。Shipital和Yang[3-4]分别采用一阶和二阶泰勒展开式，应用泰勒展开法计算插补参数使参数曲线直接插补应用在实践加工中成为可能，实现了恒定的进给速度插补，提高了计算精度，减小了速度波动。任杰青[5]等提出基于预估误差补偿的NURBS曲线预估-校正插补算法，降低了运算的复杂度并且利用基于割线法的校正公式减少了迭代计算的次数，进一步提高了计算精度。孙海洋[6]等在研究了参数曲线的数控插补原理后，发现一些直接插补算法的局限性，提出了利用牛顿迭代法计算插补参数，减小了进给速度波动，但是参数初值的计算相当复杂。上述这些算法都没有考虑加减速过程中的速度、加速度的变化，难以保证插补精度。Nam[7]等在考虑了加速度的约束之后，提出了一种限制加加速度的加减速控制方法，有效控制了轮廓误差，但是这种方法的实现比较复杂。周德胜[8]等全面考虑了弓高误差和法向加速度等参数的影响，提出一种基于NURBS曲线插补的五段S曲线加减速方法，解决了减速点预测的困难，实时性较好。潘海鸿[9]等提出一种七段式非对称S曲线加减速控制方法，考虑了工程应用的实际问题，提高了加工速度，但是计算复杂。

上述算法大多是应用在自由曲线曲面上，本文以汽轮机叶片为研究对象，根据汽轮机叶片的结构特点，对其采用NURBS曲线插补算法，该算法首先进行速度规划，速度规划采用简化的五段S曲线加减速控制算法，然后进行参数计算，参数计算利用牛顿迭代法，迭代初值采用简单线性递推方程计算。对汽轮机叶片截面的仿真结果表明，汽轮机叶片采用该算法进行插补保证了速度和加速度的连续，加加速度实现了有界变化，从而使得机床运行平稳，叶片的插补精度得到了提高，进给速度波动限制在理想范围内，进一步提高了叶片的加工质量。

1 NURBS曲线插补

一条k次NURBS曲线的表达式为[10-11]：

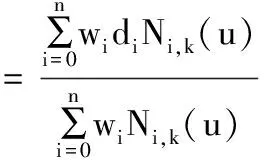
(1)

其中,wi(i=0,1,2,…,n)称为权或权因子(weights)。di(i=0,1,2,…,n)为控制顶点，与权因子wi(i=0,1,2,…,n)一一对应，顺序相连形成控制多边形。Ni,k(u)是由节点矢量U=[u0,u1,…,un+k+2]按德布尔-考克斯递推公式(2)推导的k次规范B样条基函数。

(2)

NURBS插补主要用弦线逼近弧线，这种逼近会造成实际进给速度与理想进给速度之间存在差异，从而导致速度波动，速度波动的大小采用δi表示，如公式(3)所示[12]：

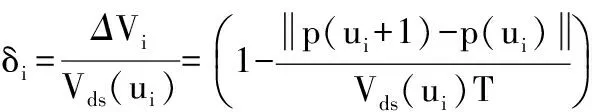
(3)

2 速度规划算法

2.1NURBS曲线自适应速度调整

在实时插补过程中，弓高误差、进给速度以及曲率半径之间的关系，采用如图1所示的方法进行计算：

图1 利用圆弧计算弦高误差示意图

ρi为u=ui处的曲率半径。弓高误差的计算如下式所示：

(4)

由最大弓高误差ER限定下的进给速度V(ui)为：

(5)

式(5)表明进给速度V(ui)与弓高误差ER和曲率半径ρi有关，其变化关系如下：

(6)

其中，F为编程进给速度。

2.2 五段S曲线加减速规划

速度的自适应调整可以得到满足精度要求的速度，但在曲线曲率半径变化较大的区域，比如曲率半径较小的区域，速度变化较大，可能会超出机床的加减速能力，对机床产生冲击[13]。

为调整小曲率半径区域曲线进给速度，使得加速度和加加速度实现连续有界变化，在曲线曲率尖角处采用五段S曲线加减速控制方法。

五段S曲线加减速控制算法将速度规划分为加加速段、减加速段、匀速段、加减速段和减减速段五个阶段。以减速段为例：

假设t=0时为减速过程的开始时刻，Vs为起始速度，Ve为终止速度，A为最大加速度，J为最大加加速度。

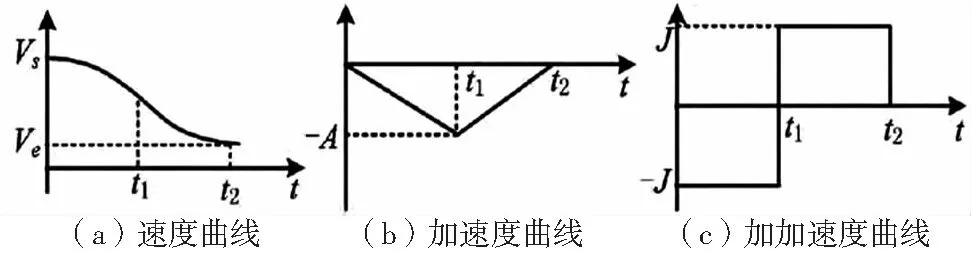
图2 五段S曲线加速度控制方法减速过程的速度、加速度和加加速度曲线

从图2可以看出，加减速阶段的速度方程曲线为:

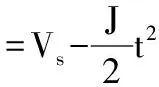
(7)

当t=t1时，A1(t1)=-Jt1=-A，有：

(8)

减速阶段的速度方程为：

(9)

由于整条速度曲线是连续的，有：

V1(t)=V2(t)

(10)

将式(7)～(9)代入式(10)可得：

(11)

设减速阶段的速度变化量为ΔV，即ΔV=Ve-Vs,当:

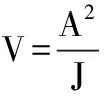
(12)

则机床加工的加速度和加加速度能够达到最大值。若

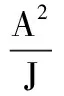
(13)

则机床加工的加速度不能达到最大值A，设此时达到的加速度值为Ai，由式(11)可得：

(14)

如果

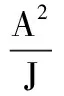
(15)

则机床加工的加加速度不能达到最大值J，设此时达到的加加速度值为Ji，由式(11)可得：

(16)

因此，在计算减速段的速度方程时，先根据式(12)～式(16)计算出减速阶段能达到的加速度和加加速度，然后根据公式(7)和式(9)得到减速段的方程。加速段过程的计算方法与减速段相同。

2.3 插补参数计算

为了减小截断误差，降低速度波动，本文采用牛顿迭代法计算插补参数：

(17)

式中，ui—当前插补参数;ui+1—下一个插补参数。

则问题转化为求ξ=ξ*，使得：F(ξ*) =0。

牛顿迭代法的计算原理如图3所示。

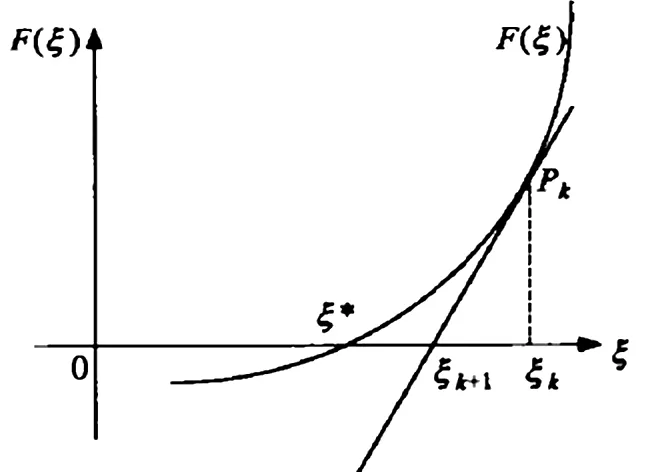
图3 牛顿迭代法示意图

设F(ξ)=0的近似根是ξk，过点Pk引切线，点Pk是曲线F(ξ)上横坐标为ξk的点，该切线与ξ轴的交点的横坐标为ξk+1，将ξk+1作为ξ*的新的近似值，因此可以得到迭代公式：

(18)

通常迭代法的迭代终止条件为：

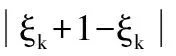
(19)

ε为迭代精度。在满足式(19)时，为了同时满足速度精度的要求，设置速度波动率δ的上限值作为迭代终止条件，并且规定了最大迭代次数的值K。

这里采用公式(20)所表示的线性递推法来计算迭代参数初值：

ui+1=2.5ui-2ui-1+0.5ui-2

(20)

为了避免出现插补反转，利用公式：

ui+1=2ui-ui-1=ui+(ui-ui-1)

(21)

式(21)可以保证ui+1>ui,不会出现插补反转的问题。

3 试验仿真

以某国产汽轮机组通流部分低压缸动叶片为例，叶身长为432mm，沿叶高方向有11个关键截面，如图4所示，各截面形状如图5所示。

图4 叶片横截面分布图

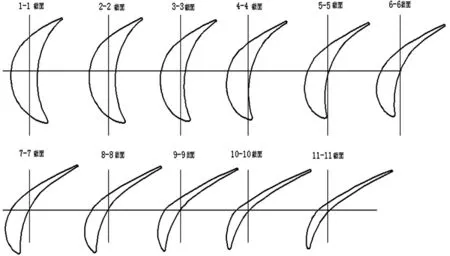
图5 叶片11个截面示意图

本文以叶片中间的截面为研究对象，叶片中间的截面采用NURBS拟合如图6所示。

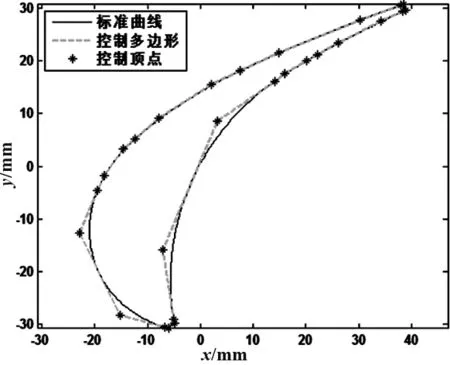
图6 叶片高度z=216mm的截面拟合图

从图中可以看出，叶片的曲率半径变化较大，进汽边和出汽边存在曲率半径很小的尖角。根据上图所示的叶片横截面，利用MATLAB软件采用上述方法对其进行NURBS曲线插补仿真。仿真时的编程速度F=100mm/s，插补周期T=0.001s，最大加速度A=0.008m/s2，最大加加速度J=0.004m/s3，允许的最大弓高误差ER=0.001μm，迭代精度E=10-6，最大迭代次数K=5，最大速度波动率Δ=2×10-4%。

仿真试验得到的弓高误差、速度曲线、加速度曲线及加加速度曲线分别如图7～图10所示。

图7 弓高误差图

图8 速度图

图9 加速度图

图10 加加速度图

仿真结果表明，本文所采用的插补算法使叶片所有插补点的弓高误差、进给速度、加速度和加加速度都控制在允许范围内，从而保证了叶片的加工精度满足要求，同时使得速度曲线实现平滑过渡，加速度曲线在加速段和减速段实现连续变化，并且加加速度实现有界变化，保证了叶片加工过程中机床的平稳运行，进一步提高了叶片的加工精度和加工效率。

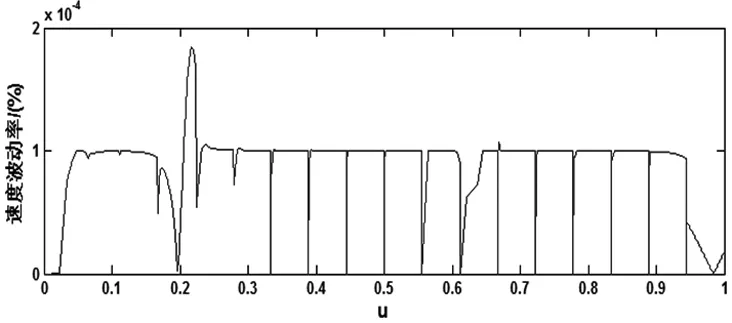
图11 速度波动率图

仿真结果得到的速度波动率如图11所示，从图中可以看出，本文采用牛顿迭代法进行插补参数的计算使得所有插补点的速度波动率均控制在10-4%量级范围内，说明相对于泰勒展开法计算所得的参数值更准确，速度更平稳，有效降低了速度波动。

综上所述，表明该算法稳定好，且运算精度高，减小了机床的振动，保证了加工过程的稳定性，大幅度提高了叶片的加工精度和加工效率。

4 结论

汽轮机叶片是汽轮机的重要部分，它的加工精度直接影响到汽轮机的工作效率，为了提高汽轮机叶片的加工质量，本文采用NURBS曲线插补算法对叶片截面进行插补仿真。算法分为两个部分：速度规划和参数计算。速度规划部分采用简化的5段S曲线加减速控制方法，而参数计算部分应用牛顿迭代法来计算插补参数，克服了传统方法利用泰勒公式进行计算计算量大且不准确的缺点。仿真试验结果表明，该算法能够提高叶片的加工效率，保证叶片插补过程中速度和加速度连续，从而提高了叶片的加工精度，并且使加加速度连续有界，避免了刀具在运行过程中对机床产生较大的冲击，保证机床可以平稳运行，有效减小了速度波动，从而满足叶片加工中高质量、高效率的加工要求。

[1] 乐英．提高汽轮机叶片加工效率的方法[J]．汽轮机技术，2012，54(3)：234-236，186．

[2] BEDI S，Ali S，QUAN N． Advanced interpolation techniques for CNC machines[J]．ASME Journal of Engineering for Industry，1993，S115(8)：329-336．

[3] SHIPIYAL NI M，KOREN Y，Lo C C．Real-time curve interpolation[J]．Computer-Aided Design， 1994，26(11)：832-838．

[4] Yang D C H，Kong T．Parametric interpolator for precision CNC machining parametric curves[J]．Computer-Aided Design．1994，26(3)：225-234．

[5] 任杰青，刘凯，赵东标．NURBS基于预估误差补偿的NURBS曲线插补算法[J]．机械科学与技术，2015，34(8)：1037-1041．

[6] 孙海洋，范大鹏，李玲．一种参数曲线实时数控插补计算新方法[J]．国防大学学报，2008，30(3)：122-127．

[7] NAM S H，YANG M Y．A study on a generalized parametric interpolator with real-time jerk-limited acceleration[J]．Computer-Aided Design，2004，36(1)：27-36．

[8] 周胜德，梁宏斌，乔宇．基于NURBS曲线插补的五段S曲线加减速控制方法研究[J]．组合机床与自动化加工技术，2011(4)：37-41．

[9] 潘海鸿，杨增启，陈琳，等．一种适用于前瞻的高精度7段式非对称S曲线加减速控制 [J]．机械科学与技术,2015，34(7)，1024-1030．

[10] 董海涛，潘海鸿，黄丽宇，等．一种优化的NURBS曲线插补算法[J]．计算机集成制造系统，2014，20(9)：2172-2177．

[11] 施法中．计算机辅助几何设计与非均匀有理B样条[M]．北京：北京航空航天大学出版社，1994．

[12] 王允森，盖荣丽，孙一兰，等．基于牛顿迭代法的NURBS曲线插补算法[J]．组合机床与自动化加工技术，2013(4)：13-17．

[13] 潘海鸿，杨微，陈琳，等．全程S曲线加减速控制的自适应分段NURBS曲线插补算法[J].中国机械工程，2010，21(2)：190-195．

(编辑 李秀敏)

NURBS Interpolation Algorithm for Turbine Blade in NC Machining

YUE Ying, WANG Ying

(School of Energy, Power and Mechanics Engineering, North China Electric Power University, Baoding Hebei 071000, China)

In order to improve the machining accuracy of turbine blade, a NURBS curve interpolation algorithm is used according to the structure features of the turbine blade，which included two parts of velocity planning and parameter calculating. First five phased S-curve acceleration and deceleration control method was adopted in velocity planning module．The accelerate speed is continuous when blade in high speed machining process using the method and the CNC machine runs smoothly．Then the interpolation parameters are calculated using Newton iterative method. It gets more accurate interpolation parameters，the machining precision and speed of the blade are more improved. The simulation test for interpolation of turbine blade shows that the algorithm has good stability, high computing precision. It can satisfy the requirements of the real-time interpolation，reduce machine tool vibration and limit the speed fluctuation in the real-time interpolation to the ideal level.

turbine blade；NURBS interpolation algorithm；five phased S-curve acceleration and deceleration control；Newton iterative method

1001-2265(2017)01-0078-04

10.13462/j.cnki.mmtamt.2017.01.021

2016-03-24；

2016-05-06

河北省自然科学基金项目(E2014502042)；中央高校基本科研业务费专项资金项目(11QJ61)

乐英(1971—)，女，河南信阳人，华北电力大学(保定)副教授，博士，研究方向为复杂曲面造型及数控加工的研究，(E-mail)yueying71@163.com。

TH165;TG659

A